Kaggle笔记:Porto Seguro’s Safe Driver Prediction(1)
Porto Seguro’s Safe Driver Prediction
这是Kaggle在9月30日开启的一个新的比赛,举办者是巴西最大的汽车与住房保险公司之一:Porto Seguro。该比赛要求参赛者根据汽车保单持有人的数据建立机器学习模型,分析该持有人是否会在次年提出索赔。比赛所提供的数据均已进行处理,由于数据特征没有实际意义,因此无法根据常识或业界知识简单地进行特征工程。
1.数据准备
首先,加载必要的包:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
import xgboost as xgb
import seaborn as sns
读入数据,需要注意的是,由于举办方将缺失值全部设置为-1,因此,在读入数据的时候,要添加参数na_values=-1,以重新确定缺失值的所在。
##读入数据,并取得特征:
train = pd.read_csv("D:\CZM\Kaggle\data\\train.csv",na_values = -1)
test = pd.read_csv("D:\CZM\Kaggle\data\\test.csv",na_values = -1)
2.探索性数据分析(EDA)-数据总体
本部分将对数据总体进行探索性分析,从中提取有用的总体信息。
2.1 从特征列名中提取信息
首先,查看一下数据的规模:
In [13]: len(train)
Out[13]: 595212
In [14]: len(train.columns)
Out[14]: 59
In [15]: len(test)
Out[15]: 892816
In [16]: len(test.columns)
Out[16]: 58
我们发现,训练集中有595212个样本,测试集有892816个样本,这是数据集的基本规模。
另外,测试集中有58列,训练集中有59列,这是由于测试集中不包含需要预测的目标变量。
接下来,查看一下测试集具体有哪些列:
In [34]: train.columns
Out[34]:
Index(['id', 'target', 'ps_ind_01', 'ps_ind_02_cat', 'ps_ind_03',
'ps_ind_04_cat', 'ps_ind_05_cat', 'ps_ind_06_bin', 'ps_ind_07_bin',
'ps_ind_08_bin', 'ps_ind_09_bin', 'ps_ind_10_bin', 'ps_ind_11_bin',
'ps_ind_12_bin', 'ps_ind_13_bin', 'ps_ind_14', 'ps_ind_15',
'ps_ind_16_bin', 'ps_ind_17_bin', 'ps_ind_18_bin', 'ps_reg_01',
'ps_reg_02', 'ps_reg_03', 'ps_car_01_cat', 'ps_car_02_cat',
'ps_car_03_cat', 'ps_car_04_cat', 'ps_car_05_cat', 'ps_car_06_cat',
'ps_car_07_cat', 'ps_car_08_cat', 'ps_car_09_cat', 'ps_car_10_cat',
'ps_car_11_cat', 'ps_car_11', 'ps_car_12', 'ps_car_13', 'ps_car_14',
'ps_car_15', 'ps_calc_01', 'ps_calc_02', 'ps_calc_03', 'ps_calc_04',
'ps_calc_05', 'ps_calc_06', 'ps_calc_07', 'ps_calc_08', 'ps_calc_09',
'ps_calc_10', 'ps_calc_11', 'ps_calc_12', 'ps_calc_13', 'ps_calc_14',
'ps_calc_15_bin', 'ps_calc_16_bin', 'ps_calc_17_bin', 'ps_calc_18_bin',
'ps_calc_19_bin', 'ps_calc_20_bin'],
dtype='object')
这里显示出了train数据集的列名,根据以上内容以及比赛举办方提供的数据说明,我们能够提取出的信息如下:
- 除去作为唯一标识的ID列以及target列之外,特征列共有57列。
- 特征列的列名结构是统一的,共有被下划线分割开来的四层词缀:第一层词缀是所有特征列都有的ps,不需要关注;第二层词缀有ind、reg、car、calc四个类别;第三层词缀是单纯的编号;而第四层词缀有bin、cat两个种类,需要注意的是,不是所有的特征列都具有第四层词缀的。
- 根据举办方给出的数据说明,第四层词缀标注的是特征的变量类型,cat为多分类变量,bin为二分类变量,无词缀则属于连续或顺序变量;而第二层词缀则是变量名称,Ind是与司机个人相关的特征,reg是地区相关的特征,car是汽车相关的特征,calc则是其他通过计算或估计得到的特征。第三层词缀虽然官方没有明说,但应该是每个变量名称下的变量编号。
因此,我们可以根据特征名称,对所有特征列归类:
calccol = [];carcol = [];indcol = [];regcol = [];
col = train.columns;lencol = len(col)
for i in range(lencol):
st = col[i]
if st.find('car') != -1:
carcol.append(st)
else:
if st.find('calc')!= -1:
calccol.append(st)
else:
if st.find('ind')!= -1:
indcol.append(st)
else:
if st.find('reg')!= -1:
regcol.append(st)
##把每种类型的列归类,会有意义的
bincol = [];catcol = [];othercol = []
for i in range(lencol):
st = col[i]
if st.find('bin') != -1:
bincol.append(st)
else:
if st.find('cat') != -1:
catcol.append(st)
else:
if (st != 'target') and (st != 'id'):
othercol.append(st)
然后,对所有数据列的数据类型归纳为下表:
| 特征列名 | 特征名 | 特征后缀 | 变量类型 |
|---|---|---|---|
| ps_ind_01 | ind | 无 | 连续或顺序变量 |
| ps_ind_02_cat | ind | cat | 分类变量 |
| ps_ind_03 | ind | 无 | 连续或顺序变量 |
| ps_ind_04_cat | ind | cat | 分类变量 |
| ps_ind_05_cat | ind | cat | 分类变量 |
| ps_ind_06_bin | ind | bin | 0-1变量 |
| ps_ind_07_bin | ind | bin | 0-1变量 |
| ps_ind_08_bin | ind | bin | 0-1变量 |
| ps_ind_09_bin | ind | bin | 0-1变量 |
| ps_ind_10_bin | ind | bin | 0-1变量 |
| ps_ind_11_bin | ind | bin | 0-1变量 |
| ps_ind_12_bin | ind | bin | 0-1变量 |
| ps_ind_13_bin | ind | bin | 0-1变量 |
| ps_ind_14_bin | ind | bin | 0-1变量 |
| ps_ind_15_bin | ind | bin | 0-1变量 |
| ps_ind_16_bin | ind | bin | 0-1变量 |
| ps_ind_17_bin | ind | bin | 0-1变量 |
| ps_ind_18_bin | ind | bin | 0-1变量 |
| ps_car_01_cat | car | cat | 分类变量 |
| ps_car_02_cat | car | cat | 分类变量 |
| ps_car_03_cat | car | cat | 分类变量 |
| ps_car_04_cat | car | cat | 分类变量 |
| ps_car_05_cat | car | cat | 分类变量 |
| ps_car_06_cat | car | cat | 分类变量 |
| ps_car_07_cat | car | cat | 分类变量 |
| ps_car_08_cat | car | cat | 分类变量 |
| ps_car_09_cat | car | cat | 分类变量 |
| ps_car_10_cat | car | cat | 分类变量 |
| ps_car_11_cat | car | cat | 分类变量 |
| ps_car_11 | car | 无 | 连续或顺序变量 |
| ps_car_12 | car | 无 | 连续或顺序变量 |
| ps_car_13 | car | 无 | 连续或顺序变量 |
| ps_car_14 | car | 无 | 连续或顺序变量 |
| ps_car_15 | car | 无 | 连续或顺序变量 |
| ps_reg_01 | reg | 无 | 连续或顺序变量 |
| ps_reg_02 | reg | 无 | 连续或顺序变量 |
| ps_reg_03 | reg | 无 | 连续或顺序变量 |
| ps_calc_01 | calc | 无 | 连续或顺序变量 |
| ps_calc_02 | calc | 无 | 连续或顺序变量 |
| ps_calc_03 | calc | 无 | 连续或顺序变量 |
| ps_calc_04 | calc | 无 | 连续或顺序变量 |
| ps_calc_05 | calc | 无 | 连续或顺序变量 |
| ps_calc_06 | calc | 无 | 连续或顺序变量 |
| ps_calc_07 | calc | 无 | 连续或顺序变量 |
| ps_calc_08 | calc | 无 | 连续或顺序变量 |
| ps_calc_09 | calc | 无 | 连续或顺序变量 |
| ps_calc_10 | calc | 无 | 连续或顺序变量 |
| ps_calc_11 | calc | 无 | 连续或顺序变量 |
| ps_calc_12 | calc | 无 | 连续或顺序变量 |
| ps_calc_13 | calc | 无 | 连续或顺序变量 |
| ps_calc_14 | calc | 无 | 连续或顺序变量 |
| ps_calc_15_bin | calc | bin | 0-1变量 |
| ps_calc_16_bin | calc | bin | 0-1变量 |
| ps_calc_17_bin | calc | bin | 0-1变量 |
| ps_calc_18_bin | calc | bin | 0-1变量 |
| ps_calc_19_bin | calc | bin | 0-1变量 |
| ps_calc_20_bin | calc | bin | 0-1变量 |
从上述的表格中,我们可以获取的信息如下:
- ind列大多数是分类或0-1变量,只有少数无后缀的连续/顺序变量;car列只有分类变量和无后缀的连续/顺序变量;reg列全部为连续变量;calc列大多数是无后缀的连续/顺序变量,还有一些0-1变量。
- ps_car_11和ps_car_11_cat的编号是相同的,这是整个数据集中唯一出现编号相同的情况,可能这两列之间存在某种相关性,之后可以进一步分析。
- 另外,还有一个很重要的信息没有出现在表中:数据集中虽然有很多没有后缀(即并非二分类或者多分类变量)的列,但是这些列大多数的取值形式是0.0,1.0,2.0,…或者0.1,0.2,0.3,…等取值范围,只有car特征中的少数几列无后缀特征列不属于这种形式。我们不能判断这些变量属于顺序变量还是连续型变量,但是应该记住这一点,之后也要进一步分析。
2.2 缺失值分析
首先,我们需要对训练集和测试集分别判断数据中有哪些列存在缺失值:
In [76]: train.isnull().any()[train.isnull().any()]
Out[76]:
ps_ind_02_cat True
ps_ind_04_cat True
ps_ind_05_cat True
ps_reg_03 True
ps_car_01_cat True
ps_car_02_cat True
ps_car_03_cat True
ps_car_05_cat True
ps_car_07_cat True
ps_car_09_cat True
ps_car_11 True
ps_car_12 True
ps_car_14 True
dtype: bool
In [77]: test.isnull().any()[test.isnull().any()]
Out[77]:
ps_ind_02_cat True
ps_ind_04_cat True
ps_ind_05_cat True
ps_reg_03 True
ps_car_01_cat True
ps_car_02_cat True
ps_car_03_cat True
ps_car_05_cat True
ps_car_07_cat True
ps_car_09_cat True
ps_car_11 True
ps_car_14 True
dtype: bool
上述列出了存在缺失值的列,注意到ps_car_12只在训练集中有缺失值,测试集中是没有的,而这里出现的其他列,则在训练集与测试集中均出现缺失值。
为了进一步探讨缺失值的分布,可以使用Aleksey Bilogur制作的missingno包,对数据集中的缺失值进行可视化分析:
import missingno as msno
col_missing = train.isnull().any()[train.isnull().any()].index
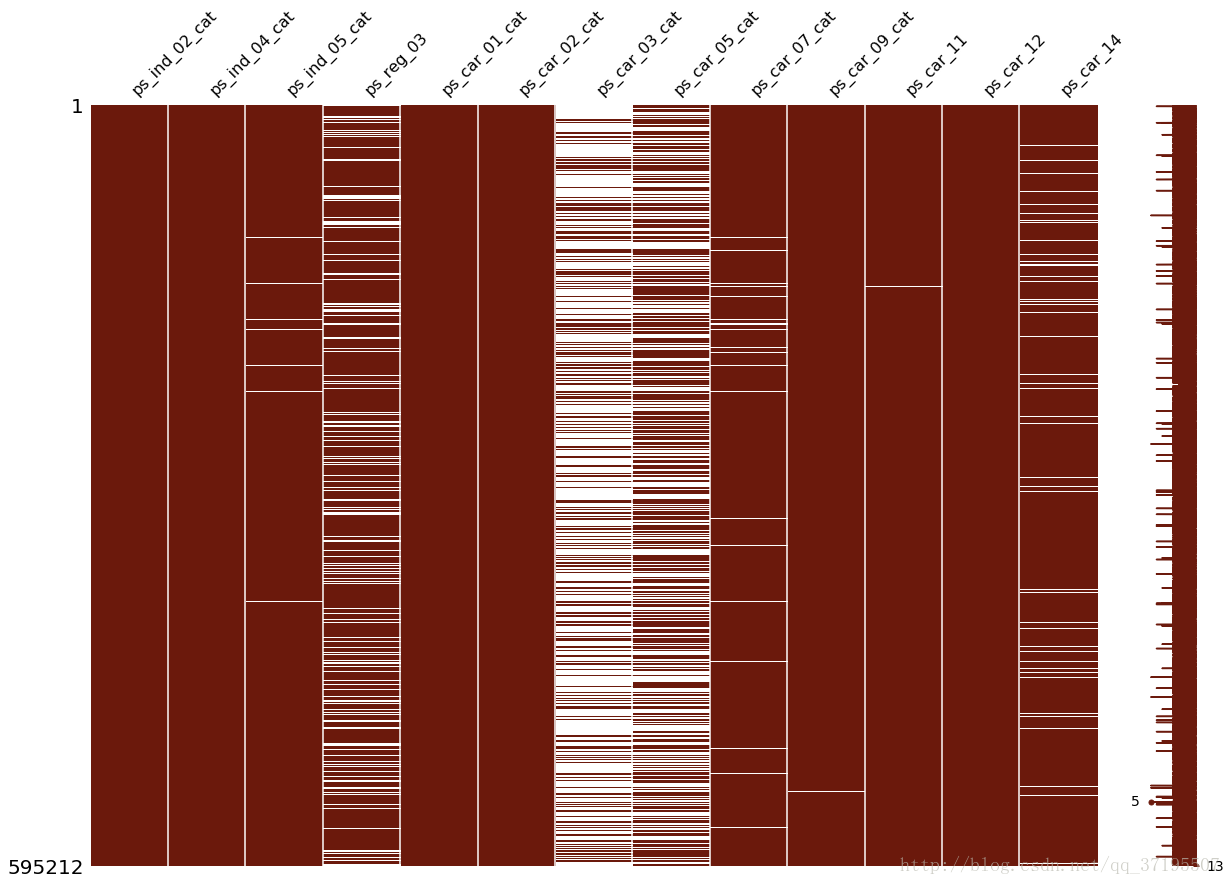
msno.matrix(df=train[col_missing], figsize=(20, 14), color=(0.42, 0.1, 0.05),)
上图是关于训练集缺失值分布的可视化结果,可以看到,出现缺失值最多的两个特征是ps_car_03_cat和ps_car_05_cat两列,其次则是ps_reg_03,再次ps_car_14,ps_car_07_cat和ps_ind_05,其他的特征,缺失值的数量就非常少了。
我们可以看一下训练集中,各列的缺失值数量:
In [121]: train[col_missing].apply(lambda c:len(c[c.isnull()])).sort_values()
Out[121]:
ps_car_12 1
ps_car_02_cat 5
ps_car_11 5
ps_ind_04_cat 83
ps_car_01_cat 107
ps_ind_02_cat 216
ps_car_09_cat 569
ps_ind_05_cat 5809
ps_car_07_cat 11489
ps_car_14 42620
ps_reg_03 107772
ps_car_05_cat 266551
ps_car_03_cat 411231
我们进一步确认,数据集中缺失值最多的是ps_car_03_cat列,缺失值多达四十万余条,可以说绝大多数样本这个特征都是缺失的。ps_car_05_cat次之,有26万余条,再次是缺失10万余条的ps_reg_03,然后是缺失值在一万以上的ps_car_14和ps_car_07_cat,其余的特征缺失值就较少了。
此外,出现缺失值的变量大多数都是分类变量,只有少数的连续或顺序变量,这也是值得注意的。如果考虑到ps_car_11和ps_car_12的缺失几乎可以忽略不计,那么实际上只有ps_car_14和ps_reg_03比较重要。
接下来,可以利用Missingno包中的heatmap函数,这个函数绘制的热图,可以呈现一个变量的缺失对另外的其他变量缺失情况所造成的影响:
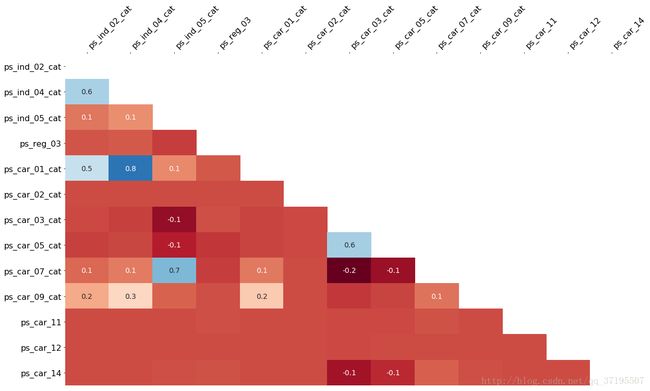
mano.heatmap(df=train[col_missing])
从上图中,我们发现:
- ps_ind_02_cat与ps_ind_04_cat、ps_car_01_cat,这三个变量的缺失情况在彼此之间的相关性很强。其中,ps_car_01_cat与ps_ind_04_cat的缺失情况相关性是所有系数里最高的。我们可以猜测,这三列之间具有一定的相关关系,使得一旦其中有一个变量出现缺失,其余两个变量的缺失与否也会受到影响。
- 此外,ps_car_07_cat和ps_ind_05_cat这两列的缺失情况之间也具有很强的相关性。
- ps_03_cat和ps_05_cat的缺失情况之间同样具有很高的相关性,但是如果考虑到这两列的缺失值都非常的多,就可以认为这是很理所当然的。
- 此外,我们也可以意识到,即使是不同变量名的特征之间也可能具有某种相关关系。
接下来,为了确认一下测试集中的缺失值是否具有与训练集接近的分布,同样对测试集绘制各个图形,并查看缺失值的数量:
In [127]: test[col_missing].apply(lambda c:len(c[c.isnull()])).sort_values()
Out[127]:
ps_car_12 0
ps_car_11 1
ps_car_02_cat 5
ps_ind_04_cat 145
ps_car_01_cat 160
ps_ind_02_cat 307
ps_car_09_cat 877
ps_ind_05_cat 8710
ps_car_07_cat 17331
ps_car_14 63805
ps_reg_03 161684
ps_car_05_cat 400359
ps_car_03_cat 616911
dtype: int64
可以看到,测试集中各列缺失值的数量关系与训练集较为接近。
msno.heatmap(df=test[col_missing])
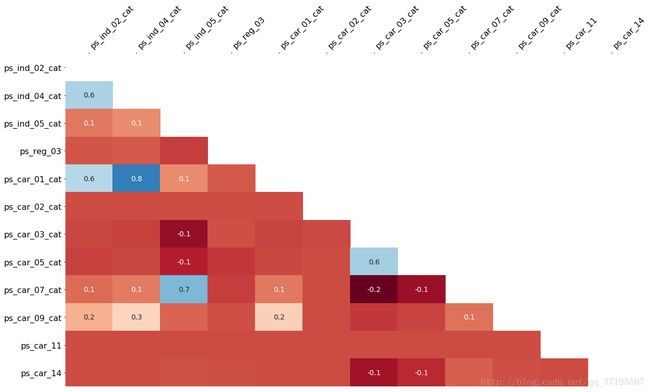
根据测试集的缺失值绘制的heatmap也与测试集十分接近,这说明训练集与测试集的缺失值分布是较为相似的,我们可以根据训练集中的缺失值情况,来对测试集进行分析和预测。
由于数据中的缺失值较多,且各列缺失情况之间存在一定的相互关系,所以这里暂时不对缺失值进行处理(删除或插补),而是会以存在缺失值的前提下继续分析数据。
2.3 target分析
这里,考察训练集中目标变量target的分布情况:
In [138]: target = train['target']
...: target.value_counts()
Out[138]:
0 573518
1 21694
Name: target, dtype: int64
可以看到,在所有595212个训练集样本中,只有21694个样本的目标变量是1,其余573518个样本的目标变量值都为0。说明这是一个非常不平衡的分类问题,在后续的分析与建模过程中,必须考虑到这一点。
2.4 相关系数分析
为了确认特征之间的线性相关性,通常我们会对各个连续特征计算它们相互之间的皮尔森相关系数,并列出相关矩阵。这里,我对所有属于连续或顺序变量以及二分类变量的特征计算相关矩阵,并利用seaborn模块进行可视化:
colormap = plt.cm.magma
plt.figure(figsize=(32,24))
plt.title(u'Pearson_bin_other', y=1.05, size=15)
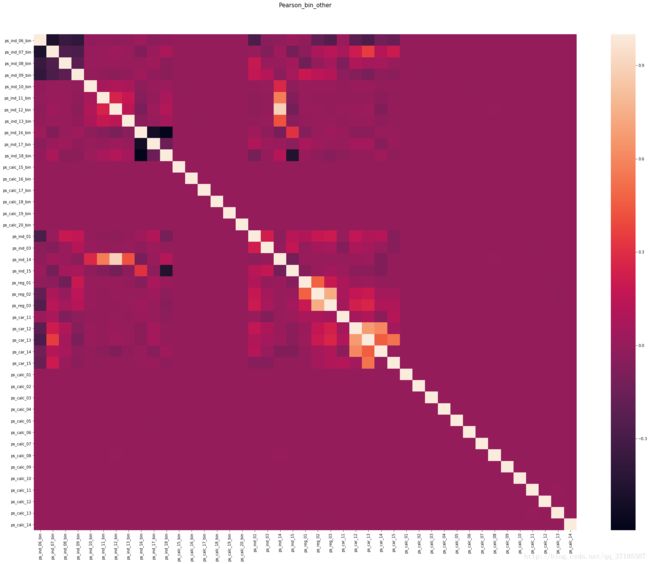
sns.heatmap(train[bincol+othercol].corr())
(如果觉得图片不够大,可以另开窗口打开后放大到100%)
这张图很大,看起来也很吃力,更重要的是,在进一步分析之前,我们可以对其进行优化并先提取显而易见的信息:非常明显的,所有的calc类特征,不论是否属于bin二分类变量,都与其他特征之间几乎不存在任何的相关性。
这一信息需要记住,并应用在后面的分析中。而现在,剔除所有名称含calc的特征后,也更换一下图片的颜色,重新绘制更容易看懂的相关系数图:
cmap = sns.diverging_palette(220, 10, as_cmap=True)
plt.figure(figsize=(32,24))
plt.title(u'Pearson_bin_other', y=1.05, size=15)
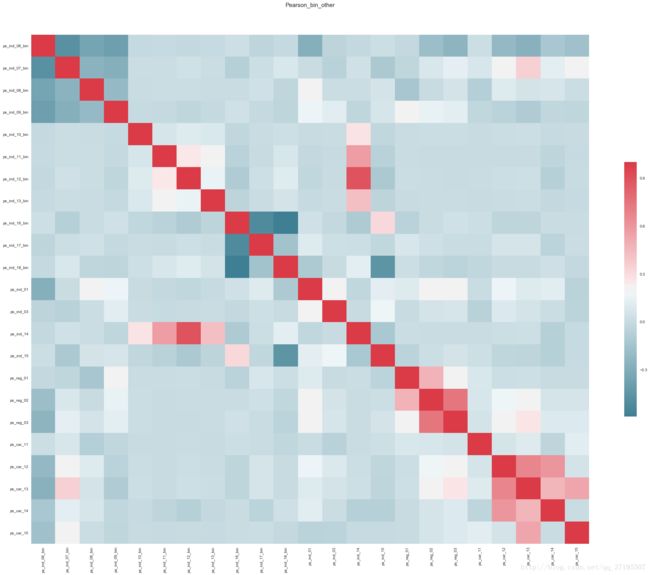
sns.heatmap(train[col_corr_nocalc].corr(),cmap = cmap,cbar_kws={"shrink": .5})
现在图片变得容易看懂得多,以下信息可以从图中提取出来:
- ps_ind_06_bin、ps_ind_07_ bin、ps_ind_08_bin、ps_ind_09_ bin这四列,相互之间均具有较强的负相关。
- ps_ind_16_bin、ps_ind_17_bin、ps_ind_18_bin这三列,相互之间均具有较强的负相关。
- ps_reg_02分别与ps_reg_01、ps_reg_03之间存在较强的正相关,ps_reg_01与ps_reg_03之间的相关程度相对低一些。
- ps_car_12、ps_car_13、ps_car_14、ps_car_15这四列,相互之间均具有较强的正相关。
- ps_ind_14与ps_ind_10_bin 、ps_ind_11_bin、ps_ind_12_bin、ps_ind_13_bin之间各自存在程度不同的正相关,其中ps_ind_14与ps_ind_12_bin之间的正相关性是最强的。而这些与ps_ind_14正相关的特征列彼此之间几乎不存在相关性。
- 此外,ps_ind_15和ps_ind_16_bin之间存在较强的负相关;ps_ind_15与ps_ind_16_bin之间也存在一定的正相关。
可以看到,较强的线性相关性都只存在于相同名类的特征之间(即ind与ind、car与car、reg与reg等),不同类型的特征之间几乎不存在较强的线性相关。此外,calc类的特征无论是彼此之间还是与其他名类的特征之间,都几乎不存在任何线性相关。
3.探索性数据分析(EDA)-特征分析
本部分将会对各个特征以及特征之间的关系进行详细分析,从中提取有用的信息。
3.1 二分类特征分析
首先,对所有后缀为“_bin”的二分类特征进行分析。
由于二分类特征的取值只能为0或1,因此,可以先采用层叠条形图,观察每个二分类变量取值的比例分布(由于前面已经确定二分类特征没有出现缺失值,所以不考虑缺失值)。
接下来的作图采用在线绘图库Plotly完成,Plotly是一个交互式可视化的第三方库,支持R、Python等语言,简单易用且可视化效果上佳。链接在此
len_train = len(train)
len_test = len(test)
##bin:
#层叠条形图:
import plotly.plotly as py
import plotly.graph_objs as go
##首先,获得bincol下每个col的0、1、缺失的数量
bin_zero_list = []
bin_one_list = []
for i in bincol:
temp = train[i].value_counts()
zero = temp[0]
one = temp[1]
nan = len_train - zero - one
bin_zero_list.append(zero)
bin_one_list.append(one)
trace_1 = go.Bar(
x = bincol,
y = bin_zero_list,
name = 'Zero Counts'
)
trace_2 = go.Bar(
x = bincol,
y = bin_one_list,
name = 'One Counts'
)
bin_plot_data = [trace_1,trace_2]
layout = go.Layout(
barmode = 'stack')
fig = go.Figure(data = bin_plot_data,layout = layout)
py.iplot(fig, filename='stacked-bar')
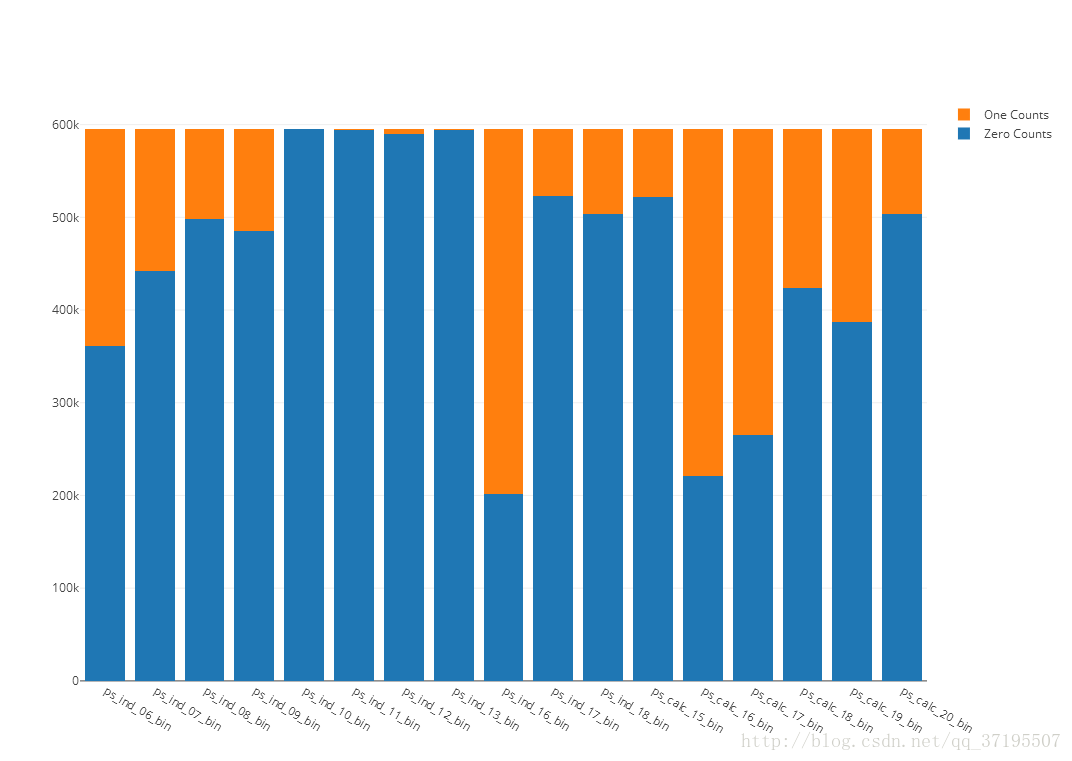
可以发现,几乎所有二分类特征的取值分布都不平衡,大多数的二分类特征取0的值远比取1的多,其中ps_ind_10_bin、ps_ind_11_bin、ps_ind_12_bin,ps_ind_13_bin这四个特征则几乎所有的取值都是0。这样的特征,可能对于预测几乎不会有帮助。
回忆起先前分析相关系数的时候存在这样的信息:ps_ind_14与ps_ind_10_bin 、ps_ind_11_bin、ps_ind_12_bin、ps_ind_13_bin之间各自存在程度不同的正相关。联系图中的信息,我们有必要提前确认一下ps_ind_14的取值分布:
In [257]: train.ps_ind_14.value_counts()
Out[257]:
0 588832
1 5495
2 744
3 136
4 5
Name: ps_ind_14, dtype: int64
可以看到,ps_ind_14的取值绝大多数都由0组成,在这样的情况下,ps_ind_14当然会与上述几个同样几乎绝大多数取值均为0的变量之间具有强相关性,我们可以判断这一相关性对于解决我们的问题是没有帮助的。
重新回到上述图的分析,我们还会发现ps_ind_16_bin、ps_calc_16_bin、ps_calc_17_bin这三列特征是取1的样本比取0的多,这和其他特征的趋势不太一样。而根据先前的相关系数分析,ps_ind_16与ps_ind_15之间是负相关的,我们可以看到ps_ind_15特征的情况是取0的样本数量比取1的样本多。
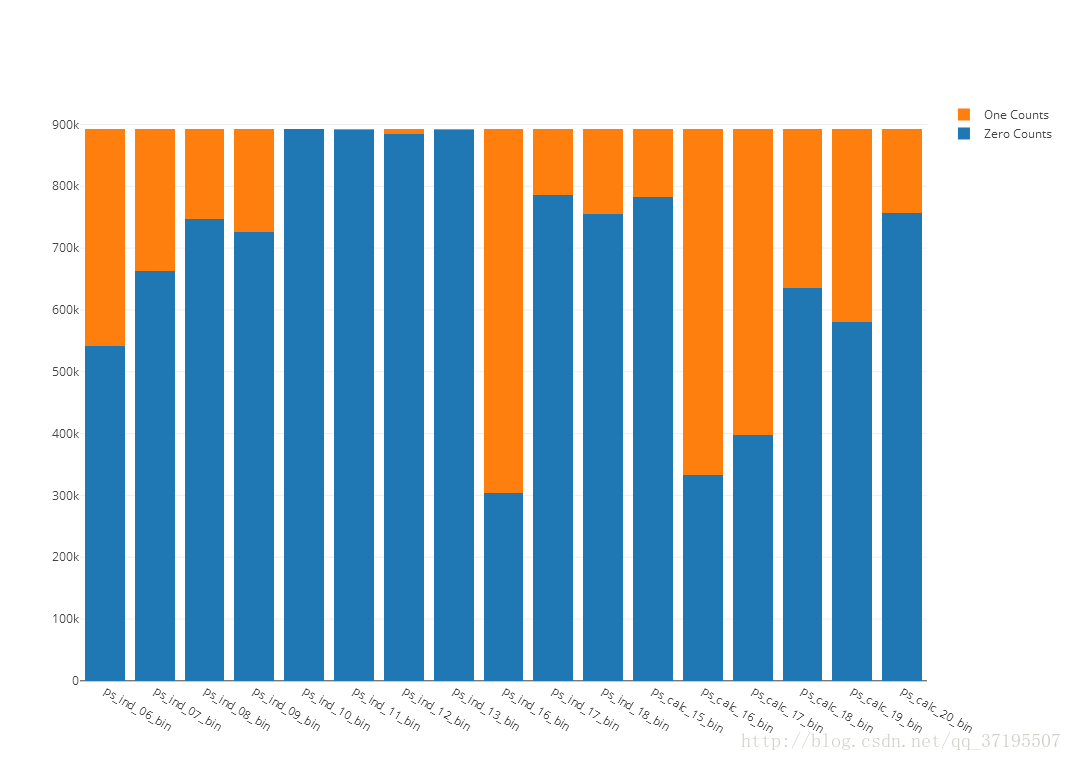
为了确定测试集中是否也如此分布,这里同样对测试集的二分类特征绘制相同的图形,代码略去,图形如下:
可以看到的是,测试集中的二分类变量取值分布与训练集中极为相似,不存在分布不同的问题。
接下来,我们还要观察这些变量与target变量之间的关系,为此,对每个二分类特征,分别计算特征取0与1时Target=1的概率:
train_1 = train[train.target == 1]
train_0 = train[train.target == 0]
len_train1 = len(train_1)
len_train0 = len(train_0)
k = 0
plt.figure(figsize=(30,20))
for x in bincol:
k = k+1
temp0 = train_0[x].value_counts()
bin_zero_t0 = temp0[0]
bin_one_t0 = temp0[1]
temp1 = train_1[x].value_counts()
bin_zero_t1 = temp1[0]
bin_one_t1 = temp1[1]
name_0 = 'feature:0'
name_1 = 'feature:1'
name = (name_0,name_1)
#zerolist = (bin_zero_t0/(bin_zero_t0+bin_zero_t1),bin_one_t0/(bin_one_t0+bin_one_t1))
onelist = (bin_zero_t1/(bin_zero_t0+bin_zero_t1),bin_one_t1/(bin_one_t0+bin_one_t1))
plt.subplot(4,5,k)
plt.ylabel('Proportion Of Target=1')
plt.title(x)
#plt.bar(name,zerolist,color = 'red',width = 0.8,label = 'target:zero')
plt.bar(name,onelist,width = 0.8,label = 'target:one')
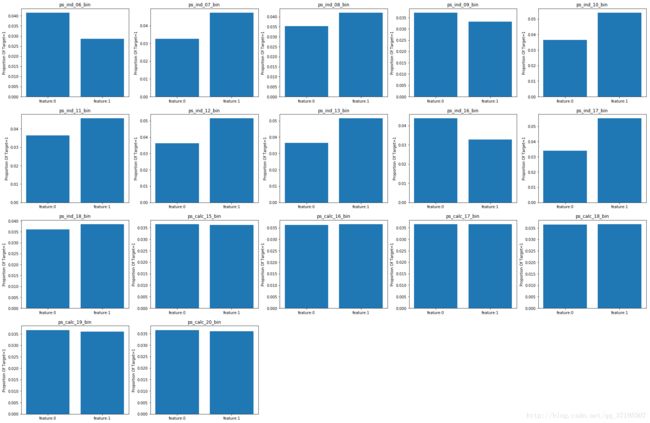
上图计算的是每个特征的不同取值下,目标变量Target的取值为1的概率,即Target=1这一事件关于每个二分类变量取值的条件似然概率。之所以选择这个指标来衡量Target的分布,是因为前述分析中我们知道Target是极不平衡的目标变量。
根据这一组图可以发现:数据集所有的二维变量中,大多数ind类的特征的取值都会对Target变量产生影响,根据这些变量的取值,Target=1的概率会有所变化;但是所有的calc类特征对Target都几乎没有影响。结合先前的分析中calc类特征与其他特征几乎不存在相关性这一点,可以猜测calc类特征很可能对于预测Target的任务没有帮助。
3.2 多分类特征分析
数据集中名字里含有“_cat”后缀的特征属于多分类变量特征,在数据集中存在14个多分类特征,下面对该部分特征进行分析。需要注意的是,由于这部分特征存在缺失值,因此本段把缺失值也作为一个类别参与分析。
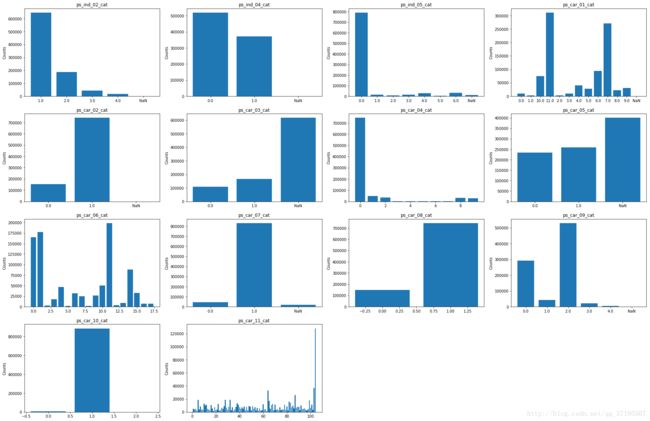
首先,对每个特征的取值分布画图:
##画每个cat特征的条形分布图:
k = 0
plt.figure(figsize=(30,20))
for x in catcol:
k = k+1
names = list(train[x].value_counts().index)
counts = list(train[x].value_counts().values)
if x in col_missing:
names.append('NaN')
counts.append(len_train - sum(counts))
plt.subplot(4,4,k)
plt.title(x)
plt.ylabel('Counts')
plt.bar(names,counts)
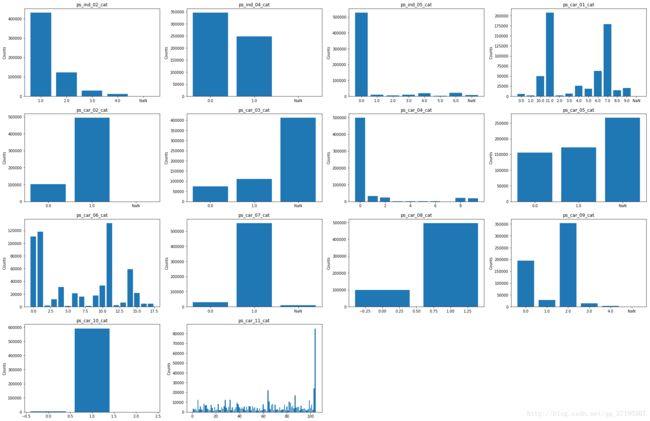
上述组图为每个特征的取值分布绘制了条形图,从这组图中我们可以获得的信息如下:
- 绝大多数分类特征的取值分布都是不平衡的,往往会出现少数的一个或几个取值频数极高,其余取值则只有很少的样本,这些特征值得继续关注。
- ps_car_11_cat的类别实在是太多了,或许可以猜测这其实是一个被误认为是分类变量的连续或顺序变量。这一推测并不是不可接受的,因为组图已经为我们展示出来了另一处特征变量类型误判:ps_car_08_cat以及ps_ind_04_cat实际上都属于二分类特征(不过,其中一个存在缺失值),却被数据提供方归入了多分类特征。
接下来,同样对测试集绘制相同的组图,观察测试集中多分类变量的取值分布是否与训练集有异:
能够看到测试集各个多分类变量的取值分布几乎和训练集的一模一样,也不存在分布不相同的问题。
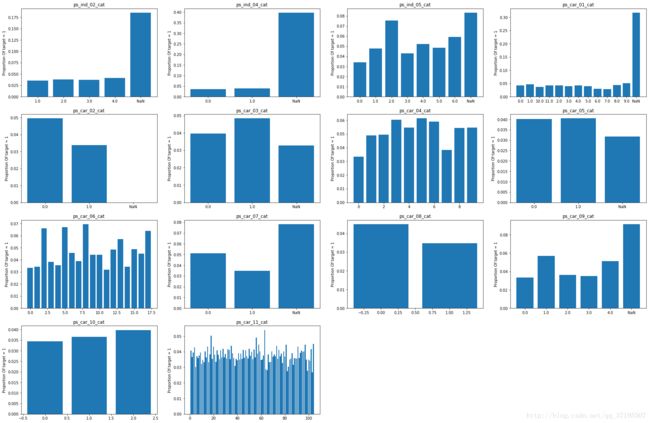
为了进一步分析多分类特征与target变量之间的关系,接下来计算每个特征的不同取值下,target=1的概率并作图:
上述组图表现出了各个多分类特征不同取值下Target=1的概率,这一组图片带给了我们非常重要的信息:在几乎所有出现了缺失值的特征中,绝大多数的缺失值都对Target变量的取值有非常大的影响!观察ps_ind_02_cat,这一特征缺失的情况下Target=1的概率远远超过了该特征其他任何取值,而对于ps_car_02_cat,缺失值意味着Target=0的概率几乎为0。
几乎所有特征的缺失值都带来了十分有用的信息,这意味着对于这些特征而言,缺失值所意味着的很可能并不是单纯的“数据遗漏”,而是同样作为多分类特征中一个特殊的“类别”而存在的。因此,对待这些多分类特征中的缺失值,将其视为一个单独的分类,显然比起用各种方法将其插补为其他分类更有意义。
3.3 顺序与连续特征分析
名称中不存在_cat或_bin后缀的特征被数据提供方归类为顺序或连续变量,由于这两种计量尺度存在一定的区别,因此,在对这类变量进行分析以前,首先要确认各个变量的取值范围:
In [185]: for x in othercol:
...: v = len(train[x].value_counts())
...: print (x+"'s kinds of value:",v)
ps_ind_01's kinds of value: 8
ps_ind_03's kinds of value: 12
ps_ind_14's kinds of value: 5
ps_ind_15's kinds of value: 14
ps_reg_01's kinds of value: 10
ps_reg_02's kinds of value: 19
ps_reg_03's kinds of value: 5012
ps_car_11's kinds of value: 4
ps_car_12's kinds of value: 183
ps_car_13's kinds of value: 70482
ps_car_14's kinds of value: 849
ps_car_15's kinds of value: 15
ps_calc_01's kinds of value: 10
ps_calc_02's kinds of value: 10
ps_calc_03's kinds of value: 10
ps_calc_04's kinds of value: 6
ps_calc_05's kinds of value: 7
ps_calc_06's kinds of value: 11
ps_calc_07's kinds of value: 10
ps_calc_08's kinds of value: 11
ps_calc_09's kinds of value: 8
ps_calc_10's kinds of value: 26
ps_calc_11's kinds of value: 20
ps_calc_12's kinds of value: 11
ps_calc_13's kinds of value: 14
ps_calc_14's kinds of value: 24
上述输出结果所列出来的是所有无后缀特征的变量取值种类数,我们可以看到,除了ps_reg_03、ps_car_12、ps_car_13、ps_car_14的取值总数非常多,应当属于连续变量特征之外,其他特征的可取值数都小于30:它们可能属于顺序变量,也可能属于连续的定距变量。无论如何,我们需要把这两种特征区分对待。
为此,将ps_reg_03、ps_car_12、ps_car_13、ps_car_14这四个特征归为连续变量,而其余的特征则归为顺序或定距变量:
conti_other = ['ps_reg_03','ps_car_12','ps_car_13','ps_car_14']
rankORint_other = [x for x in othercol if x not in conti_other]
接下来,我们对连续或顺序变量特征进行具体分析。
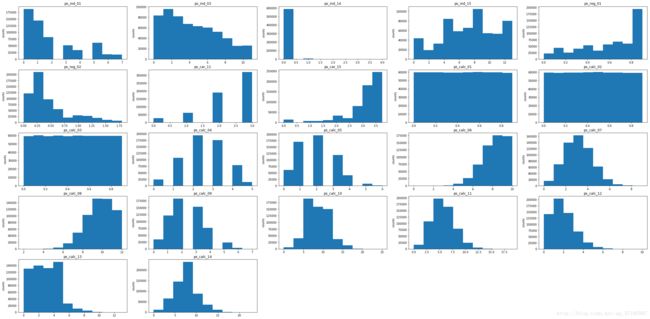
我们需要作图展示这些特征的本身的取值分布,首先,对所有的顺序或定距特征画直方图:
k = 0
plt.figure(figsize=(40,20))
for x in rankORint_other:
k = k+1
plt.subplot(5,5,k)
plt.title(x)
plt.ylabel('counts')
plt.hist(train[x].dropna())
从图中我们能够取得的信息如下:
- ps_ind_01,ps_reg_01,ps_car_15,ps_reg_02,ps_calc_06近似于长尾分布。
- ps_calc_04,ps_calc_07,ps_calc_05,ps_calc_09,ps_calc_11,ps_calc_14近似于正态分布。
- ps_calc_01,ps_calc_02,ps_calc_03属于均匀分布。
- ps_ind_01,ps_ind_03,ps_reg_02,ps_calc_12,ps_calc_13近似于右偏分布。
- ps_reg_01,ps_car_15,ps_calc_06,ps_calc_08近似于左偏分布。
从上面我们可以看到,近似正态分布和均匀分布的特征全部是calc类特征,而ind、car、reg特征的取值分布均是不平衡的。
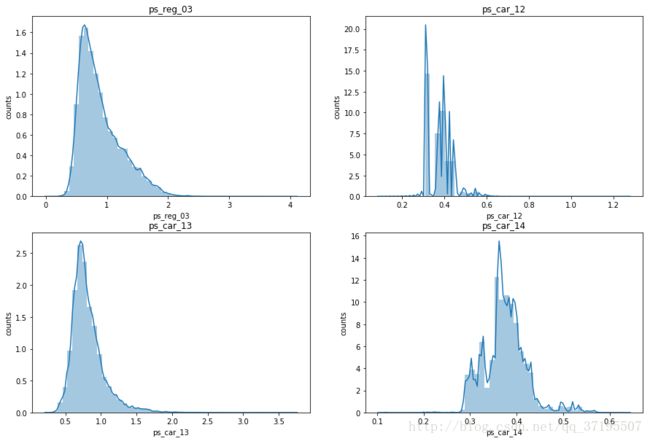
接下来,观察连续变量特征的直方图:
k = 0
plt.figure(figsize=(30,20))
for x in conti_other:
k = k+1
plt.subplot(1,4,k)
plt.title(x)
plt.ylabel('counts')
sns.distplot(train[x].dropna())
上述组图采用seaborn绘制了带密度函数曲线的直方图,使我们能够更加直观地确定各个特征变量的分布。我们可以发现,所有特征取值都有长尾倾向,ps_reg_02和ps_car_13的密度函数曲线较为平滑且右偏,ps_car_12和ps_car_14的分布则显得很不规则。
从上述分析中我们可以进一步发现,除了calc类之外,绝大多数连续与顺序特征的取值都是不平衡的,其直方图也不对称,而只有calc类的特征直方图中出现了近似正态分布和均匀分布的情况,即使不近似正态分布和均匀分布的部分,其取值也相较其他类型的特征更加平衡。
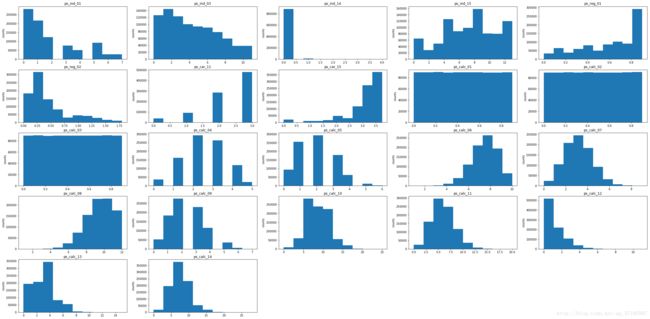
为了检验测试集中的特征分布是否与训练集一致,我们对测试集绘制同样的图形:
从测试集的直方图中我们发现,绝大多数的连续或顺序变量在训练集和测试集里的分布都是一致的,但是,ps_calc_06,ps_calc_12,ps_calc_13,ps_calc_14这四个特征在测试集与训练集中的取值分布是不同的,这些特征很可能无法对预测测试集的target变量起到作用,需要注意的是,这些特征全部都是calc类特征,而在此前的分析中,我们已经多次发现calc类特征缺少分析价值。
接下来我们要研究所有连续或顺序变量特征与Target变量之间的关系,首先,对顺序或等距特征画target=1关于特征取值似然概率的条形图:
train_rank = train[othercol].copy()
train_rank['target'] = train['target'].copy()
train_rank = train_rank.dropna()
train_rank01 = train_rank[train_rank.target == 1]
train_rank00 = train_rank[train_rank.target == 0]
train_rank_target = train_rank.target
len_train_rank01 = len(train_rank01)
len_train_rank00 = len(train_rank00)
k = 0
plt.figure(figsize=(30,30))
for x in rankORint_other:
k = k+1
names = list(train_rank[x].value_counts().index)
counts_0 = train_rank00[x].value_counts()[names]
counts_1 = train_rank01[x].value_counts()[names]
counts_0 = counts_0.replace(np.nan,0).values
counts_1 = counts_1.replace(np.nan,0).values
prop = counts_1/(counts_1+counts_0)
prop = list(prop)
plt.subplot(5,5,k)
plt.title(x)
plt.ylabel('Proportion Of target = 1')
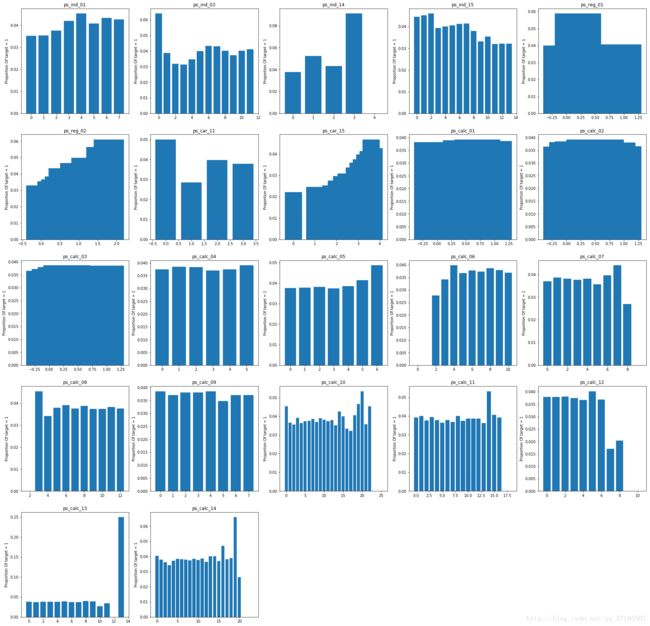
plt.bar(names,prop)
从上述的组图当中我们能获取以下信息:
- 在大多数特征中,Target=1的条件似然概率会根据特征的不同取值而有明显变化,比较明显的如在ps_ind_14中,特征取值为4意味着不存在target=1的样本,在ps_car_15、ps_calc_06、ps_calc_07、ps_calc_10、ps_calc_11、ps_calc_12、ps_calc_13中这种情况也有出现。需要注意的是又一次出现了大量的calc类特征。
- 然而ps_calc_01、ps_calc_02、ps_calc_03、ps_calc_04,ps_calc_09这几个特征的取值似乎几乎没有对Target变量造成影响,这已经不是这几个特征第一次表现出这样的无价值性了。
- ps_calc_13取值为13时Target=1的似然概率远远高过ps_calc_13取其他值,这是一个很重要的信息。虽然训练集和测试集中ps_calc_13的取值分布不同,但是ps_calc_13=13所占的比例在训练集与测试集中是接近的,应该单独拿出来考虑,同样的,对ps_calc_12、ps_calc_14也应这样考虑。
接下来,画Target取值关于四个连续特征取值分布的KDE密度曲线图:
k = 0
plt.figure(figsize=(15,15))
for x in conti_other:
k = k+1
plt.subplot(2,2,k)
sns.kdeplot(train_rank00[x])
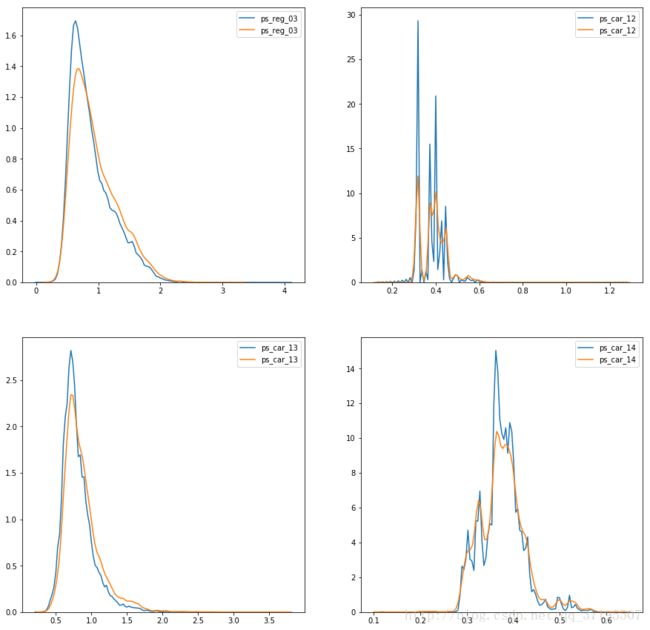
sns.kdeplot(train_rank01[x])
其中,蓝色的线是当target=0时特征的密度曲线,黄色的则是target=1时的密度曲线。
可以看到,对这几个特征而言,target=1意味着它们的密度曲线顶峰会低一些,局部最小点会高一些,曲线会平滑一些,但是大体来说,分布没有发生根本的改变。曲线幅度变化最大的是ps_car_12。
到此为止,我们对顺序或连续特征的取值分布分析基本完成,接下来,有4个连续或顺序特征存在缺失值,所以我们要对缺失值和Target变量之间的关系进行分析:
对于ps_car_12和ps_car_11,缺失值意味着target不会等于1,这看起来是很重要的信息,但是必须意识到,ps_car_12和ps_car_11在训练集中出现缺失值的个数分别是5和1,也就是说,缺失值在整个数据中只占了一个非常非常小的比例,而训练集的Target目标变量本身就是一个绝大多数值都为0的不平衡目标变量,这少数的几个样本的Target全部为0并不是什么非常不可思议的事情,因此这个信息可能并没有看上去那么重要。
对于ps_reg_03和ps_car_14,缺失值的存在与否也会影响target=0的所占比例,不过差距就显然没有其他两个特征那么大了,而这两个特征才是缺失比例比较大的。
3.4 缺失值处理
在前述分析中,我们充分研究了缺失值的存在对于Target变量的影响,获得的信息相当重要:对绝大多数的特征而言,“存在缺失值”这件事情本身就有可能会影响Target变量,因此,简简单单地对其进行插补可能并不可取。
对于多分类变量特征的缺失值,这里选择将缺失值插补为-1,也就是把特征的缺失值视为对应特征的一个全新类别,和其他的所属类别一起参与建模。
此外,还有4个并非分类变量的特征存在缺失值,其中,ps_car_11和ps_car_12缺失的部分极少,加在一起也只有6个缺失值而已,对这两个特征只需要插补,不需要保留缺失信息。而另外两个特征ps_reg_03和ps_car_14都是缺失值数量较高的特征,为了保留缺失信息,分别建立两个对应的二分类特征:ps_reg_03_miss和ps_car_14_miss以记录这两个特征的缺失信息,这两个特征会在对应特征出现缺失值的时候取1,否则取0。
此外,由于这几个变量的分布都不对称,因此比起均值,插补中位数更有利于维持原始分布,选择插补中位数。
代码如下:
###缺失值处理:
#对于分类特征,把缺失值视为一个新的分类,插补为-1
miss_cat = [x for x in col_missing if x in catcol]
train[miss_cat] = train[miss_cat].replace(np.nan,-1)
#对于连续特征:
miss_nocat = [x for x in col_missing if x not in miss_cat]
train['ps_reg_03_miss'] = np.zeros(len_train)
train['ps_reg_03_miss'] [train.ps_reg_03.isnull()] = 1
test['ps_reg_03_miss'] = np.zeros(len_test)
test['ps_reg_03_miss'] [test.ps_reg_03.isnull()] = 1
train['ps_car_14_miss'] = np.zeros(len_train)
train['ps_car_14_miss'] [train.ps_car_14.isnull()] = 1
test['ps_car_14_miss'] = np.zeros(len_test)
test['ps_car_14_miss'] [test.ps_car_14.isnull()] = 1
train[miss_nocat] = train[miss_nocat].replace(np.nan,train[miss_nocat].median())
到此,对数据的探索性分析已经告一段落,我们完成了数据清洗工作与质量检查,下一步的工作将会是在这些信息的基础上进行特征工程,获得用于最终建模的特征数据集。在此之前,把清洗完成的数据保存下来:
##保存数据:
train.to_csv('D:\\CZM\\Kaggle\\FinalWork\\train_after_EDA.csv', float_format='%.6f', index=False)
test.to_csv('D:\\CZM\\Kaggle\\FinalWork\\test_after_EDA.csv', float_format='%.6f', index=False)