线段树-基础，典型例题的完整代码

线段树的应用方法总结
http://www.cnblogs.com/rainydays/p/3671220.html

线段树代码，各类线段树的acm题目学习
http://www.cnblogs.com/Mu-Tou/archive/2011/08/11/2134427.html

---

HDU 1166 敌兵布阵

题目地址
http://acm.hdu.edu.cn/showproblem.php?pid=1166

例子图

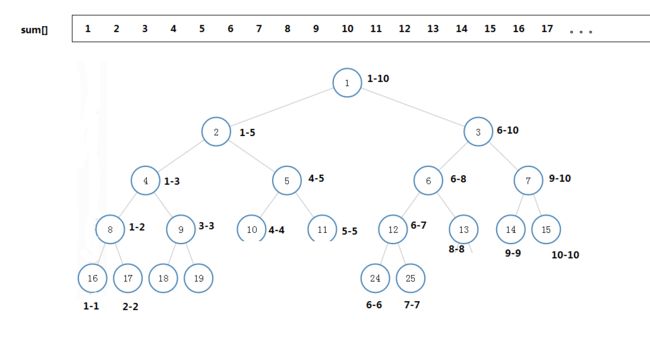
sum[]数组大小是原来大小的4倍
类似堆，数组下标的左右孩子是 i*2 ,i*2 +1(i从1开始)
如上

• sum[1] 存储了 1-10区间的和
• sum[2] 存储了区间[1-5]区间的和
• sum[16] 存储区间[1-1]区间的和，也就是原数组第一个值

ac代码

#include 
#include 


const int N = 50005;

int sum[N * 4];

void PushUP(int rt) {
    sum[rt] = sum[2*rt] + sum[2*rt+1]; // 根 等于左孩子值加上右孩子值
}

void build(int rt, int left, int right) {
    if (left == right) {
        scanf("%d", &sum[rt]);
        return;
    }
    int mid = (right - left) / 2 + left;
    build(2*rt, left, mid);
    build( 2*rt + 1, mid + 1, right);
    PushUP(rt);
}

int query(int qL, int qR, int rt, int left, int right)
{
    if (qL <= left && qR >= right) //查询区间比拥有的区间长，返回根节点
        return sum[rt];

    int ans = 0;
    int mid = (right - left) / 2 + left;
    if (qL <= mid)
        ans += query(qL, qR, rt * 2, left, mid); //可能 与左区间有交集
    if (qR > mid)
        ans += query(qL, qR, rt * 2 + 1, mid + 1, right); //可能 与右区间有交集
    return ans;
}

// 更新left-right中的某个点，需要递归更新这棵树
void update(int pos, int num, int rt, int left, int right)
{
    if (left == right) // 此时有 left == right ==  pos
    {
        sum[rt] += num;
        return;
    }
    int mid = (right - left) / 2 + left;
    if (pos <= mid)
        update(pos, num, rt * 2, left, mid);
    else
        update(pos, num, rt * 2 + 1, mid + 1, right);
    PushUP(rt); // 这里注意要新节点的值
}

int main()
{
    //freopen("in.txt", "r", stdin);
    int T, n;
    scanf("%d", &T);
    for (int cas = 1; cas <= T; cas++) {
        printf("Case %d:\n", cas);
        scanf("%d", &n);
        build(1, 1, n);
        char op[10];
        while (scanf("%s", op)) 
        {
            if (op[0] == 'E') 
                break;
            int a, b;
            scanf("%d%d", &a, &b);
            if (op[0] == 'Q') 
                printf("%d\n", query(a, b, 1, 1 ,n));
            else if (op[0] == 'S')
                update(a, -b, 1, 1, n);
            else 
                update(a, b, 1, 1, n);
        }
    }
        return 0;
}

2016 华为编程题

题目描述

老师想知道从某某同学当中，分数最高的是多少，现在请你编程模拟老师的询问。当然，老师有时候需要更新某位同学的成绩.

输入描述:
输入包括多组测试数据。
每组输入第一行是两个正整数N和M（0 < N <= 30000,0 < M < 5000）,分别代表学生的数目和操作的数目。
学生ID编号从1编到N。
第二行包含N个整数，代表这N个学生的初始成绩，其中第i个数代表ID为i的学生的成绩
接下来又M行，每一行有一个字符C（只取‘Q’或‘U’），和两个正整数A,B,当C为’Q’的时候, 表示这是一条询问操作，他询问ID从A到B（包括A,B）的学生当中，成绩最高的是多少
当C为‘U’的时候，表示这是一条更新操作，要求把ID为A的学生的成绩更改为B。

输出描述:
对于每一次询问操作，在一行里面输出最高成绩.

输入例子:

5 7
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 4 5
U 2 9
Q 1 5

输出例子:

5
6
5
9

https://www.nowcoder.com/practice/3897c2bcc87943ed98d8e0b9e18c4666?tpId=49&tqId=29275&tPage=1&rp=1&ru=/ta/2016test&qru=/ta/2016test/question-ranking

线段树ac

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include  
#include 
#include  
#include  

using namespace std;

const int INF = 0x7fffffff; // 2 147 483 647
const int MIN_INF = - INF - 1; // -2 147 483 648

const int N = 30005;

int n;
int m;

int init[N];
int maxs[N*4];

void PushUP(int rt) {
    maxs[rt] = max(maxs[2*rt], maxs[2*rt+1]);
}

void build(int rt, int left, int right) {
    if (left == right) {
        maxs[rt] = init[left]; //这里赋值注意                        
        return;
    }
    int mid = (right - left) / 2 + left;
    build(2*rt, left, mid);
    build( 2*rt + 1, mid + 1, right);
    PushUP(rt);
}

int query(int qL, int qR, int rt, int left, int right)
{
    if (qL <= left && qR >= right) //查询区间比拥有的区间长，返回根节点
        return maxs[rt];

    int ans = 0;
    int mid = (right - left) / 2 + left;
    if (qL <= mid)
        ans = max(ans, query(qL, qR, rt * 2, left, mid)); //可能 与左区间有交集
    if (qR > mid)
        ans = max(ans, query(qL, qR, rt * 2 + 1, mid + 1, right)); //可能 与右区间有交集
    return ans;
}

// 更新left-right中的某个点，需要递归更新这棵树
void update(int id, int num, int rt, int left, int right)
{
    if (left == right) // 此时有 left == right ==  id
    {
        maxs[rt] = num;
        return;
    }
    int mid = (right - left) / 2 + left;
    if (id <= mid)
        update(id, num, rt * 2, left, mid);
    else
        update(id, num, rt * 2 + 1, mid + 1, right);
    PushUP(rt); // 这里注意要新节点的值
}

int main()
{
    int i;
    while(scanf("%d%d", &n, &m) != EOF)
    {
        for(i=1;i<=n;i++)
        {
            scanf("%d", &init[i]);
        }
        build(1, 1, n);

        for(i=0;ichar c;
            int a;
            int b;
            getchar();
            scanf("%c %d %d", &c, &a, &b);

            if(c == 'Q')
            {
                if(a > b){
                    int tmp = a;
                    a = b;
                    b = tmp;
                }
                int val = query(a, b, 1, 1, n);
                printf("%d\n", val);
            }else{
                update(a, b, 1, 1, n);
            }
        }
    }
    return 0;
}