解析MATLAB中的extendedKalmanFilter函数
ExtendedKalmanFilter函数
obj = extendedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState,Name,Value)
1.输入参数
- StateTransitionFcn:状态方程。形式取决于您在对象中设置的HasAdditiveProcessNoise属性指定噪声为加性还是非加性:
HasAdditiveProcessNoise为true ——过程噪声w是累加的,并且状态转换函数指定状态如何在上一个时间步随状态值变化:x(k) = f(x(k-1),Us1,…,Usn)
HasAdditiveProcessNoise为false ——过程噪声是非加性的,并且状态转换函数还指定状态如何根据过程噪声进行演化:x(k) = f(x(k-1),w(k-1),Us1,…,Usn) - MeasurementFcn:观测方程。形式取决于您在对象中设置的HasAdditiveMeasurementNoise属性指定噪声为加性还是非加性:
HasAdditiveMeasurementNoise为true ——测量噪声v为加性,并且测量函数指定测量如何根据状态值演变:y(k) = h(x(k),Um1,…,Umn)
HasAdditiveMeasurementNoise为false —测量噪声为非加性的,并且测量函数还指定输出测量如何随测量噪声而变化:y(k) = h(x(k),v(k),Um1,…,Umn) - InitialState:状态初值。初始状态估计值,指定为M维向量,其中M是系统中的状态数。指定的值存储在对象的State属性中,如果将InitialState指定为列向量,则State也是列向量,predict和correct命令将状态估计值作为列向量返回。否则,返回行向量。
2.属性
- HasAdditiveMeasurementNoise:测量噪声特性,指定为以下值之一:
true——测量噪声v是累加的。 在MeasurementFcn中指定的测量函数h具有以下形式:y(k) = h(x(k),Um1,…,Umn)
false——测量噪声是非加性的。 测量功能指定输出测量如何根据状态和测量噪声而变化:y(k) = h(x(k),v(k),Um1,…,Umn)
HasAdditiveMeasurementNoise是不可调整的属性,您只能在对象构造期间指定它,您不能使用点表示法更改它。 - HasAdditiveProcessNoise:过程噪声特性,指定为以下值之一:
true——过程噪声w是累加的。 StateTransitionFcn中指定的状态转换函数f具有以下形式:x(k) = f(x(k-1),Us1,…,Usn)
false——过程噪声是非累加的。 状态转换函数指定状态如何根据状态变化并在上一个时间步处理噪声:x(k) = f(x(k-1),w(k-1),Us1,…,Usn)
HasAdditiveProcessNoise是不可调整的属性,您只能在对象构造期间指定它,您不能使用点表示法更改它。 - MeasurementFc:观测方程。
- MeasurementJacobianFcn:观测方程的雅克比函数。MeasurementJacobianFcn是不可调整的属性。您可以在对象构造过程中使用correct命令之前或在对象构造之后使用点标记来指定一次。使用correct命令后,您将无法更改它。
- MeasurementNoise:测量噪声协方差矩阵。MeasurementNoise是可调属,您可以使用点表示法更改它
- ProcessNoise:过程噪声协方差矩阵。ProcessNoise是可调属,您可以使用点表示法更改它
- State:状态值。初始值是您在对象创建期间在InitialState输入参数中指定的值,State是可调属,您可以使用点表示法更改它
- StateCovariance:状态估计误差协方差矩阵,指定为标量或M×M矩阵,其中M是系统的状态数。 如果指定标量,系统将自动创建一个M×M对角矩阵。当您对在InitialState输入参数中指定的初始状态值没有信心时,请为协方差指定一个较高的值。StateCovariance是可调属性,您可以在使用正确或预测命令后使用点表示法更改它。
- StateTransitionFcn:状态方程
- StateTransitionJacobianFcn:状态方程的雅克比函数。StateTransitionJacobianFcn是不可调整的属性。您可以在对象构造过程中使用correct命令之前或在对象构造之后使用点标记来指定一次。使用correct命令后,您将无法更改它。
3.输出参数
用于在线状态估计的扩展卡尔曼过滤器对象,作为extendedKalmanFilter对象返回。 使用指定的属性创建此对象。 使用correct和predict命令来估计状态,并使用扩展的卡尔曼滤波算法来估计状态估计误差的协方差。
当您使用predict时,obj.State和obj.StateCovariance将使用k–1时刻的状态值更新k时刻的预测值。使用correct时,使用k时刻的测量数据,进行对k的估计,同时更新obj.State和obj.StateCovariance。
实例
对前一篇文章中的例题进行滤波:
clc;
clear;
T=0.05;
T_go=10;
t=0:T:T_go-T;
N=T_go/T;
Q=[0.01,0;0,0.0001];
R=[0.1,0;0,0.1];
%模拟测量值
x=zeros(2,N);
x(:,1)=[1;0];
z=zeros(2,N);
mu=[0;0];
w=mvnrnd(mu,Q,N)';
v=mvnrnd(mu,R,N)';
for k=1:N-1
x1=x(1,k);x2=x(2,k);
w1=w(1,k);w2=w(2,k);
x(:,k+1)=[x1+T*x2+w1;-10*T*sin(x1)+(1-T)*x2+w2];
x1=x(1,k+1);x2=x(2,k+1);
v1=v(1,k+1);v2=v(2,k+1);
z(:,k+1)=[2*sin(x1/2)+v1;x1/2+v2];
end
%EKF
xk=zeros(2,N);
xk(:,1)=[1;0];
obj=extendedKalmanFilter(@StateFcn,@MeasurementFcn,xk(:,1),...
'ProcessNoise',Q,...
'MeasurementNoise',R,...
'StateTransitionJacobianFcn',@StateJacobianFcn,...
'MeasurementJacobianFcn',@MeasurementJacobianFcn);
for k=1:N-1
[PredictedState,PredictedStateCovariance] = predict(obj);
[CorrectedState,CorrectedStateCovariance] = correct(obj,z(:,k));
xk(:,k+1)=CorrectedState;
end
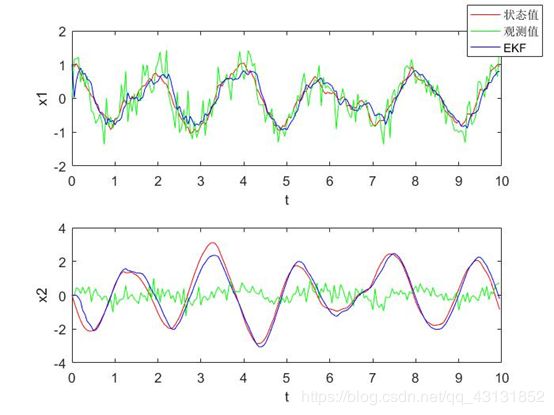
subplot(2,1,1)
plot(t,x(1,:),'-r',t,z(1,:),'-g',t,xk(1,:),'-b');
xlabel('t')
ylabel('x1')
subplot(2,1,2)
plot(t,x(2,:),'-r',t,z(2,:),'-g',t,xk(2,:),'-b');
xlabel('t')
ylabel('x2')
legend('状态值','观测值','EKF');
function [ x ] = StateFcn( x )
T=0.05;
x=[x(1)+T*x(2);-10*T*sin(x(1))+(1-T)*x(2)];
end
function [ z ] = MeasurementFcn( x )
z=[2*sin(x(1)/2);x(1)/2];
end
function [ dfdx ] = StateJacobianFcn( x)
T=0.05;
dfdx=[1,T;-10*T*cos(x(1)),1-T];
end
function [ dhdx ] = MeasurementJacobianFcn( x )
dhdx=[cos(x(1)/2),0;1/2,0];
end