2019年6月20日最短路算法讲义
算法大纲
Q群是Acwing算法交流群2:728297306.
因为四大最短路算法大家应该都明白,所以我们就不讲了,然后根据群友们提出的建议,我们今天讲一讲SPFA求负环,以及最短路和其他算法的配合,等方面的知识.
SPFA求负环
我们先来具体分析一下SPFA算法.
对于SPFA而言,我们发现它是具有几点特殊性质的.
第一步,从SPFA的核心点来分析.
\[ (x,y,z)表示为(x,y)这条有向边的权值为z \\ dist[x]表示从1号节点到x号节点的最短路径 \]
如果说我们发现图中出现如下这张图,那么我们就称之为三角不等式.
我们现在要从\(1\)号节点走到\(3\)号节点,然后我们发现了有这个不等式出现,那么就是三角不等式.
刚开始的话,我们的
\[ dist[3]=dist[1]+ver[1][3] \]
但是当我们的\(2\)号节点出现后,就不一样了.
\[ dist[3] \ge dist[2]+ver[2][3] \]
然后我们就不等不更新我们的\(dist[3]\).所以就会出现如下操作
\[ dist[3]=dist[2]+ver[2][3] \]
然后此时的话,我们就会发现,目前的\(dist[3]\)是满足三角不等式了.
综上所述三角不等式就是说
\[ 对于每一个点x而言,都必须满足dist[x] \le dist[y]+z,也就是说三角形的第三边,一定小于其他两边之和. \]
然后对于每一次不满足三角不等式的情况,也即是上图这种情况,我们都不得不更新\(dist[3]\)的值.
因此最短路上每一个节点,都得满足我们的三角不等式,否则的话,我们总可以,走一遍上图1->2->3来更新我们的最短路.
上面是我们的三角不等式解说,那么现在我们的核心问题点是如何求负环.
我们发现,如果说一张图上出现了负环,那么我们一定无法满足三角不等式.
我们发现如果图中出现了负环,那么肯定我们的如果来到一个负环上的点,那么肯定是要经过这个负环所有的节点的.
什么是环?环就是这个点往其他点走了若干个节点后,还可以回到这个节点.
既然这么说的话,我们每走一次负环就可以让我们的权值减少一部分,那么既然如此的话,我们既然要走最短路,那么为什么不一直沿着这条最短路走呢?
所以说我们一定会不停地沿着这个负环走一遍又一遍,三角形不等式性质根本就无法满足,既然如此的话,我们就可以通过这个办法去找到负环.
我们知道下面这个性质.
\[ 从1号节点走到n号节点,那么途中肯定最多只会途经n个节点,n-1条边 \]
既然有了这个性质,再加上如果有负环的话,那么我们会不停地经过负环上的每一条边,那么我们为什么不可以开一个数组记录一下呢.
\[ 设cnt[i]表示从1号节点到i号节点,途径cnt[i]条边.那么显然cnt[i] \ge n的话,就会出现负环 \]
因此只有出现负环才会不停地访问负环上的边,普通的环是不会不停地访问的.
不过其实,我们还有一种判断方法.
如果我们发现
\[ 一个点入队次数超过了n,那么肯定也是负环出现了. \]
这是什么意思呢?
和上面的意思其实一样,假如说没有负环,那么一个点肯定不会被访问n次,毕竟
题目选讲
第一题
NOIP2017 Day1 T3
题目描述
策策同学特别喜欢逛公园。公园可以看成一张\(N\)个点\(M\)条边构成的有向图,且没有 自环和重边。其中1号点是公园的入口,\(N\)号点是公园的出口,每条边有一个非负权值, 代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从1号点进去,从\(N\)号点出来。
策策喜欢新鲜的事物,它不希望有两天逛公园的路线完全一样,同时策策还是一个 特别热爱学习的好孩子,它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到\(N\)号点的最短路长为\(d\),那么策策只会喜欢长度不超过\(d + K\)的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮它吗?
为避免输出过大,答案对\(P\)取模。
如果有无穷多条合法的路线,请输出\(-1\)。
输入输出格式
输入格式:
第一行包含一个整数 \(T\), 代表数据组数。
接下来\(T\)组数据,对于每组数据: 第一行包含四个整数 \(N,M,K,P\),每两个整数之间用一个空格隔开。
接下来\(M\)行,每行三个整数\(a_i,b_i,c_i\),代表编号为\(a_i,b_i\)的点之间有一条权值为 \(c_i\)的有向边,每两个整数之间用一个空格隔开。
输出格式:
输出文件包含 \(T\) 行,每行一个整数代表答案。
输入输出样例
输入样例#1:
2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0输出样例#1:
3
-1说明
样例解释1
对于第一组数据,最短路为 \(3\)。 \(1 – 5, 1 – 2 – 4 – 5, 1 – 2 – 3 – 5\) 为 \(3\) 条合法路径。
测试数据与约定
对于不同的测试点,我们约定各种参数的规模不会超过如下
| 测试点编号 | \(T\) | \(N\) | \(M\) | \(K\) | 是否有0边 |
|---|---|---|---|---|---|
| 1 | 5 | 5 | 10 | 0 | 否 |
| 2 | 5 | 1000 | 2000 | 0 | 否 |
| 3 | 5 | 1000 | 2000 | 50 | 否 |
| 4 | 5 | 1000 | 2000 | 50 | 否 |
| 5 | 5 | 1000 | 2000 | 50 | 否 |
| 6 | 5 | 1000 | 2000 | 50 | 是 |
| 7 | 5 | 100000 | 200000 | 0 | 否 |
| 8 | 3 | 100000 | 200000 | 50 | 否 |
| 9 | 3 | 100000 | 200000 | 50 | 是 |
| 10 | 3 | 100000 | 200000 | 50 | 是 |
对于 100%的数据, \(1 \le P \le 10^9,1 \le a_i,b_i \le N ,0 \le c_i \le 1000\)。
数据保证:至少存在一条合法的路线。
解题报告
题意理解
这道题目题意就是让你,统计一下长度为\([d,d+k]\)这个区间内从\(1->n\)的路径总数.
30pts
暴力统计
我们发现这道题目有三个点,也即是数据点1,2,7这三个点都是只需要我们找最短路的路径个数.
既然如此的话,我们不妨在最短路算法中,再开一个额外的数组统计路径个数,去拿到这三十分.
1.如果发现松弛操作的两种路径相等,也就是a->c=a->b+b->c,那么我们就将搜索到的点的路径数加上当前点的路径数,即:
if(dis[i]==dis[k]+ver[k][i])
cnt[i]+=cnt[k];2.如果我们更新了搜索到的点到起点的最短距离,也就是a->c < a->b+b->c ,那么我们将到达改点的路径数改为当前点的路径数,也就是
if(dis[i]>dis[k]+ver[k][i]){
dis[i]=dis[k]+ver[k][i];
cnt[i]=cnt[k];
}70pts
暴力思想
我们其实可以惊奇地发现,就是我们的\(k \le 50\),这说明什么就是我们完全可以暴力地去统计,长度为\(d,d+1,d+2,d+3,...,d+K\)的所有路径.
综上所述我们可以通过搜索算法,去一步步暴力地搜索,找到符合条件的路径.
但是我们发现这个搜索显然复杂度太高了.
各大剪枝
我们对于当前这一步而言,如果说它花费了\(w\)点代价,然后接下来我们统统都以最优秀的最短路走到终点,花费\(s\)点费用.
然后我们惊奇地发现\(w+s>d+k\),那么显然这一步是不合法的,因为它的最小花费代价都大于了我们的最大上限路径长度.
综上所述,第一个剪枝,就是我们的可行性剪枝.
但是我们如何统计一个点到终点的距离呢?难道我们要每一次都跑一遍最短路算法统计吗
其实我们可以通过建立一个反向图,来达到目的地.
- 什么是反向图?
我们以样例为例子.
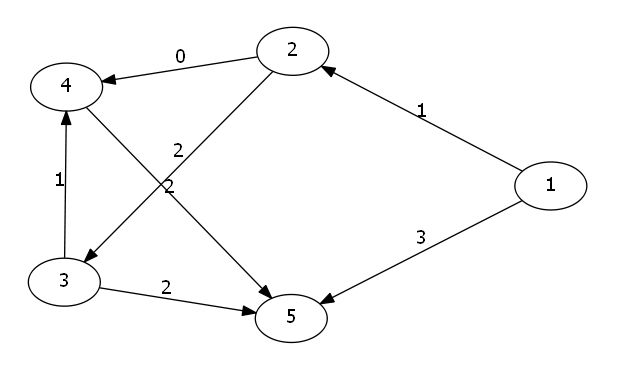
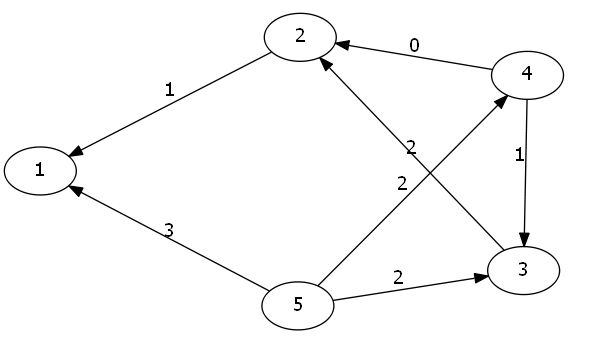
这张图叫做原图.
这张图就是我们的反向图.
所谓的反向图就是将方向统统反过来,原来是a->b,现在改成b->a
- 反向图有什么用处
我们发现反向图最大的用处,就是统计一个点到终点的距离.
因为此时我们的起点是原来的终点N,而现在的终点变成了原来的起点1.所以我们最短路过后,每一个\(dis[i]\)表示为节点\(N\)到\(i\)的距离.
综上所述,我们就这么巧妙地处理了第一个可行性剪枝.
但是我们现在依旧发现了一个问题,我们的时间复杂度还是太高了,所以我们不得不进行记忆化剪枝,也就是利用了了动态规划的思想.
首先我们观察一下,路径长度为\(d+1,d+2,d+3,d+4,...,d+K\)的路径,他们具有以下特征.
对于长度为\(d+1\)的路径而言,我们可以认为它是最短路情况下,多走了一点冤枉路.
对于长度为\(d+2\)的路径而言,我们可以认为它是最短路情况下,多走了二点冤枉路.
对于长度为\(d+3\)的路径而言,我们可以认为它是最短路情况下,多走了三点冤枉路.
将以上路径转化后,我们发现完全可以通过动态规划的思想去处理本问题.
我们设\(f[i][j]\)表示为,当前到达了点\(i\),已经多走了冤枉路\(j\).
那么我们发现状态转移方程也迎刃而解了.
\[ f[u][w]=∑f[v][w+dis[u]−(dis[v]+ver[u][v])] \\ 0 \le w \le K \\ (u,v)为一条边 \\ ver[u][v]表示u到v的距离.\\ w表示当前走了w点冤枉路 \]
我们解释一下上面的状态转移方程的核心点.
\[ w+dis[u]-(dis[v]+ver[u][v]); \]
对于下面这个式子而言,它表示为从起点走到\(v\)所需要花费的最少长度.
\[ dis[v] \]
那么我们的一条最短路径,且是从\(u\)走到\(v\)所花费长度为.
\[ dis[v]+ver[u][v] \]
然后我们的从起点走到\(u\)所花费的最短长度显然为.
\[ dis[u] \]
既然如此那么我们从起点走到\(v**\)的最短路径,减去,我们从起点走到\(u\)然后再走到\(v\)的最短路径,就是我们的多走冤枉路.**
\[ dis[u]-(dis[v]+ver[u][v]); \]
综上所述,这就是我们的思路,那么最后的答案,显然就是.
\[ Ans=\sum_{i=0}^{K}{f[n][i]} \]
100pts
经历了千辛万苦的你,发现如果按照楼上的思路写代码的话,你发现居然只有70pts.
那是因为你忽略掉了-1这种无解的情况.
而-1这个点,其实就是题目中出现了长度为0的一个环 简称0环.
如何判断呢?
- 拓扑排序判断
- Tarjan算法判断
- 搜索的过程中,如果一个点两次进入我们的最短路,那么显然就是0环.
显然这道题目我们使用第三个算法判断.
代码解释
#include
using namespace std;
const int N=1e5+5;//数据范围
const int inf=1e9;//最大值
int t,n,m,k,p,ans,flag,vis[N],dis[N],dp[N][55],vis_dp[N][55],x,y,z;//变量
struct node//最近get到的结构体内置,好好玩啊.模板标记
{
int cnt,edge[N<<1],ver[N<<1],Next[N<<1],head[N];//记得边要乘以2,因为要建立反向图
void init()//初始化
{
cnt=0;
memset(head,0,sizeof(head));
}
void add_edge(int x,int y,int z)//建图
{
edge[++cnt]=y;
ver[cnt]=z;
Next[cnt]=head[x];
head[x]=cnt;
}
void spfa(int s)//SPFA,NOIP是不会卡掉我们的.
{
int i,x;
queueq;
for(i=1; i<=n; i++)
{
vis[i]=0;
dis[i]=inf;
}
q.push(s),vis[s]=1,dis[s]=0;
while(q.size())
{
x=q.front();
q.pop();
vis[x]=0;//出来了
for(i=head[x]; i; i=Next[i])//遍历所有的出边
{
int y=edge[i],z=ver[i];
if(dis[x]+z=0)//如果是在指定偏差区间内的
{
if(vis_dp[y][z])//之前已经进入过最短路径了,那么显然是无解了.
flag=0;
dp[x][k]+=dfs(y,z);//统计
dp[x][k]%=p;//取得取模
}
}
vis_dp[x][k]=0;//已经从最短路径中出来了.
return dp[x][k];//该返回了
}
int main()
{
scanf("%d",&t);
while(t--)
{
clear();
scanf("%d%d%d%d",&n,&m,&k,&p);
for(int i=1; i<=m; i++)
{
scanf("%d%d%d",&x,&y,&z);
g1.add_edge(x,y,z);
g2.add_edge(y,x,z);//不是无向边,是建立反向图
}
g1.spfa(1);
dp[1][0]=1;
for(int i=0; i<=k; i++)
{
ans+=dfs(n,i);//每一个有冤枉路的路径都要加入
ans%=p;//取模快乐
}
dfs(n,k+1);//再来一下判断,主要是判断无解.因为长度为0~k时候走的路,如果和长度为k+1走的路一样,那么显然是无解
if(!flag)//无解了
puts("-1");
else
printf("%lld\n",ans);
}
return 0;
}