滤波估计理论（四）——无迹卡尔曼滤波（Unscented Kalman Filter）

在EKF中我们使用泰勒级数近似非线性函数是为了利用Gaussian的线性性质进行期望（均值）和方差的传递，但在线性化过程中，由于线性化点的选择和高阶项的舍弃，将不可避免的存在线性化误差。如果我们能找到一种方法直接获得非线性变换之后的期望和方差，就可以避免由线性化带来的算法误差，而无迹变换（Unscented Transform，UT）正是这样一种方法。

无迹变换（Unscented Transform）

无迹变换的基本思路是通过确定性地选取一定数量的Sigma点，这些Sigma点的分布和原分布式一致的（即期望和方差相同），采用这一类策略的滤波器通常成为Sigma点Kalman滤波器（Sigma Point Kalman Filter，SPKF）。随后将这些Sigma点逐个按照非线性模型传播，再统计传播之后所有Sigma点的分布以获得非线性变换之后的分布。所以从本质上来说，UT是一种蒙特卡洛估计（Monte Carlo estimation），但其采用策略是确定性，而另一种蒙特卡洛估计方法——粒子滤波（Partical Filter），其采样策略是随机性。

对于Gaussian分布$\mathbf{x}\sim N(\mathbf{\mu },\mathbf{P})$和非线性函数$\mathbf{y}=g(\mathbf{x})$，UT的步骤如下：

1. 按如下规则构建$2n+1$个Sigma点：
   $$\begin{array}{rl}{\mathbf{x}}^{(0)}& =\mathbf{\mu }\\ {\mathbf{x}}^{(i)}& =\mathbf{\mu }+\sqrt{n+\lambda }[\sqrt{\mathbf{P}}{]}_i\\ {\mathbf{x}}^{(i+n)}& =\mathbf{\mu }-\sqrt{n+\lambda }[\sqrt{\mathbf{P}}{]}_i,i=1,2,\cdots ,n\end{array}\text{\hspace{1em}(1)}$$

其中$[\cdot {]}_i$表示矩阵的第$i$列，缩放参数$\lambda$由算法由UT变换参数$\alpha$和$\kappa$决定：
$$\lambda ={\alpha }^2\left(n+\kappa \right)-n\text{\hspace{1em}(2)}$$

2. 将1中构建的$2n+1$个Sigma点按照非线性函数$g$进行传播以获得传播后的Sigma点：
   $$y^{(i)}=g(x^{(i)})\text{\hspace{1em}(3)}$$

3. 统计传播后的Sigma点的均值和方差：
   $$\begin{array}{rl}E\left[g(\mathbf{x})\right]& \simeq {\mathbf{\mu }}_U=\sum _{i=0}^{2n}{w}_i^{(m)}{y}^{(i)}\\ Cov\left[g(\mathbf{x})\right]& \simeq {\mathbf{\Sigma }}_U=\sum _{i=0}^{2n}{w}_i^{(s)}(y^{(i)}-{\mathbf{\mu }}_U)(y^{(i)}-{\mathbf{\mu }}_U{)}^T\end{array}\text{\hspace{1em}(4)}$$

其中权值$w_i^{(s)}$和$w_i^{(s)}$按照如下方法获取：
$$\begin{array}{rl}{w}_0^{(m)}& =\frac{\lambda }{n+\lambda }\\ w_0^{(s)}& =\frac{\lambda }{n+\lambda }+\left(1-{\alpha }^2+\beta \right)\\ w_i^{(m)}& =\frac{1}{2(n+\lambda )}\\ w_i^{(s)}& =\frac{1}{2(n+\lambda )}\end{array}\text{\hspace{1em}(5)}$$

其中$\beta$亦为UT变换的第三个参数。

可以看出，使用UT不需要对函数$g(\mathbf{x})$进行任何的线性化，直接通过一定数量的例子对传播后的高斯分布进行近似，可有效避免在强线性化条件下一阶线性化过程带来的误差。

UKF原理

在了解UT的原理之后，我们很容易就可写出UKF的变换过程。与EKF的推导一样，根据噪声的特性（加性还是非加性），UKF的形式略有不同，由于加性噪声模型在应用中最为广泛，这里我们首先来看加性噪声的情况。

加性噪声下的UKF算法

加性噪声下的系统状态空间方程为：
$$\{\begin{array}{rl}{\mathbf{x}}_{k+1}& =f({\mathbf{x}}_k)+{\mathbf{w}}_k,{\mathbf{x}}_k\sim \mathcal{N}({\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k),{\mathbf{w}}_k\sim \mathcal{N}(0,{\mathbf{Q}}_k)\\ {\mathbf{y}}_{k+1}& =h({\mathbf{x}}_{k+1})+{\mathbf{v}}_k,{\mathbf{v}}_k\sim \mathcal{N}(0,{\mathbf{R}}_{k+1})\end{array}\text{\hspace{1em}(6)}$$

由于系统的状态传播函数$f(\mathbf{x})$和量测函数$h(\mathbf{x})$均为非线性，我们可以分别对其进行两次UT操作。

• 状态预测过程

1. 构造Sigma点：
   $$\begin{array}{rl}{\mathbf{x}}_k^{(0)}& ={\mathbf{\mu }}_k\\ {\mathbf{x}}_k^{(i)}& ={\mathbf{\mu }}_k+\sqrt{n+\lambda }[\sqrt{{\mathbf{P}}_k}{]}_i\\ {\mathbf{x}}_k^{(i+n)}& ={\mathbf{\mu }}_k-\sqrt{n+\lambda }[\sqrt{{\mathbf{P}}_k}{]}_i,i=1,2,\cdots ,n\end{array}\text{\hspace{1em}(7)}$$

2. 基于状态传播函数递推Sigma点:
   $${\hat{\mathbf{x}}}_{k+1}^{(i)}=f({\mathbf{x}}_k^{(i)}),i=0,1,\cdots ,2n$$

3. 统计传播后Sigma点的均值和方差:
   $$\begin{array}{rl}{\hat{\mathbf{\mu }}}_{k+1}& =\sum _{i=0}^{2n}{w}_i^{(m)}{\hat{\mathbf{x}}}_{k+1}^{(i)}\\ {\hat{\mathbf{\Sigma }}}_{k+1}& =\sum _{i=0}^{2n}{w}_i^{(s)}({\hat{\mathbf{x}}}_{k+1}^{(i)}-{\hat{\mathbf{\mu }}}_{k+1})({\hat{\mathbf{x}}}_{k+1}^{(i)}-{\hat{\mathbf{\mu }}}_{k+1}{)}^T+{\mathbf{Q}}_k\end{array}\text{\hspace{1em}(8)}$$

可以看出，由于加性噪声的影响，在统计变换后的均值和方差时，需要加上对应的均值和噪声项（此处噪声均值为0）。

• 量测更新过程
  UKF的量测更新过程同样需要先进行一个UT操作，将状态预测后的${\hat{\mathbf{x}}}_{k+1}\sim \mathcal{N}\left({\hat{\mathbf{\mu }}}_{k+1},{\hat{\mathbf{\Sigma }}}_{k+1}\right)$通过量测函数$h({\mathbf{x}}_{k+1})$进行递推，最后再计算在给定量测${\mathbf{z}}_{k+1}$下的条件概率:

1. 构造Sigma点：
   $$\begin{array}{rl}{\hat{\mathbf{x}}}_{k+1}^{(0)}& ={\hat{\mathbf{\mu }}}_{k+1}\\ {\hat{\mathbf{x}}}_{k+1}^{(i)}& ={\hat{\mathbf{\mu }}}_{k+1}+\sqrt{n+\lambda }[\sqrt{{\mathbf{P}}_k}{]}_i\\ {\hat{\mathbf{x}}}_{k+1}^{(i+n)}& ={\hat{\mathbf{\mu }}}_{k+1}-\sqrt{n+\lambda }[\sqrt{{\mathbf{P}}_k}{]}_i,i=1,2,\cdots ,n\end{array}\text{\hspace{1em}(9)}$$

2. 基于状态传播函数递推Sigma点:
   $${\overline{\mathbf{x}}}_{k+1}^{(i)}=h({\hat{\mathbf{x}}}_{k+1}^{(i)}),i=0,1,\cdots ,2n$$

3. 统计传播后Sigma点的均值，方差以及互协方差:
   $$\begin{array}{rl}{\overline{\mathbf{\mu }}}_{k+1}& =\sum _{i=0}^{2n}{w}_i^{(m)}{\overline{\mathbf{x}}}_{k+1}^{(i)}\\ {\overline{\mathbf{\Sigma }}}_{k+1}& =\sum _{i=0}^{2n}{w}_i^{(s)}({\overline{\mathbf{x}}}_{k+1}^{(i)}-{\overline{\mathbf{\mu }}}_{k+1})({\overline{\mathbf{x}}}_{k+1}^{(i)}-{\overline{\mathbf{\mu }}}_{k+1}{)}^T+{\mathbf{R}}_{k+1}\\ {\mathbf{C}}_{k+1}& =\sum _{i=0}^{2n}{w}_i^{(s)}({\hat{\mathbf{x}}}_{k+1}^{(i)}-{\hat{\mathbf{\mu }}}_{k+1})({\overline{\mathbf{x}}}_{k+1}^{(i)}-{\overline{\mathbf{\mu }}}_{k+1}{)}^T\end{array}\text{\hspace{1em}(10)}$$

回顾Kalman滤波的推导过程可以发现，式(10)同样相当于给出了如下形式的联合分布：
$$\left[\begin{array}{c}{\mathbf{x}}_{k+1}\\ {\mathbf{z}}_{k+1}\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}{\hat{\mathbf{\mu }}}_{k+1}\\ {\overline{\mathbf{\mu }}}_{k+1}\end{array}\right],\left[\begin{array}{cc}{\hat{\mathbf{\Sigma }}}_{k+1}& {\mathbf{C}}_{k+1}\\ {\mathbf{C}}_{k+1}^T& {\overline{\mathbf{\Sigma }}}_{k+1}\end{array}\right]\right)$$

从联合分布$p({\mathbf{x}}_{k+1},{\mathbf{z}}_{k+1})$中求解条件分布$p({\mathbf{x}}_{k+1}|{\mathbf{z}}_{k+1})$则是我们再熟悉不过的了，利用高斯分布的联合分布->条件分布公式（参见Kalman滤波）有：
$$\begin{array}{rl}{\mathbf{K}}_{k+1}& ={\mathbf{C}}_{k+1}{\overline{\mathbf{\Sigma }}}_{k+1}^{-1}\\ {\hat{\mathbf{\mu }}}_{k+1}& ={\hat{\mathbf{\mu }}}_{k+1}+{\mathbf{K}}_{k+1}\left[{\mathbf{z}}_{k+1}-{\overline{\mathbf{\mu }}}_{k+1}\right]\\ {\hat{\mathbf{\Sigma }}}_{k+1}& ={\hat{\mathbf{\Sigma }}}_{k+1}+{\mathbf{C}}_{k+1}{\overline{\mathbf{\Sigma }}}_{k+1}^{-1}{\mathbf{C}}_{k+1}^T={\mathbf{C}}_{k+1}{\overline{\mathbf{\Sigma }}}_{k+1}^{-1}{\overline{\mathbf{\Sigma }}}_{k+1}{\overline{\mathbf{\Sigma }}}_{k+1}^{-1}{\mathbf{C}}_{k+1}^T\\ & ={\mathbf{K}}_{k+1}{\overline{\mathbf{\Sigma }}}_{k+1}{\mathbf{K}}_{k+1}^T\end{array}\text{\hspace{1em}(11)}$$

非加性噪声下的UKF算法

非加性噪声下的UKF算法相比加性噪声下的UKF更为简单，对于如下的非加性噪声模型：
$$\{\begin{array}{rl}{\mathbf{x}}_{k+1}& =f({\mathbf{x}}_k,{\mathbf{w}}_k),{\mathbf{x}}_k\sim \mathcal{N}({\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k),{\mathbf{w}}_k\sim \mathcal{N}(0,{\mathbf{Q}}_k)\\ {\mathbf{y}}_{k+1}& =h({\mathbf{x}}_{k+1},{\mathbf{v}}_k),{\mathbf{v}}_k\sim \mathcal{N}(0,{\mathbf{R}}_{k+1})\end{array}\text{\hspace{1em}(12)}$$

我们只需要做一个如下式所示简单的变换就可将其转化为无噪声问题，随后按照式(1)~式(5)进行更新即可。
$${\mathbf{x}}_k^{\prime }=\left[\begin{array}{c}\mathbf{x}\\ {\mathbf{w}}_k\end{array}\right],{\mathbf{\Sigma }}_k^{\prime }=\left[\begin{array}{cc}{\mathbf{\Sigma }}_k& \\ & {\mathbf{Q}}_k\end{array}\right]$$

对于量测更新过程，我们同样可以如此简化，这里不再赘述。

UKF例程

这里我们来看一个简单的一维例子，假设我们需要随一个常值进行估计，系统的状态空间方程为：
$$\{\begin{array}{rl}{x}_{t+1}& =x_t+w_t\\ z_{t+1}& =\sqrt{x_{t+1}}+v_{t+1}\end{array}$$

完整的代码参见github主页（Bayesian Filter），代码由一个UKF基类及UKF_1D派生类组成，Sigma Points的生成，状态及量测的传递均在基类实现如下：

• Sigma Point生成

void UKF::generateSigmaPoints(){
    VecXd tmp = VecXd::Zero(x_dim_);

    MatXd S_sqrt;
    // Cholsky分解
     S_sqrt = curSigma_.llt().matrixL();
 	// 生成Sigma Points  
    tmp = curMu_;
    sPointsX_.emplace_back(tmp);
    // 1 ~ n & n+1 ~ 2n
    for(int i = 0; i < x_dim_; i++){
        tmp = curMu_ + sqrt(x_dim_ + lambda_) * S_sqrt.col(i);
        sPointsX_.emplace_back(tmp);
    }

    for(int i = 0; i < x_dim_; i++){
        tmp = curMu_ - sqrt(x_dim_ + lambda_) * S_sqrt.col(i);
        sPointsX_.emplace_back(tmp);
    }
}

• 状态传递

void UKF::oneStepPrediction(){
    if(!flag_initiated_){
        cerr << "Please call init() to initiate filter first !\n";
        return;
    }
    // clear containers
    sPointsX_.clear();
    sPointsY_.clear();
    // generate sigma points
    generateSigmaPoints();
    // propogate sigma points by f(x)
    propagateFcn();
    // compute predicted mean and covariance
    curMu_ = calcMean(sPointsY_);
    // cout << "MU_P: " << curMu_.transpose() << endl;
    curSigma_ = calcCov(sPointsY_) + Q_;
}

• 量测传递

void UKF::oneStepUpdate(VecXd &Z){
    if(!flag_initiated_){
        cerr << "Please call init() to initiate filter first !\n";
        return;
    }
    // clear containers
    sPointsX_.clear();
    sPointsY_.clear();
    // generate sigma points
    generateSigmaPoints();
    // propagate sigma points by h(x)
    updateFcn();
    // compute tmp predicted mean and covariance
    VecXd M_tmp = calcMean(sPointsY_); // mu_k
    MatXd S_tmp = calcCov(sPointsY_) + R_; // S_k
    MatXd C_tmp = calcCrossCov(sPointsX_, sPointsY_); // C_k
    // compute estimation state
    MatXd K = C_tmp * S_tmp.inverse();
    curMu_ += K * (Z - M_tmp);
    curSigma_ -= K * S_tmp * K.transpose();
    // cout << "MU_U: " << curMu_.transpose() << endl;
}

派生类UKF_1D中则主要实现不同的状态传递和量测模型，针对本例，对应的函数如下：

namespace myFilter{

UKF_1D::UKF_1D(double alpha, double beta, double kappa){
    alpha_ = alpha;
    beta_ = beta;
    kappa_ = kappa;
}

void UKF_1D::propagateFcn(){
    VecXd tmp = VecXd::Zero(x_dim_);

    for(auto it : sPointsX_){
        tmp = it;
        sPointsY_.emplace_back(tmp);
    }
}

void UKF_1D::updateFcn(){
    VecXd tmp = VecXd::Zero(x_dim_);
    
    for(auto it: sPointsX_){
        tmp(0) = sqrt(it(0));
        sPointsY_.emplace_back(tmp);
    }
}

}

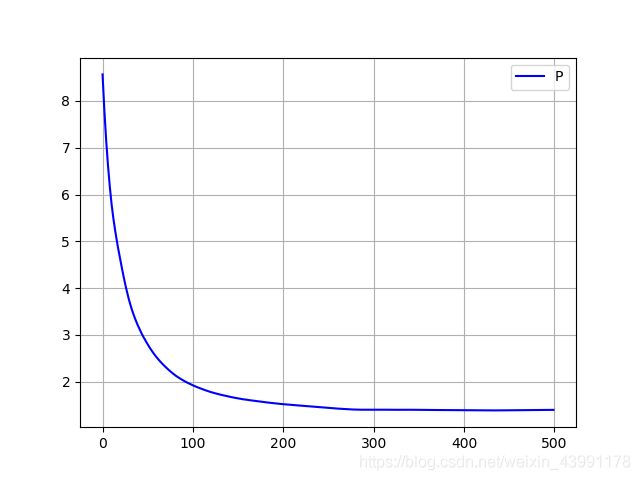
这里我们取$x$的真值为$25$，量测噪声$v_{t+1}\sim \mathcal{N}(0,2.5)$，共进行500次测量，得到的结果如下，其中蓝线为真值，绿线为量测值，红线为UKF的估计值：