PAT甲组1018.Public Bike Management思路与注意点--补充《算法笔记》

A1018

题目链接

个人思路

个人把题目理解错意思了，将从起点到终点的整条路径的自行车数目进行加和，最后得出整条路径总体来看是缺少还是过剩，整条路径的自行车数量是缺少的，出发时就携带；是过剩的，就空手出发。
导致最后答案的首尾两项肯定有一个为0。
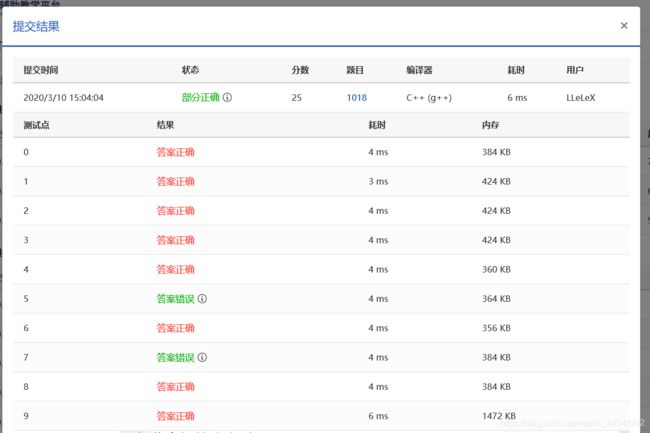
还是题目理解不到位，看到样例就想当然的做，按错误思路居然还通过不少测试点

• 先Dijkstra，完善pre[]集合
• 对pre[]集合dfs

个人思路代码

#include 
using namespace std;
const int maxn = 505;
const int inf = 0x3fffffff;
int Cmax, N, Sp, M;
int curWeight[maxn];//当前顶点自行车个数 
bool vis[maxn];
int G[maxn][maxn];
int d[maxn];
vector<int> pre[maxn];
void Dijkstra()
{
	for(int i = 0; i <= N; ++i)
	{
		int u, udist, mindist = inf;
		for(int j = 0; j <= N; ++j)//寻找最短距离 
		{
			if(!vis[j] && d[j] < mindist)
			{
				u = j;
				udist = mindist = d[j];
			}
		}
		vis[u] = true;
		for(int v = 0; v <= N; ++v)
		{
			if(!vis[v] && G[u][v])
			{
				if(d[u] + G[u][v] < d[v])
				{
					d[v] = d[u] + G[u][v];
					pre[v].clear();
					pre[v].push_back(u);
				}
				else if(d[u] + G[u][v] == d[v])
				{
					pre[v].push_back(u);
				}
			}
		}
	}
}
bool flag;//true:往外带，false:往回拿 
vector<int> optPath, tempPath;
int optSent = inf, optBack = inf;//最佳带出去，最佳带回来 
void dfs(int v)//当前顶点v 
{
	if(v == 0)//边界 
	{
		tempPath.push_back(v);
		
		//计算过程 
		int nodeCnt = tempPath.size() - 1;//除起点外，路径上节点个数 
		int targetNum = (nodeCnt * Cmax) / 2;//目标数量 
		int tempSent = 0, tempBack = 0, curNum = 0;
		for(int i = nodeCnt; i >= 0; i--)
		{
			int id = tempPath[i];
			curNum += curWeight[id];//路径上自行车的总量 
		}
		if(curNum < targetNum)//判断整条路应该往外带 
			tempSent = targetNum - curNum;//往外带的数量
		else//整条路应该往回拿 
			tempBack = curNum - targetNum;//往回拿的数量 
			
		if(tempSent < optSent)//首先选择往外带最少的 
		{
			flag = true;
			optSent = tempSent;
			optPath = tempPath;
			if(tempBack > 0)//说明这条路是往回拿的，tempSent = 0；否则optBack = inf 
				optBack = tempBack;
		} 
		else if(tempSent == optSent)//说明都是0，路径是往回拿的 
		{
			flag = false;
			if(tempBack < optBack)//比较往回拿最少的
			{
				optBack = tempBack;
				optPath = tempPath;
				optSent = tempSent;
			} 
		}
		tempPath.pop_back();
		return;
	}
	tempPath.push_back(v);
	for(int i = 0; i < pre[v].size(); ++i)
	{
		dfs(pre[v][i]);
	}
	tempPath.pop_back();
}
int main(int argc, char *argv[]) {
	scanf("%d%d%d%d", &Cmax, &N, &Sp, &M);
	for(int i = 1; i <= N; ++i)
		scanf("%d", &curWeight[i]);
	for(int i = 0; i < M; ++i)
	{
		int s1, s2, t;
		scanf("%d%d%d", &s1, &s2, &t);
		G[s1][s2] = G[s2][s1] = t;
	}
	//初始化 
	for(int i = 0; i <= N; ++i)//下标从0到N 
	{
		d[i] = inf;
	}
	d[0] = 0;
	Dijkstra();
	dfs(Sp);
	if(optBack == inf)//往外带 
		optBack = 0;
	if(optSent == inf)//往回拿 
		optSent = 0;
	printf("%d ", optSent);
	for(int i = optPath.size() - 1; i >= 0; i--)
	{
		printf("%d", optPath[i]);
		if(i > 0)
			printf("->");
		else
			printf(" ");
	}
	printf("%d", optBack);
	return 0;
}

本题思路

本题找出最短路径后，进行dfs。从起点到终点遍历过程中，对各个站点的自行车数量有序进行填充或拿走的，即第一个点如果不够就补充，如果多了就拿走；随后到第二个点，第二个如果不够就用手里的补充，如果超过就继续拿走……以此类推
值得学习提前将所有权值减去Cmax / 2，运算简化了很多

AC代码

#include 
using namespace std;
const int maxn = 505;
const int inf = 0x3fffffff;
int Cmax, N, Sp, M;
int weight[maxn];//当前顶点自行车个数 
bool vis[maxn];
int G[maxn][maxn];
int d[maxn];
vector<int> pre[maxn];
void Dijkstra()
{
	for(int i = 0; i <= N; ++i)
	{
		int u, udist, mindist = inf;
		for(int j = 0; j <= N; ++j)//寻找最短距离 
		{
			if(!vis[j] && d[j] < mindist)
			{
				u = j;
				udist = mindist = d[j];
			}
		}
		vis[u] = true;
		for(int v = 0; v <= N; ++v)
		{
			if(!vis[v] && G[u][v])
			{
				if(d[u] + G[u][v] < d[v])
				{
					d[v] = d[u] + G[u][v];
					pre[v].clear();
					pre[v].push_back(u);
				}
				else if(d[u] + G[u][v] == d[v])
				{
					pre[v].push_back(u);
				}
			}
		}
	}
}
vector<int> optPath, tempPath;
int optNeed = inf, optRemain = inf;//最佳带出去，最佳带回来 
void dfs(int v)//当前顶点v 
{
	if(v == 0)//边界 
	{
		tempPath.push_back(v);
		
		//计算过程 
		int tempNeed = 0, tempRemain = 0;//当前需要带出去的，当前手上剩余的 
		for(int i = tempPath.size() - 1; i >= 0; i--)
		{
			int id = tempPath[i];
			if(weight[id] > 0)//说明是有多余的 
			{
				tempRemain += weight[id];
			}
			else//说明是不够的 
			{
				int absW = weight[id] * -1;
				if(tempRemain > absW)//手上的足以补足 
				{
					tempRemain += weight[id];
				}
				else//不足以补足，需要从起点带 
				{
					tempNeed += absW - tempRemain;
					tempRemain = 0;
				}
			}
		}
		 
			
		if(tempNeed < optNeed)//首先选择往外带最少的 
		{
			optPath = tempPath;
			optNeed = tempNeed;
			optRemain = tempRemain;
		} 
		else if(tempNeed == optNeed)
		{
			
			if(tempRemain < optRemain)//比较往回拿最少的
			{
				optPath = tempPath;
				optRemain = tempRemain;
			} 
		}
		tempPath.pop_back();
		return;
	}
	tempPath.push_back(v);
	for(int i = 0; i < pre[v].size(); ++i)
	{
		dfs(pre[v][i]);
	}
	tempPath.pop_back();
}
int main(int argc, char *argv[]) {
	scanf("%d%d%d%d", &Cmax, &N, &Sp, &M);
	for(int i = 1; i <= N; ++i)
		scanf("%d", &weight[i]);
	for(int i = 0; i < M; ++i)
	{
		int s1, s2, t;
		scanf("%d%d%d", &s1, &s2, &t);
		G[s1][s2] = G[s2][s1] = t;
	}
	//初始化 
	for(int i = 0; i <= N; ++i)//下标从0到N 
	{
		d[i] = inf;
		if(i > 0)
			weight[i] -= Cmax / 2;//把每个站点的点权都减去Cmax/2 
	}
	d[0] = 0;
	Dijkstra();
	dfs(Sp);
	printf("%d ", optNeed);
	for(int i = optPath.size() - 1; i >= 0; i--)
	{
		printf("%d", optPath[i]);
		if(i > 0)
			printf("->");
		else
			printf(" ");
	}
	printf("%d", optRemain);
	return 0;
}

附赠测试用例

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1
ans
3 0->2->3 0

10 3 3 5
6 7 10
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1
ans
0 0->1->3 6

10 4 4 6
2 7 0 10
0 1 2
0 2 2
1 3 1
2 4 2
0 4 5
3 4 1
ans
0 0->2->4 7

10 4 4 5
4 8 9 0
0 1 1
1 2 1
1 3 2
2 3 1
3 4 1
ans
1 0->1->2->3->4 2