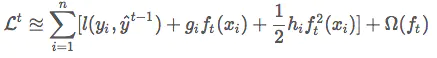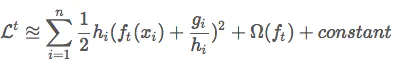高级算法梳理-XGB
XGB算法梳理
1、算法原理
XGBoost(eXtreme Gradient Boosting)算法是Gradient Boosting算法的高效实现版本,因其在应用实践中表现出优良的效果和效率,因而也被工业界广为推崇。
想要了解XGBoost算法的原理,首先需要理解Boosting算法。简单来说,Boosting算法是将个体学习器集成为更复杂学习器的机器学习方法,它更强调个体学习器之间存在强依赖关系,因此也可认为是串行集成学习方法。相比下,Bagging算法则属于并行集成学习方法。
Boosting算法的基本原理是:首先用初始样本训练一个基学习器,根据学习表现对样本分布进行调整,使得表现差的样本获得更多的关注,然后不断迭代用调整分布后的样本训练下一个基学习器,直到基学习器数量达到指定数目。
Boosting算法族中最著名的即是Freund于1997年提出的AdaBoost算法,可将其理解为“加性模型”,即最终的学习器为t个基学习器的“加权和”模型,每次使用训练错误的样本训练新的基学习器,并通过权重调整降低之前表现不佳的学习器的影响,最终降低集成学习器的结果偏差。
2001年,Freund又提出了Gradient Boosting框架,将损失函数扩展到更一般的情况,即通过梯度计算回归拟合的残差(准确应称之为伪残差),基于该残差生成新的基学习器,并计算其最优的叠加权重值。如果选择基分类器为决策树(如CART树),则对应为GBDT算法。
CART树是分类树,并不满足GB回归损失函数的要求,因此需要将分类GINI系数指标替换为最小均方差,即当所有分枝的预测结果唯一或是达到叶节点数量上限时,以该树所有节点的预测均值作为该分类器的预测结果。此外,GBDT还借鉴了Bagging集成学习的一些思想,例如通过随机抽样提高模型的泛化能力,通过交叉验证选择最优参数等。
2014年,陈天奇博士提出了XGBoost算法,它可认为是在GBDT算法基础上的进一步优化。首先,XGBoost算法在基学习器损失函数中引入了正则项,控制减少训练过程当中的过拟合;其次,XGBoost算法不仅使用一阶导数计算伪残差,还计算二阶导数可近似快速剪枝的构建新的基学习器;此外,XGBoost算法还做了很多工程上的优化,例如支持并行计算、提高计算效率、处理稀疏训练数据等等。
综上分析,XGBoost算法源起于Boosting集成学习方法,在演化过程中又融入了Bagging集成学习方法的优势,通过Gradient Boosting框架自定义损失函数提高了算法解决通用问题的能力,同时引入更多可控参数即可针对问题场景进行优化,最后通过工程实现方面细节优化,在保证算法结果稳定的同时还可高效处理大规模数据,可扩展支持不同编程语言。这些因素共同使它成为了工业界的主流机器学习算法之一。
2、损失函数
自定义损失函数(指定grad、hess)
(1)损失函数
![]()
(2)grad、hess推导
![]()
3、分裂结点算法(分位点算法 -- quantile sketch)
GBoost利用泰勒公式将目标函数的作用发挥到极致。
目标函数了树生成,叶子节点分数和叶子节点分裂等等方方面面。
决策树的学习过程就是为了找出最优的决策树,然而从函数空间里所有的决策树中找出最优的决策树是NP-C问题,所以常采用启发式(Heuristic)的方法,如CART里面的优化GINI指数、剪枝、控制树的深度。这些启发式方法的背后往往隐含了一个目标函数,这也是大部分人经常忽视掉的。
XGBoost则采取了一种trade off,近似地找到best split,就是标题的一种weighted quantile sketch算法。 既然样本数量太大,我们可不可以按比例来选择,从n个样本中抽取k个样本来进行计算,取k个样本中的最优值作为split value,这样就大大减少了运算数量。这就是k分位点选取的思想,即quantile sketch。
按权重的分位点算法 -- weighted quantile sketch
(1)来源(为什么)
要如何抽取k个样本?10000个样本取10个的话,每1000个样本计算一次split value看似可行,其实是不可以的,我们要均分的是loss,而不是样本的数量,而每个样本对loss的贡献可能是不一样的,按样本均分会导致loss分布不均匀,取到的分位点会有偏差。
回忆loss function的早期形式:
对其变形得到:
这个形式的loss说明了, xi的loss也可以看做是以−gi/hi作为label的均方误差,乘以大小为hi的权重,换句话说,xi对loss的贡献权重为hi。
那么,对loss取k分位点就是对误差的均分
(2)具体划分策略
那么具体划分策略如何计算?paper提出了一个weighted quantile sketch,即将样本对应的残差二阶导h作为划分依据,将同范围h占比的特征值划分到同一范围内。
![]()
这里讲的占比即排序函数r(z),特征x小于z的样本中二阶导的总和占比,另外s为划分节点。h相当于是一个加权系数weight,不同于权重为1的情况(即每个范围有相同的样本数),残差二阶导差异越大的地方,样本分布越稀疏,反之则稠密。个人理解,其加权的意义在于,把候选节点选取的机会更多地让于二阶导更大的地方,同时忽略导数差异小的节点。
(3)应用
流程如下:
不同于基本的穷举算法,paper指出两种近似算法:一种是全局算法,即在初始化tree的时候划分好候选节点,并且在树的每一层都使用这些候选节点;另一种是局部算法,即每一次划分的时候都重新计算候选节点。这两者各有利弊,全局算法不需要多次计算候选节点,但需要一次获取较多的候选节点供后续树生长使用,而局部算法一次获取的候选节点较少,可以在分支过程中不断改善,即适用于生长更深的树,两者在effect和accuracy做trade off。
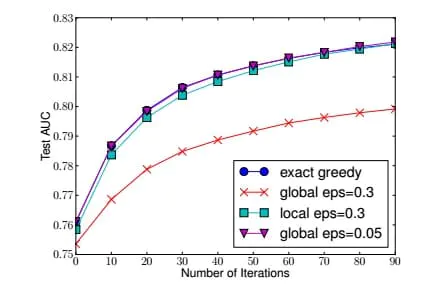
局部算法:这个k分位点的选取是近似的,不能像遍历一样保证取到的split value是最佳的split value。不过经过试验,k取到3的时候,算法性能就已经相差无几了,见下图:
实验中发现,全局k分位点取20和局部k分位点取3,得到了近似的效果。
4、正则化
GBoost在代价函数里加入了正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲,正则项降低了模型的variance,使学习出来的模型更加简单,防止过拟合,这也是xgboost优于传统GBDT的一个特性。
5、对缺失值处理
通常情况下,我们人为在处理缺失值的时候大多会选用中位数、均值或是二者的融合来对数值型特征进行填补,使用出现次数最多的类别来填补缺失的类别特征。
很多的机器学习算法都无法提供缺失值的自动处理,都需要人为地去处理,但是xgboost模型却能够处理缺失值,也就是说模型允许缺失值存在。
原是论文中关于缺失值的处理将其看与稀疏矩阵的处理看作一样。在寻找split point的时候,不会对该特征为missing的样本进行遍历统计,只对该列特征值为non-missing的样本上对应的特征值进行遍历,通过这个技巧来减少了为稀疏离散特征寻找split point的时间开销。在逻辑实现上,为了保证完备性,会分别处理将missing该特征值的样本分配到左叶子结点和右叶子结点的两种情形,计算增益后选择增益大的方向进行分裂即可。可以为缺失值或者指定的值指定分支的默认方向,这能大大提升算法的效率。如果在训练中没有缺失值而在预测中出现缺失,那么会自动将缺失值的划分方向放到右子树。
原文的伪代码如下:
6、优缺点
XGBoost的性能在GBDT上又有一步提升,而其性能也能通过各种比赛管窥一二。坊间对XGBoost最大的认知在于其能够自动地运用CPU的多线程进行并行计算,同时在算法精度上也进行了精度的提高。
由于GBDT在合理的参数设置下,往往要生成一定数量的树才能达到令人满意的准确率,在数据集较复杂时,模型可能需要几千次迭代运算。但是XGBoost利用并行的CPU更好的解决了这个问题。
其实XGBoost和GBDT的差别也较大,这一点也同样体现在其性能表现上,详见XGBoost与GBDT的区别。
---------------------
7、应用场景
GBDT和XGBoost区别
(1)传统的GBDT以CART树作为基学习器,XGBoost还支持线性分类器,这个时候XGBoost相当于L1和L2正则化的逻辑斯蒂回归(分类)或者线性回归(回归);
(2)传统的GBDT在优化的时候只用到一阶导数信息,XGBoost则对代价函数进行了二阶泰勒展开,得到一阶和二阶导数;
(3)XGBoost在代价函数中加入了正则项,用于控制模型的复杂度。从权衡方差偏差来看,它降低了模型的方差,使学习出来的模型更加简单,放置过拟合,这也是XGBoost优于传统GBDT的一个特性;
(4)shrinkage(缩减),相当于学习速率(XGBoost中的eta)。XGBoost在进行完一次迭代时,会将叶子节点的权值乘上该系数,主要是为了削弱每棵树的影响,让后面有更大的学习空间。(GBDT也有学习速率);
(5)列抽样。XGBoost借鉴了随机森林的做法,支持列抽样,不仅防止过 拟合,还能减少计算;
(6)对缺失值的处理。对于特征的值有缺失的样本,XGBoost还可以自动 学习出它的分裂方向;
(7)XGBoost工具支持并行。Boosting不是一种串行的结构吗?怎么并行 的?注意XGBoost的并行不是tree粒度的并行,XGBoost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值)。XGBoost的并行是在特征粒度上的。我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),XGBoost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代 中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
---------------------
8、sklearn参数
xgb使用sklearn接口(推荐)
官方
会改变的函数名是:
eta -> learning_rate
lambda -> reg_lambda
alpha -> reg_alpha
机器学习sklearn参数解释(GDBT+XGBOOST):https://blog.csdn.net/wuxiaosi808/article/details/78036633
本文参考文献及学习资料:
[1] https://zhuanlan.zhihu.com/p/31182879
[2] https://zhuanlan.zhihu.com/p/29940764
[3] https://blog.csdn.net/a819825294/article/details/51206410
[4]官方文档:
http://xgboost.readthedocs.io/en/latest/
[5]Github:
https://github.com/dmlc/xgboost
[6]Xgboost论文:
http://cran.fhcrc.org/web/packages/xgboost/vignettes/xgboost.pdf
[7]陈天奇的boosting tree的ppt:
http://homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
[8]Xgboost调参:
http://blog.csdn.net/wzmsltw/article/details/50994481
[9]GBDT资料:
http://www.jianshu.com/p/005a4e6ac775
[10]XGB之分位点算法:https://www.jianshu.com/p/22b82127644a
[11]XGB对缺失值的处理:https://www.jianshu.com/p/5b8fbbb7e754
[12]xgboost的优点与GBDT对比:https://blog.csdn.net/hfzd24/article/details/76889428
[13]RF、GBDT、XGBoost面试级整理:https://blog.csdn.net/qq_28031525/article/details/70207918