图解 "赫夫曼编码"?(赫夫曼大叔开讲啦！！！）

点击关注上方“五分钟学算法”，

设为“置顶或星标”，第一时间送达干货。

转自景禹

小禹禹，你知道赫夫曼树吗？不知道哎！

那景禹今天就给你细细道来，在介绍赫夫曼树之前，我们一起先来弄清楚和树有关的四个概念。

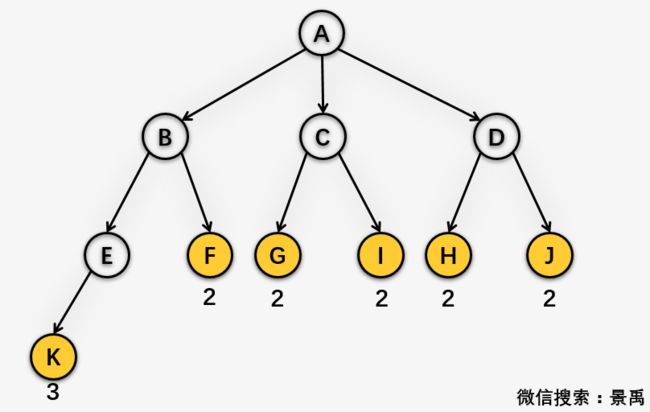
概念一：什么结点的路径长度？

从根结点到该结点的路径上的连接数。

小禹禹：还是不知道

结点K的路径长度就是从根结点A到结点K的路径上的连接数，也就是我们看到红色连边，当然就是3喽！

小禹禹（原来如此）

概念二：什么是树的路径长度呢？

树中每个叶子结点的路径长度之和！

小禹禹：这个简单，就是叶子结点K、F、G、I、H和 J 各自的路径长度加起来呗 ！

很聪明么，就是3+2 * 5=13啦！结点K的路径长度为3，其他5个结点的路径长度都是2。

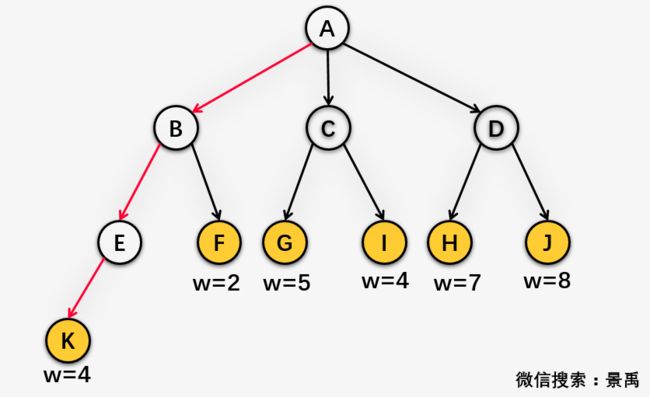
概念三：什么是的结点带权路径长度？

结点的路径长度与结点权值的乘积。

结点K的路径长度为3，权重w=4，所以结点K的带权路径长度为3 * 4 = 12

概念四：什么树的带权路径长度?

WPL(Weighted Path Length)是树中所有叶子结点的带权路径长度之和。

对比树的结点路径长度，树的带权路径长度=3 * 4 + 2 * （2+5+4+7+8）= 64 （哈哈，景禹是不是故意给我整一个这么有意义的数字的）就是啦，准确无疑~~

小禹禹：天呢，一棵树上还有这么多东东！

树：哈哈，因为我厉害呀，你们需要我，我不多给自己增加些分量怎么行？

为了给大家讲清楚赫夫曼树，今天景禹请来了我们麻省理工学院的赫夫曼大叔，景禹先拍一拍赫夫曼大叔的马屁。

在数据膨胀、信息爆炸的今天，数据压缩的意义不言而喻。谈到数据压缩，就不能不提赫夫曼（Huffman）编码，赫夫曼编码是首个实用的压缩编码方案，即使在今天的许多知名压缩算法里，依然可以见到赫夫曼编码的影子。

另外，在数据通信中，用二进制给每个字符进行编码时不得不面对的一个问题是如何使电文总长最短且不产生二义性。根据字符出现频率，利用赫夫曼编码可以构造出一种不等长的二进制，使编码后的电文长度最短，且保证不产生二义性。

下面有请我们的赫夫曼博士本人给你介绍一下自己的成果。

前面景禹给小禹禹介绍了WPL，我就不在此陈述了，需要指出的是：WPL的值越小，说明构造出来的二叉树性能就越优。我当初就死命的涂涂画画，最终研究出了一种最优的构造方法，我也挺辛苦，就以自己名字命名为赫夫曼树，小禹禹先来看一下赫夫曼树的构造过程。

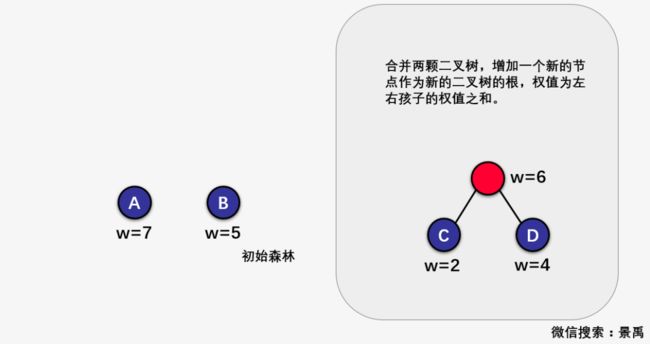
首先我给你们给出一个初始森林，如下图：

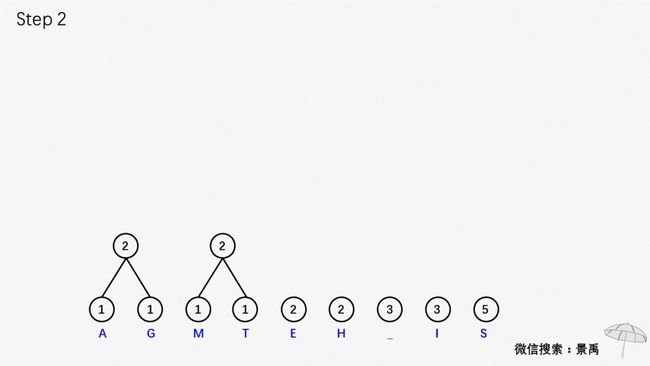
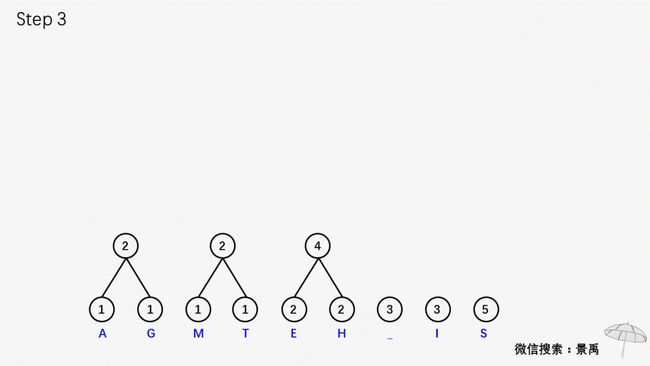
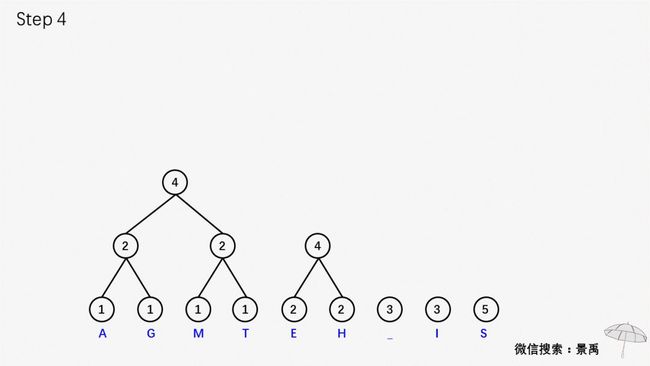
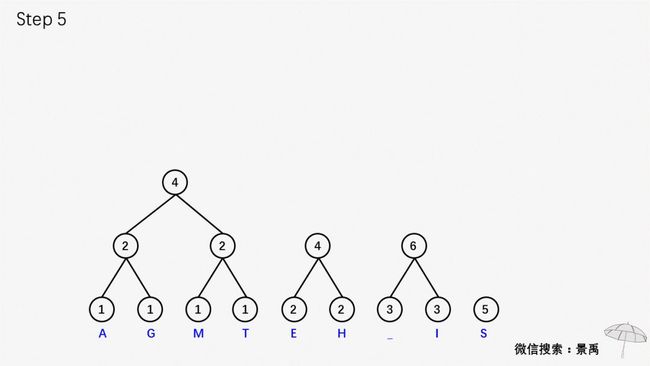
第一步：森林中选择出两颗结点的权值最小的二叉树

第二步：合并两颗二叉树，增加一个新的节点作为新的二叉树的根，权值为左右孩子的权值之和。

接下来就是重复以上两步骤了，我们直接来看一下赫夫曼大叔给大家准备的动画。

定长编码（fixed-length codes）：像ASCII编码（后台回复：ascii 就可以获取ASCII编码表）、Unicode编码。ASCII编码每一个字符使用8个bits，能够编码256个字符；Unicode编码每个字符占16个bit，能够编码65536个字符，包含所有ASCII编码的字符。

定长编码的缺陷：

浪费空间！对于仅包含ASCII字符的纯文本消息，Unicode使用的空间是ASCII的两倍，两种方式都会造成空间浪费；字符“ a”和“ e”的出现频率比“ q”和“ z”的出现频率高，但是他们都占用了相同位数的空间。要解决定长编码的缺陷，便有了下面的变长编码。

变长编码：单个编码的长度不一致，可以根据整体出现频率来调节，出现频率越高，编码长度越短。

变长编码优于定长编码的是，变长编码可以将短编码赋予平均出现频率较高的字符，同一消息的编码长度小于定长编码。

前缀属性：

字符集当中的一个字符编码不是其他字符编码的前缀，则这个字符编码具有前缀属性。所谓前缀，一个编码可以被解码为多个字符，表示不唯一。比如，abcd需要编码表示，设a=0 b=10 c=110 d=11，则表示110可以是c也可以是da。不理解没关系，我老头子给你准备了例子。

小禹禹们，还不理解，我老头也是心累呀，那你再看下面的例子

前缀码：所谓的前缀码，就是没有任何码字是其他码字的前缀

终于解决掉了前缀属性的问题，关于前缀码的定义，我老头子不给你们这些小屁孩读了！不过得考考你们

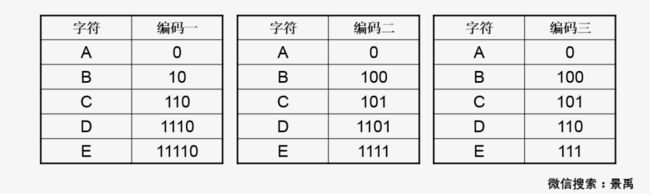
问题：请设计变长的前缀码，使用22位对消息DEAACAAAAABA进行编码

赫夫曼大叔解答：使用22位对消息DEAACAAAAABA进行编码的前缀码编码方案很多。消息中字符 A 出现了8次，字符 B、C、D 和 E 均只出现了1次；字符 A 用一个bit位表示，A=0，其他字符的编码均不能以0开头；B=10、C=110、D=1110和 E=11110；DEAACAAAAABA=1110111100011000000100，刚好22位。老头子再给你们提供其他几种，自己下去尝试尝试。

给你们铺垫了这么多，也该讲讲我老头子自己的东西了！我所提出的赫夫曼编码就是一种前缀码，在进行编码的时候，我是通过一颗赫夫曼编码树（Huffman coding tree）进行的，所以先来看一下我构造的这颗老头子编码树的一些特性呗！

1. 霍夫曼编码树是一颗二叉树

• 每片叶子结点都包含一个字符

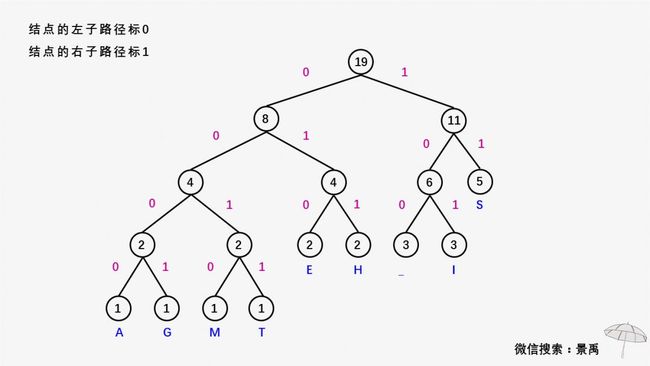
• 从结点到其左孩子的路径上标记0

• 从结点到其右孩子的路径上标记1

1. 从根结点到包含字符的叶子结点的路径上获得叶结点的编码

2. 编码均具有前缀属性

• 每一个叶结点不能出现在到另一个叶结点的路径上

• 注意：定长编码可以由完整的霍夫曼树表示，并且显然具有前缀属性

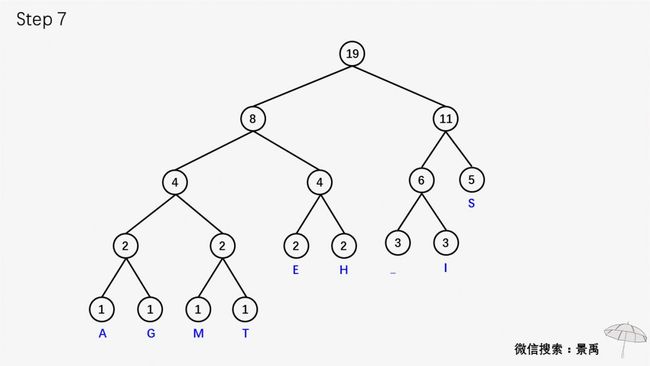
有了霍夫曼编码树的特性，我们也知道了霍夫曼树的构造过程，最后再给大家看一个霍夫曼编码及霍夫曼树构造的完整示例。

示例：建立消息 This is his message 的一颗赫夫曼编码树。

左右滑动查看赫夫曼编码的编码过程。

建立赫夫曼树（可以对照着上面的示例看代码）

htTree * buildTree(char *inputString)
{
  //计算字符串中每一个字符出现的次数
  //已知8个bit位可以表示256个字符
  //(256 ASCII 字符)
  int * probability = (int *)malloc(sizeof(int)*256);
  
  //初始化字符出现次数的统计数组
  for(int i=0; i<256; i++)
    probability[i]=0;

  //将每一个字符的ASCII码值作为索引，统计字符出现次数
  for(int i=0; inputString[i]!='\0'; i++)
    probability[(unsigned char) inputString[i]]++;

  //使用优先队列存储树中的结点
  pQueue * huffmanQueue;
  initPQueue(&huffmanQueue);

  //为字符串中的每一个字符创建一个结点，相当于初始化森林
  for(int i=0; i<256; i++)
    if(probability[i]!=0)
    {
      htNode *aux = (htNode *)malloc(sizeof(htNode));
      aux->left = NULL;
      aux->right = NULL;
      aux->symbol = (char) i;
      
      addPQueue(&huffmanQueue,aux,probability[i]);
    }

  //释放字符出现次数的统计数组，因为优先队列中已经存储了，不需要了
  free(probability);

  //按照赫夫曼树创建步骤创建赫夫曼树
  while(huffmanQueue->size!=1)
  {
    //取出优先队列中权值最小的两个节点，并将它们的权值相加
    int priority = huffmanQueue->first->priority;
    priority+=huffmanQueue->first->next->priority;
    
    //优先队列中的权值最小的两个元素出队并保存
    htNode *left = getPQueue(&huffmanQueue);
    htNode *right = getPQueue(&huffmanQueue);

    //创建一个新结点作为出队的两个节点的父亲节点
    htNode *newNode = (htNode *)malloc(sizeof(htNode));
    newNode->left = left;
    newNode->right = right;
  
    //将新结点的值入队
    addPQueue(&huffmanQueue,newNode,priority);
  }

  //创建树根节点，并将优先队列中最后一个值赋给根结点
  htTree *tree = (htTree *) malloc(sizeof(htTree));

  tree->root = getPQueue(&huffmanQueue);
  
  return tree;
}

得到赫夫曼树之后，我们就可以得到字符的赫夫曼编码了。

计算字符的赫夫曼编码并建表：

hlTable * buildTable(htTree * huffmanTree)
{
  //初始化赫夫曼表
  hlTable *table = (hlTable *)malloc(sizeof(hlTable));
  table->first = NULL;
  table->last = NULL;
  
  //辅助变量
  char code[256];
  //k 记录遍历过程中的层数
  int k=0;

  //遍历赫夫曼树并计算字符编码
  traverseTree(huffmanTree->root,&table,k,code);
  return table;
}

有了赫夫曼码表之后，就可以对输入的字符串进行编码和解码了。

字符串编码：

void encode(hlTable *table, char *stringToEncode)
{
  hlNode *traversal;
  
  printf("\nEncoding\nInput string : %s\nEncoded string : \n",stringToEncode);

  //对字符串的每一个字符遍历赫夫曼码表
  //当在码表中遇到字符，则输出对应的字符编码
  for(int i=0; stringToEncode[i]!='\0'; i++)
  {
    traversal = table->first;
    while(traversal->symbol != stringToEncode[i])
      traversal = traversal->next;
    printf("%s",traversal->code);
  }

  printf("\n");
}

字符串解码：

void decode(htTree *tree, char *stringToDecode)
{
  htNode *traversal = tree->root;

  printf("\nDecoding\nInput string : %s\nDecoded string : \n",stringToDecode);

  //对于消息编码的每一个bit位，遍历赫夫曼树并进行解码操作
  //从赫夫曼的根结点开始，遇到0则走左子树
  //遇到1则走右子树
  for(int i=0; stringToDecode[i]!='\0'; i++)
  {
    if(traversal->left == NULL && traversal->right == NULL)
    {
      printf("%c",traversal->symbol);
      traversal = tree->root;
    }
    
    if(stringToDecode[i] == '0')
      traversal = traversal->left;

    if(stringToDecode[i] == '1')
      traversal = traversal->right;

    if(stringToDecode[i]!='0'&&stringToDecode[i]!='1')
    {
      printf("The input string is not coded correctly!\n");
      return;
    }
  }

  if(traversal->left == NULL && traversal->right == NULL)
  {
    printf("%c",traversal->symbol);
    traversal = tree->root;
  }

  printf("\n");
}

主要代码就是四个关键的函数，需要注意的是，为了保证权值始终按照降序排列，我们使用了优先队列进行存储权值，一般也可以理解为一个小顶堆。

记得给景禹和赫夫曼大叔顺手点个赞奥，也欢迎你把这篇文章转发给需要的朋友，景禹不胜感激！祝小禹禹们每日进步，学有所成！

推荐阅读：
一个我超喜欢的动态博客系统，五分钟即可部署上线！

如何看待第三方百度云 Pandownload 作者被捕？

作为计算机专业学生，最应该学习的课程前五位是什么？

为什么魂斗罗只有 128KB 却可以实现那么长的剧情？