10、TensorFLow 中的损失函数

一、损失函数相关概念

1、交叉熵

• 刻画了两个概率分布之间的距离，也就是说，交叉熵值越小，两个概率分布越接近
• 通过 p 来表示 q 的交叉熵： H(p,q)=−Σp(xi)logq(xi)H(p, q) = -\Sigma p(x_i)logq(x_i)H(p,q)=−Σp(xi​)logq(xi​)，p 为正确答案的分布，q 为预测的分布，这个log是以e为底的
• 代码示例

p = tf.constant([1.0, 0.0, 0.0])
q = tf.constant([0.88, 0.12, 0.0])

# tf.clip_by_value 函数的作用是：将元素数值限制在指定的范围内，防止一些错误运算
# 具体是：q 中的元素小于 1e-10 则用 1e-10 代替，大于 1.0 则用 1.0 代替
cross_entropy = -p * tf.log(tf.clip_by_value(q, 1e-10, 1.0))    # 逐元素相乘

sess.run(cross_entropy)
>>> array([ 0.12783338,  0.        ,  0.        ], dtype=float32)

2、logits

Softmax/Sigmoid 层归一化到(0, 1)的前一层的加权和($WX+b$)

3、Softmax 激活函数

• softmax：将神经网络的输出(多个标量)映射为一个(0, 1)间概率分布
• logits：下图中的 z1、z2、z3z_1 、z_2 、z_3z1​、z2​、z3​，可使用 tf.nn.softmax(logits) 将其转换为概率分布，所有元素概率之和为 1，每一维彼此不独立
• 适用场景：单标签分类问题，标签为 one-hot 编码，类似 $[1,0,0]$ 这种概率分布，真实概率分布为 tf.nn.softmax(logits) 比如 $[0.8,0.1,0.1]$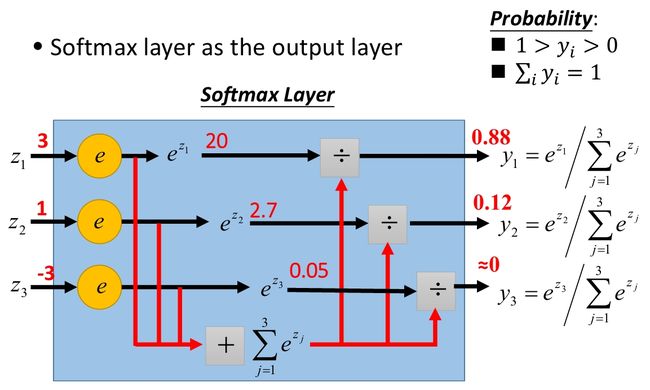
  

4、Sigmoid 激活函数

• sigmoid：将神经网络的输出映射到一个(0, 1)区间
• logits：下图中的 4（可扩展到多个神经元），可使用 tf.nn.sigmoid(logits) 将其转换为概率分布，所有元素概率之和不一定为 1，每一维彼此独立
• 适用场景：多标签分类问题，标签(各种属性：男女、胖瘦、高矮)类似 $[1,0,1]$ 这种概率分布，真实概率分布为 tf.nn.sigmoid(logits) 比如 $[0.8,0.7,0.2]$
  

---

二、分类问题的损失函数

1、使用注意事项

• 第一个注意点是： 函数内部会进行 softmax/sigmoid 运算，所以只需要传入scale 前的 logits 值就可以了
• 第二个注意点是： 使用函数求得的是一个一维的张量(batch 个)，张量中的每个元素代表一个样例中所有元素交叉熵的和，要想得到最终的loss，还需要进行一下reduce_mean 操作，求得一个 batch 的平均损失

2、softmax/sigmoid 函数的作用

• 交叉熵刻画的是两个概率分布之间的距离，然而神经网络的输出却不一定是一个概率分布。所以要借助softmax/sigmoid 函数使得输出变为一个概率分布
• 任何事件发生的概率都在 0 和 1 之间，且总有某一个事件发生(概率的和为 1)。分类问题中可以把一个样例属于某一个类别看成一个概率事件，那么训练数据的正确答案就符合一个概率分布，训练的目的就是：尽量使输出的概率分布符合正确答案的概率分布

3、tf.nn.softmax_cross_entropy_with_logits

a、函数解析

tf.nn.softmax_cross_entropy_with_logits(labels=None, logits=None, dim=-1, name=None)

输入参数：

• labels： one_hot 形式，例如 [1.0, 0.0, 0.0], 注意数据类型为浮点型，可借助 tf.one_hot() 函数来实现
• logits： 经过 softmax 前的值，例如上图中的 [z1,z2,z3]=[3.0,1.0,−3.0][z_1, z_2, z_3] = [3.0, 1.0, -3.0][z1​,z2​,z3​]=[3.0,1.0,−3.0]
• dim： The class dimension. Defaulted to -1 which is the last dimension.

输出：

• 一维的张量(batch 个)，张量中的每个元素代表一个样例中所有元素交叉熵的和

b、代码示例

# 神经网络的输出
logits = tf.constant([3.0, 1.0, -3.0])  

# 正确的标签
y_ = tf.constant([1.0, 0.0, 0.0])

# 神经网络的输出经过 softmax 变换
y = tf.nn.softmax(logits)
>>> array([ 0.88,  0.12,  0.0], dtype=float32)

# 计算交叉熵(得到一个一维张量)  
cross_entropy = -y_*tf.log(tf.clip_by_value(y, 1e-10, 1.0)) 
>>> array([ 0.12783338,  0.        ,  0.        ], dtype=float32)

# 计算一个样例中所有元素交叉熵的和
cross_entropy_sum = tf.reduce_sum(cross_entropy, axis=-1)
>>> 0.12783338

*********************************************************************
以上模拟了tf.nn.softmax_cross_entropy_with_logits()函数的具体实施过程
*********************************************************************

# 使用tf.nn.softmax_cross_entropy_with_logits()函数直接计算神经网络的输出结果交叉熵的和
cross_entropy2 = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=logits)
>>> 0.12783338

# 上面只是一个样例的交叉熵的和，若想要求得一个 batch 上的交叉熵和的平均值(即loss)，还需执行下面的这句
loss = tf.reduce_mean(cross_entropy2) 

c、tf.nn.sparse_softmax_cross_entropy_with_logits

• tf.nn.softmax_cross_entropy_with_logits()的易用版本：此函数的labels 不用转换为one_hot 的形式
• labels 的取值范围是：[0, num_classes)

---

4、tf.nn.sigmoid_cross_entropy_with_logits

a、函数解析

tf.nn.sigmoid_cross_entropy_with_logits(labels=None, logits=None, name=None)

输入参数：

• labels: A Tensor of the same type and shape as logits，取值为 0 或 1
• logits: 经过 sigmoid 前的值

输出：

• A Tensor of the same shape as logits with the componentwise logistic losses.

注意：

• logits and labels must have the same type and shape

计算公式：

• for brevity, let x = logits, z = labels ，正确答案的分布为：[z, 1 - z]；预测的分布为：[sigmoid(x), 1 - sigmoid(x)]
• The logistic loss is z * -log(sigmoid(x)) + (1 - z) * -log(1 - sigmoid(x))

b、代码示例

# 神经网络的输出(3 个样例)
logits = tf.constant([4.0, 2.0, -2.0])  

# 正确的标签
y_ = tf.constant([1.0, 1.0, 0.0])

# 计算每个样例的交叉熵损失
cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y_, logits=logits)
>>> array([ 0.01814993,  0.126928  ,  0.126928  ], dtype=float32)

# 计算一个 batch 上的交叉熵和的平均值(即loss)
loss = tf.reduce_mean(cross_entropy2) 
>>> 0.090668641

c、tf.nn.weighted_cross_entropy_with_logits( targets, logits, pos_weight, name=None)

• 比tf.nn.sigmoid_cross_entropy_with_logits()函数多了一个pos_weight 参数
• pos_weight的作用： allows one to trade off recall and precision by up- or down-weighting the cost of a positive error relative to a negative error.
• 计算公式：pos_weight * z * -log(sigmoid(x)) + (1 - z) * -log(1 - sigmoid(x))，

---

三、回归问题的损失函数

1、Mean Squared Error(MSE)

• MSE(y_,y)=1n∑i=1n(y_(i)−y(i))2MSE(y_{\_}, y)= \frac{1}{n} \sum_{i=1}^{n}(y_{\_}^{(i)}-y^{(i)})^{2}MSE(y_​,y)=n1​∑i=1n​(y_(i)​−y(i))2
• 其中 y_(i)y_{\_}^{(i)}y_(i)​ 为一个batch 中第 i 个数据的正确答案，而 y(i)y^{(i)}y(i) 为神经网络给出的预测值
• 欧氏损失前可增加 Sigmoid 操作进行归一化，相应的输出标签也归一化到 $[0,1]$，避免梯度溢出

2、TF 中实现 MSE

• mse = tf.reduce_mean(tf.square(y_ - y))

---

四、其它损失函数

• Center loss
  • 在最大化类间距的同时，最小化类内距，从而使得特征具备更强的判别能力，一般配合 softmax loss 使用
  • 其中 xix_ixi​ 为倒数第二层的特征值，cyic_{y_i}cyi​​ 为 第 yiy_iyi​ 类所有深度特征的均值（“中心”），一般随机初始化为 xix_ixi​ 相同的维度，然后通过训练不断更新其值（类中心）
    
• Large-Margin Softmax loss
  • 在Softmax Loss 中通过约束权重矩阵的夹角引入Margin 正则
• Triplet loss
  
• Focal loss
  • 思想：用一个权重条件函数去降低易分样本对损失的贡献
  • 使用场景：解决 one-stage 的目标检测中背景样本和前景样本的不平衡问题
  • Focal loss：FL(pt)=−(1−pt)γlog(pt)FL(p_t) = -(1 - p_t)^{\gamma} log(p_t)FL(pt​)=−(1−pt​)γlog(pt​)
    
    

---

五、参考资料

1、https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits
2、Tensorflow基础知识—损失函数详解