TensorFlow学习笔记(五)——损失函数
前言:
神经网络模型的效果以及优化的目标是通过损失函数(loss function)来定义的。本章将学习适用于分类问题和回归问题的经典损失函数。
分类问题和回归问题是监督学习的两大种类。
一、分类问题中的损失函数
分类问题希望解决的是将不同的样本分到事先定义好的类别中,例如手写体数字识别问题可以被归纳成一个十分类问题。手写体数字识别问题可以被看成将一张包含了数字的图片分类到0〜9这10个数字中。通过神经网络解决多分类问题最常用的方法是设置n个输出节点,其中n为类别的个数。
对于每一个样例,神经网络可以得到的一个n维数组作为输出结果,数组中的每一个维度(也就是每一个输出节点)对应一个类别。在理想情况下,如果一个样本属于类别k,那么这个类别所对应的输出节点的输出值应该为1,而其他节点的输出都为0。以识别数字1为例,神经网络模型的输出结果越接近[0,1,0,0,0,0,0,0,0,0]越好。那么如何判断一个输出向量和期望的向量有多接近呢?交叉熵(cross entropy)是常用的评判方法之一。交叉熵刻画了两个概率分布之间的距离,它是分类问题中使用比较广的一种损失函数。交叉熵是一个信息论中的概念,给定两个概率分布![]() 和
和![]() ,通过
,通过![]() 来表示
来表示![]() 的交叉熵为:
的交叉熵为:
注意交叉熵刻画的是两个概率分布之间的距离,然而神经网络的输出却不一定是一个概率分布。概率分布刻画了不同事件发生的概率。当事件总数是有限的情况下,概率分布函数![]() 满足:
满足:
那么如何将神经网络前向传播得到的结果也变成 概率分布呢? Softmax回归就是一个非常常用的方法。
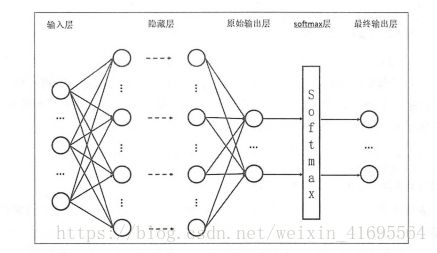
Sofmax回归本身可以作为一个学习算法来优化分类结果,但在TensorFlow中,Softmax 回归的参数被去掉了,它只是一层额外的处理层,将神经网络的输出变成一个概率分布。 下图展示了加上了 Softmax回归的神经网络结构图:
假设原始的神经网络输出为![]() ,那么经过Softmax回归处理之后的输出为:
,那么经过Softmax回归处理之后的输出为:
从以上公式中可以看出,原始神经网络的输出被用作置信度来生成新的输出,而新的输出满足概率分布的所有要求。这个新的输出可以理解为经过神经网络的推导,一个样例为不同类别的概率分别是多大。这样就把神经网络的输出也变成了一个概率分布,从而可以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离了。
下面将给出两个具体样例来直观地说明通过交叉熵可以判断预测答案和真实答案之间的距离:
假设有一个三分类问题,某个样例的正确答案是(1,0,0)。某模型经过Softmax回归之后的预测答案是(0.5,0.4,0.1),那么这个预测和正确答案之间的交叉熵为:
![]()
如果另外一个模型的预测是(0.8,0.1,0.1),那么这个预测值和真实值之间的交叉熵是:
![]()
从直观上可以很容易地知道第二个预测答案要优于第一个。通过交叉熵计算得到的结果也是一致的(第二个交叉熵的值更小)。我们经常通过TensorFlow实现过交叉熵,其代码实现如下:
cross_entropy = -tf.reduce_mean( y_ * tf.log(tf.clip_by_value(y,le-10, 1.0)))其中,y_代表正确结果,y代表预测结果。这一行代码包含了四个不同的TensorFlow运算。为了了了解这些TensorFlow运算,我们来看下面:
#coding=gbk
###################################
######### 作者:行歌 ############
######### 时间:2018.5.3 ########
###### email:[email protected] ##
###################################
import tensorflow as tf
#载入TensorFlow库
y_ = tf.constant([[1,0,0],[1,0,0]],tf.float32)
y = tf.constant([[0.5,0.4,0.1],[0.8,0.1,0.1]])
middle_value = tf.log(tf.clip_by_value(y, 1e-10, 1.0))
# tf.log函数,这个函数完成了对张量中所有元素依次求对数的功能
middle_result = tf.reduce_mean( y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)) )
# 将两个矩阵通过“*”操作相乘。这个 操作不是矩阵乘法,而是元素之间直接相乘
# 矩阵乘法需要使用tf.matmul函数来完成
cross_entropy = -tf.reduce_mean(y_*tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
# 其中y_代表正确结果,y代表预测结果
# 通过tf.clip_by_value函数可以将一个张量中的数值限制在一个范围之内,这样可以避免一些运算错误(比如logO是无效的)
# 小于 1e-10的数都被换成了 1e-10,而大于1.0的数都被换成了1.0
# 这样通过tf.clip_by_value函数就可以保证在进行log运算时,不会出现log0这样的错误或者大于1的概率
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
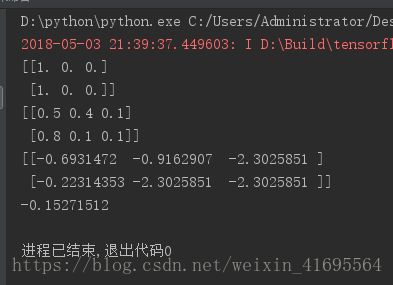
print(sess.run(y_))
print(sess.run(y))
print(sess.run(middle_value))
print(sess.run(middle_result))
运行程序,结果如下:
二、 回归问题中的损失函数
与分类问题不同,回归问题解决的是对具体数值的预测。比如房价预测、销量预测等都是回归问题。这些问题需要预测的不是一个事先定义好的类别,而是一个任意实数。解决回归问题的神经网络一般只有一个输出节点,这个节点的输出值就是预测值。对于回归问题,最常用的损失函数是均方误差(MSE, mean squared error) 。它的定义如下:
其中![]() 为一个batch中第i个数据的正确答案,而
为一个batch中第i个数据的正确答案,而![]() 为神经网络给出的预测值。以下代码展示了如何通过TensorFlow实现均方误差损失函数,其中y代表了神经网络的输出答案,y_代表了标准答案:
为神经网络给出的预测值。以下代码展示了如何通过TensorFlow实现均方误差损失函数,其中y代表了神经网络的输出答案,y_代表了标准答案:
mse = tf.reduce_mean(tf.square(y_ - y))参考文献:
[1] 郑泽宇著 《TensorFlow实战Google深度学习框架》
[2] 黄文坚著 《TensorFlow实战》