详谈二叉树3—python数据结构之线索二叉树(线索链表)—创建、遍历

具有n个结点的二叉链表中，有n+1个空指针。
将二叉链表中的空指针域利用起来，指向其前驱结点和后继结点，这就将二叉树编程了线索二叉树。

1.定义

线索:将二叉链表中的空指针域指向前驱结点和后继结点的指针被称为线索。

线索化:使二叉链表中结点的空链域存放其前驱或后继信息的过程称为线索化；

线索链表:加上线索的二叉链表称为线索链表（或线索二叉树）

2.分类

二叉树的遍历方式有4种，故有4种意义下的前驱和后继，相应的有4种线索二叉树：

1. 前序线索二叉树
2. 中序线索二叉树
3. 后序线索二叉树
4. 层序线索二叉树

3.创建

以中序线索二叉树为例讲解线索二叉树的创建。

中序线索二叉树的创建

1.二叉树的中序序列为：D G B A E C F

2.将二叉树线索化，空的左指针指向前驱结点，空的右指针指向后继结点

上图中：
G的左空指针指向其前驱结点D，右空指针指向其后继结点B
B的右空指针指向其后继结点A
E的左空指针指向其前驱结点A，右空指针指向其后继结点C
F的左空指针指向其前驱结点C，右空指针指向其后继结点空

这样就很方便找到中序序列的前驱和后继了。

线索化的具体过程就是在二叉树的遍历中修改空指针。

线索化具体实现

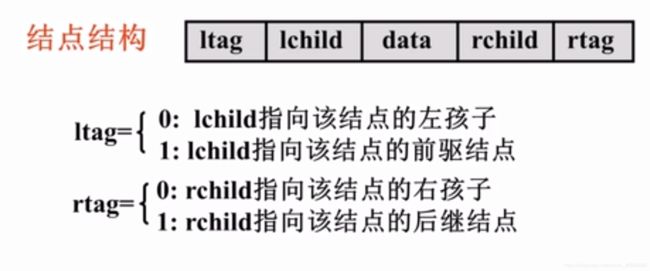
1.结点结构的改变

如果只是在原二叉树的基础上利用空结点，那么就存在着这么一个问题：我们如何知道某一结点的lchild是指向他的左孩子还是指向前驱结点？rchild是指向右孩子还是后继结点？显然我们要对他的指向增设标志来加以区分。

因此，我们在每一个结点都增设两个标志域Itag和rtag，它们只存放0或1的布尔型变量，占用的空间很小。于是结点的结构如图所示。

2.建立过程

我们设置
pre指针，永远指向遍历当前结点的前一个结点

1. 建立二叉链表，将每个结点的左右标志设置为0；

2. 遍历二叉链表，建立线索；
   2.1如果当前结点为空，则空操作返回；
   2.2对当前结点p的左子树建立线索即先线索化左子树；
   2.3对根结点p建立线索；

   • 若p没有左孩子，则为p加上前驱线索即Itag=1以及把左孩子的指针Ichild指向pre(相对当前结点的前驱结点)。
   • 若pre没有右孩子，则为pre加上后继线索即rtag=1以及把pre右孩子的指针rchild指向当前结点p(p相对pre结点为后继结点)。
   • 把当前结点赋给pre，完成后续的递归遍历线索化。p指针按照中序遍历的过程不断移动

   2.4对P的右子树建立线索即线索化右子树；

python实现化：

class TreeNode(object):#创建线索链表的结点
    def __init__(self,val=None):
        self.val = val
        self.left = None
        self.right = None
        """
        在树结点的基础上增加类型指针
        如果left_type==0 表示指向该结点的左孩子;如果是1，则表示指向该结点的前驱结点
        如果right_type==0 表示指向该结点的右孩子;如果是1，则表示指向该结点的后继结点
        初始化每个结点的左右标志left_type、right_type为0
        """
        self.left_type = 0
        self.right_type = 0
class ThreadedBinaryTree(object):  # 创建中序线索二叉树
    def __init__(self):
        self.root=None
        # 在递归进行线索化，总是保留前一个结点

        self.pre = None  # 为实现线索化，需要创建给指向当前结点的前驱结点指针

    # 中序线索二叉树结点
    def threaded_node(self, node):  # node:就是当前需要线索化的结点
        if node is None:
            return
        # 先线索化左子树
        self.threaded_node(node.left)

        # 线索化当前结点，处理当前结点的前驱结点
        if node.left is None:  # 如果当前结点没有左孩子即左子结点为空
            node.left = self.pre  # 让当前结点的左指针指向前驱结点
            node.left_type = 1  # 修改当前结点的左指针类型为1

        # 处理当前结点的后继结点
        if self.pre and self.pre.right is None:
            self.pre.right = node  # 让前驱结点的右指针指向当前指针
            self.pre.right_type = 1  # 修改前驱结点的右指针类型为1
        self.pre = node  # 每处理一个结点后，保证当前结点是下一个结点的前驱结点

        # 线索化右子树
        self.threaded_node(node.right)

以下面的例子验证以下线索化是否正确

class TreeNode(object):#创建线索链表的结点
    def __init__(self,val=None):
        self.val = val
        self.left = None
        self.right = None
        """
        在树结点的基础上增加类型指针
        如果left_type==0 表示指向该结点的左孩子;如果是1，则表示指向该结点的前驱结点
        如果right_type==0 表示指向该结点的右孩子;如果是1，则表示指向该结点的后继结点
        初始化每个结点的左右标志left_type、right_type为0
        """
        self.left_type = 0
        self.right_type = 0

class ThreadedBinaryTree(object):  # 创建中序线索二叉树
    def __init__(self):
        self.root=None
        # 在递归进行线索化，总是保留前一个结点

        self.pre = None  # 为实现线索化，需要创建给指向当前结点的前驱结点指针

    # 中序线索二叉树结点
    def threaded_node(self, node):  # node:就是当前需要线索化的结点
        if node is None:
            return
        # 先线索化左子树
        self.threaded_node(node.left)

        # 线索化当前结点，处理当前结点的前驱结点
        if node.left is None:  # 如果当前结点没有左孩子即左子结点为空
            node.left = self.pre  # 让当前结点的左指针指向前驱结点
            node.left_type = 1  # 修改当前结点的左指针类型为1

        # 处理当前结点的后继结点
        if self.pre and self.pre.right is None:
            self.pre.right = node  # 让前驱结点的右指针指向当前指针
            self.pre.right_type = 1  # 修改前驱结点的右指针类型为1
        self.pre = node  # 每处理一个结点后，保证当前结点是下一个结点的前驱结点

        # 线索化右子树
        self.threaded_node(node.right)

    # 中序遍历测试
    def inorder(self,node):
        """用递归实现中序遍历"""
        if node is None:
            return
        self.inorder(node.left)
        print(node.val, end=" ")
        self.inorder(node.right)
if __name__ == '__main__':
   # 验证中序线索化是否成功
   # 手动创建一个二叉树
   t=ThreadedBinaryTree()
   t1 = TreeNode(2)
   t2 = TreeNode(3)
   t3 = TreeNode(6)
   t4 = TreeNode(8)
   t5 = TreeNode(10)
  
   t1.left = t2
   t1.right = t3
   t2.left = t4
   t2.right = t5
  
   print("原来的二叉树中序遍历为：")
   t.inorder(t1)
   # 线索化二叉树
   t.threaded_node(t1)
   # 测试：以值为10 的结点来测试
   left_node = t5.left
   print()
   print("10 的前驱结点是：%d" % left_node.val)  
   right_node = t5.right
   print("10 的后继结点是：%d" % right_node.val)

结果：

原来的二叉树中序遍历为：
8 3 10 2 6 
10 的前驱结点是：3
10 的后继结点是：2

Process finished with exit code 0

说明中序线索二叉树已成功

4.作用

线索二叉树将树转换成线性链表。将遍历信息在首次遍历时线索化，则可以在需要时直接获得结点的前驱和后继，节省时间。

–>

4.1中序线索链表查找后继

1. 如果结点p的右标志为1，则表明该结点的右指针是线索即它的后继结点；
2. 如果结点p的右标志为0，则表明该结点有右孩子。根据中序遍历的操作定义，它的后继结点应该是遍历其右子树时第一个访问的结点，即右子树的最左下结点。

4.2中序线索链表的遍历

思路:

线索化二叉树后，各个结点结构指向有变化，因此原来的遍历方式不一样，可以通过线性方式遍历。

对于中序遍历来说，先查找线索链表的第一个节点，也就是最左方向上的最后一个节点，然后如果有右线索先寻找后继节点，查找到断线索（有右孩子啦）就往下找一个右节点，继续这样摸下去，其实说到底就是有线索先按线索找（注意线索上的节点是需要访问的），等到线索断了就往下找右孩子节点。

class TreeNode(object):  # 创建线索链表的结点
    def __init__(self, val=None):
        self.val = val
        self.left = None
        self.right = None
        """
        在树结点的基础上增加类型指针
        如果left_type==0 表示指向该结点的左孩子;如果是1，则表示指向该结点的前驱结点
        如果right_type==0 表示指向该结点的右孩子;如果是1，则表示指向该结点的后继结点
        初始化每个结点的左右标志left_type、right_type为0
        """
        self.left_type = 0
        self.right_type = 0


class ThreadedBinaryTree(object):
    def __init__(self):
        self.root = None
        # 在递归进行线索化，总是保留前一个结点

        self.pre = None  # 为实现线索化，需要创建给指向当前结点的前驱结点指针

    # 中序线索二叉树结点
    def threaded_node(self, node):  # node:就是当前需要线索化的结点
        if node is None:
            return
        # 先线索化左子树
        self.threaded_node(node.left)

        # 线索化当前结点，处理当前结点的前驱结点
        if node.left is None:  # 如果当前结点没有左孩子即左子结点为空
            node.left = self.pre  # 让当前结点的左指针指向前驱结点
            node.left_type = 1  # 修改当前结点的左指针类型为1

        # 处理当前结点的后继结点
        if self.pre and self.pre.right is None:
            self.pre.right = node  # 让前驱结点的右指针指向当前指针
            self.pre.right_type = 1  # 修改前驱结点的右指针类型为1
        self.pre = node  # 每处理一个结点后，保证当前结点是下一个结点的前驱结点

        # 线索化右子树
        self.threaded_node(node.right)

    # 中序遍历线索化二叉树
    def threaded_in_order(self, node):
        if node is None:
            return
        temp_node = node
        while temp_node:
            # 循环的找到left_type=1的结点，第一个找到就是值为8的结点
            # 后面随着遍历而变化，因为当left_type=1时，说明该结点是按照线索化处理后的有效结点
            while temp_node.left_type == 0:  # 从根结点开始向左找，找到第一个1停止
                temp_node = temp_node.left
            # 打印当前这个结点
            print(temp_node.val, end=" ")
            # 如果当前结点的右指针指向的是后继结点，就一直输出
            while temp_node.right_type == 1:
                # 获取到当前结点的后继结点
                temp_node = temp_node.right
                print(temp_node.val, end=" ")
            # 如果不等于1了，就替换这个遍历的结点
            temp_node = temp_node.right

        # 中序遍历测试

    def in_order(self, node):
        if node is None:
            return
        self.in_order(node.left)
        print(node.val, end=' ')
        self.in_order(node.right)


if __name__ == '__main__':
    t = ThreadedBinaryTree()
   
    # 手动创建结点--只是为了更好测试线索化有没有成功
    t1 = TreeNode(1)
    t2 = TreeNode(3)
    t3 = TreeNode(6)
    t4 = TreeNode(8)
    t5 = TreeNode(10)
    t6 = TreeNode(14)
    t1.left = t2
    t1.right = t3
    t2.left = t4
    t2.right = t5
    t3.left = t6
    print("原来的二叉树中序遍历为：")
    t.in_order(t1)
    # 线索化二叉树
    t.threaded_node(t1)
    print()
    print("线索化二叉树的中序遍历结果为：")
    t.threaded_in_order(t1)

结果：

原来的二叉树中序遍历为：
8 3 10 1 14 6 
线索化二叉树的中序遍历结果为：
8 3 10 1 14 6 
Process finished with exit code 0

参考：
B站视频
大话数据结构
https://blog.csdn.net/storyfull/article/details/103744339