「数据结构基础」数组与特殊矩阵
目录
- 数组
- 一维数组
- 二维数组与多维数组
- 特殊矩阵的压缩存储
- 对角矩阵
- 代码
- 对称矩阵
- 第i行第j列的元素在数组中的哪个位置
- 代码
- 总结
- 稀疏矩阵
- 代码
- 稀疏矩阵还有一种表现形式,称为十字链表
数组
数组就是顺序表,只不过在C/C++里功能少一点,只有赋值和取值。
数组都很熟,在这里主要说一点存储结构的事。
一维数组
二维数组与多维数组
二维数组的存储结构有两种形式,分别为按行优先存放与按列优先存放。
按行优先存放,就是第1行先放元素,第1行放满了再放第2行,第3行,第4行……
就像这样
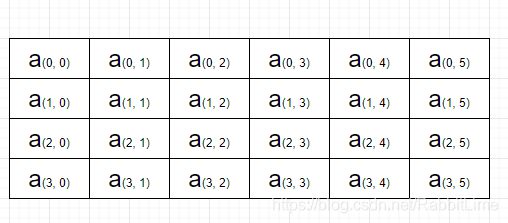
那么按列优先存放,显然就是一列一列的放
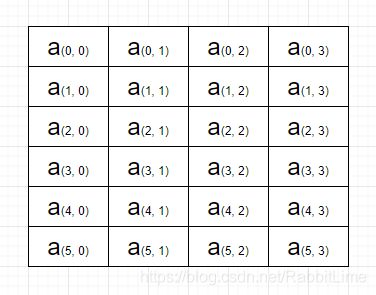
不过学过矩阵的都知道,行是可以看成列的,列也是可以看成行的,怎么看其实无所谓。
int Matrix[3][3] = { {1,2,3},{4,5,6},{7,8,9} };
一个二维数组,本质上是多个数组本身组成的一个数组。
注意上面两张图的下标变化规律,按行优先存放的是右边的下标(列数)先变化,按列优先存放的是左边的下标(行数)先变化。
而二维数组在内存中是遵循按行优先存放的。*(*(Matrix) + 1)的值是2,而不是4。
推广至多维数组也一样,多维数组也是数组套着数组,在内存中也是按行优先存放,最右边的下标先变化。
特殊矩阵的压缩存储
矩阵,特别是高阶矩阵,需要大量的内存空间。
其中有一些特殊的矩阵,它们的元素分布是有规律的,
如果我们利用好这些规律,就可以对特殊矩阵进行压缩存储。
这样就可以节省将近一半甚至更多的内存空间的消费。
接下来讲三个例子。
对角矩阵
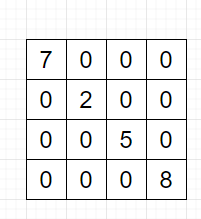
对角矩阵(Diagonal Matrix)就是只有主对角线有元素。
如果我们使用二维数组来存储这个矩阵,就需要16个int的内存空间。
但是其实我们只需要一个长度为4的一维数组就能把它搞定。
用户取第i行第j列,若i = j,就到数组里取,否则就都是0。
接下来上代码。
代码
DiagonalMatrix.h:
#pragma once
#include DiagonalMatrix.cpp:
#include "DiagonalMatrix.h"
DiagonalMatrix::DiagonalMatrix(const int n)
{
N = n;
Data = new double[N]{};
}
DiagonalMatrix::DiagonalMatrix(const DiagonalMatrix& otherMatrix)
{
N = otherMatrix.N;
Data = new double[N]{};
for (int i = 0; i < N; i++)
Data[i] = otherMatrix.Data[i];
}
DiagonalMatrix::~DiagonalMatrix()
{
delete[] Data;
}
DiagonalMatrix::DiagonalMatrix_Row DiagonalMatrix::operator[](const int i)
{
return DiagonalMatrix_Row(i, N, Data);
}
std::ostream& operator<<(std::ostream& os, const DiagonalMatrix& dm)
{
double temp;
for (int i = 0; i < dm.N; i++)
{
for (int j = 0; j < dm.N; j++)
{
temp = (i == j) ? dm.Data[i] : 0;
os << '\t' << temp;
}
os << std::endl;
}
return os;
}
double& DiagonalMatrix::DiagonalMatrix_Row::operator[](const int j)
{
if (i >= N || j >= N || i < 0 || j < 0)
throw std::out_of_range("Index is out of range!");
Zero = 0;
return (i == j)? Data[i] : Zero;
}
对称矩阵
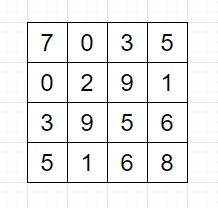
对称矩阵(Symmetric Matrix)就像这样,上三角与下三角根据主对角线对称分布。
既然第i行第j列的值跟第j行第i列的值都一样,
那么我们只需要存储其中一个三角加上主对角线元素不就好了吗?
当用户访问到另一个三角的时候,
给他指向到对应对称位置就好了。
对于一个n阶矩阵,我们容易得到,其中一个三角加上主对角线元素,一共有n*(n+1)/2个。
我们将n*(n+1)/2个元素存入一个一维数组,构成顺序存储结构,
当用户调用时,通过计算得到第i行第j列的元素在数组中的位置,就可以执行查询和修改的操作。
那么选择哪一个三角呢?
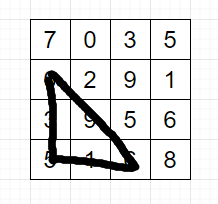
当然是下三角比较合适,下三角中,每一行拥有的元素个数随行数增加而增加,这样便于我们计算。
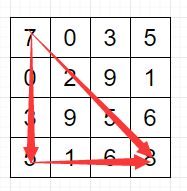
第i行第j列的元素在数组中的哪个位置
不难得出,
当第i行第j列的元素在主对角线上时,i = j。
当第i行第j列的元素在下三角上时,i > j。
当第i行第j列的元素在上三角上时,i < j。
假设i = 3,那么第4行上方的3行:
第1行只有1个元素,
第2行有2个元素,
第3行有3个元素,
那么前i行一共有1 + 2 + 3 + ... + i = i * (i + 1) / 2个元素。
第i行第j列,就是数组中第i * (i + 1) / 2 + j + 1个元素,即为Array[i * (i + 1) / 2 + j]。
那么第j行第i列的元素将对应到什么位置?
很简单,将i和j换换就好,即为Array[j * (j + 1) / 2 + i]。
知道了这些,就有了查询操作和赋值操作的依据,接下来上代码。
代码
SymmetricMatrix.h:
#pragma once
#include SymmetricMatrix.cpp:
#include "SymmetricMatrix.h"
SymmetricMatrix::SymmetricMatrix(const int n)
{
N = n;
Data = new double[N * (N + 1) / 2]{};
}
SymmetricMatrix::SymmetricMatrix(const SymmetricMatrix& otherMatrix)
{
N = otherMatrix.N;
Data = new double[N * (N + 1) / 2]{};
for (int i = 0; i < N * (N + 1) / 2; i++)
Data[i] = otherMatrix.Data[i];
}
SymmetricMatrix::~SymmetricMatrix()
{
delete[] Data;
}
SymmetricMatrix::SymmetricMatrix_Row SymmetricMatrix::operator[](const int i)
{
return SymmetricMatrix_Row(i, N, Data);
}
std::ostream& operator<<(std::ostream& os, const SymmetricMatrix& sm)
{
double temp;
for (int i = 0; i < sm.N; i++)
{
for (int j = 0; j < sm.N; j++)
{
temp = (i < j) ? sm.Data[j * (j + 1) / 2 + i] : sm.Data[i * (i + 1) / 2 + j];
os << '\t' << temp;
}
os << std::endl;
}
return os;
}
double& SymmetricMatrix::SymmetricMatrix_Row::operator[](const int j)
{
if (i >= N || j >= N || i < 0 || j < 0)
throw std::out_of_range("Index is out of range!");
return (i < j) ? Data[j * (j + 1) / 2 + i] : Data[i * (i + 1) / 2 + j];
}
总结
对特殊矩阵的压缩存储,重点在于查询操作的改造。
稀疏矩阵
稀疏矩阵(Sparse Matrix)是相对来说比较重要的。
完成稀疏矩阵的压缩存储,除了改造查询操作,还要改变存储结构。
稀疏矩阵的定义是:矩阵里很多元素都是0,非零元素占比很小,不得超过5%。
相比二维数组,如果只存储那些非零元素,内存占用将会小很多。
同时,这些非零元素的分布是无序的,我们需要一个新的存储模式。
就是将非零元素的行下标、列下标、值打包成一个三元组(3-tuples Node),
并将这些三元组制成链表。
查询一个位置的时候,看看这些三元组哪个是这个位置的,
如果都不是,那就返回0。
给一个位置的元素赋值,就看看这儿是不是非零元素的三元组。
是的话就把它改了,不是的话再加一个三元组。
需要注意的是,
稀疏矩阵是有实际用途的,所以它要求三元组链表必须是按行优先排列的有序表。
所以应找到合适的位置插入。
代码
SparseMatrix.h:
#pragma once
#include SparseMatrix.cpp:
#include "SparseMatrix.h"
ThreeTupleNode::ThreeTupleNode(const int i, const int j, const double data)
{
I = i;
J = j;
Data = data;
}
ThreeTupleNode::ThreeTupleNode(const ThreeTupleNode& otherNode)
{
I = otherNode.I;
J = otherNode.J;
Data = otherNode.Data;
}
SparseMatrix::SparseMatrix(const int rows, const int columns)
{
Rows = rows;
Columns = columns;
N = rows * columns * 0.05;
Nodes = new ThreeTupleNode[N];
}
SparseMatrix::SparseMatrix(const SparseMatrix& otherMatrix)
{
Rows = otherMatrix.Rows;
Columns = otherMatrix.Columns;
N = otherMatrix.N;
Count = otherMatrix.Count;
Nodes = new ThreeTupleNode[N];
for (int i = 0; i < Count; i++)
Nodes[i] = ThreeTupleNode(otherMatrix.Nodes[i]);
}
SparseMatrix::~SparseMatrix()
{
delete[] Nodes;
}
double SparseMatrix::Get(const int i, const int j) const
{
ThreeTupleNode* temp = Find(i, j);
return (temp == nullptr) ? 0.0 : temp->Data;
}
void SparseMatrix::Set(const int i, const int j, const double value)
{
if (i < 0 || i >= N || j < 0 || j >= N)
return;
ThreeTupleNode* temp = Find(i, j);
if (temp == nullptr)
{
if (Count >= N)
return;
int tempindex = -1;
for (int k = 0; k < Count; k++)
if (Nodes[k].I > i || (Nodes[k].I == i && Nodes[k].J > j))
{
tempindex = k;
break;
}
if (tempindex == -1)
Nodes[Count++] = ThreeTupleNode(i, j, value);
else
{
for (int k = Count - 1; k >= tempindex; k--)
Nodes[k + 1] = Nodes[k];
Nodes[tempindex] = ThreeTupleNode(i, j, value);
Count++;
}
}
else
temp->Data = value;
}
void SparseMatrix::Trans()
{
int temp;
for (int i = 0; i < Count; i++)
{
temp = Nodes[i].I;
Nodes[i].I = Nodes[i].J;
Nodes[i].J = temp;
}
}
ThreeTupleNode* SparseMatrix::Find(const int i, const int j) const
{
for (int k = 0; k < Count; k++)
if (Nodes[k].I == i && Nodes[k].J == j)
return &Nodes[k];
return nullptr;
}
std::ostream& operator<<(std::ostream& os, const SparseMatrix& sm)
{
double* temp = new double[sm.Rows * sm.Columns]{};
for (int i = 0; i < sm.Count; i++)
temp[sm.Nodes[i].I * sm.Columns + sm.Nodes[i].J] = sm.Nodes[i].Data;
for (int i = 0; i < sm.Rows; i++)
{
for (int j = 0; j < sm.Columns; j++)
os << '\t' << temp[i * sm.Columns + j];
os << std::endl;
}
delete[] temp;
return os;
}
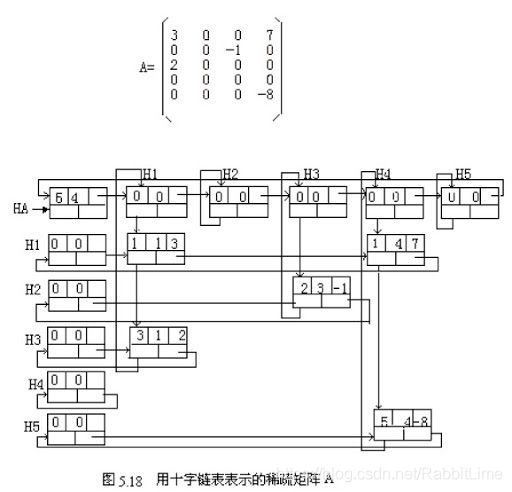
稀疏矩阵还有一种表现形式,称为十字链表
十字链表(orthogonal list)就是把这些三元组排成矩阵。
然后按行给你一行组成一个链表,按列也组成多个链表。
这些链表的Head都在链表之前,都是空表头。
然后看你这个矩阵是行多还是列多,
比如列多,
就把这些列链表的表头也串成一个链表。
比较容易,写起来也比较复杂。
我是懒得写了……明白就好,等用到再写吧。