视觉伺服控制完整解析
视觉伺服控制完整解析
- 视觉伺服控制简介
- 相关符号及概念的说明
- 坐标变换
- 刚体运动
- 相机模型
- 视觉伺服控制理论
- 基于位置的视觉伺服控制
- 基于图像的视觉伺服控制
- 参考文献
视觉伺服控制简介
视觉伺服控制(Visual servo control)简单来说,就是利用计算机视觉得到的数据来控制机器人的移动。一般来说,根据相机的位置不同又分为两种,一种是直接将相机放置在机器人或者机械臂上,另一种是将相机固定在工作空间的某个位置,前者也被称作eye-in-hand。
相关符号及概念的说明
坐标变换
我们都知道三维空间下刚体的运动可以分解为两个部分,平移和旋转。平移没什么好说的,直接用一个向量 t \mathbf{t} t就可以表示。对于旋转,一般情况下,我们都采用一个 3 × 3 3 \times 3 3×3的旋转矩阵来表示。在数学中,旋转矩阵的集合有一个单独的定义,称为特殊正交群,记为
S O ( 3 ) = { R ∈ ℜ 3 × 3 ∣ R R T = I , d e t ( R ) = 1 } SO(3) = \{ \mathbf{R} \in \Re^{3\times 3}\mid \mathbf{R} \mathbf{R}^T = \mathbf{I}, det( \mathbf{R}) = 1\} SO(3)={R∈ℜ3×3∣RRT=I,det(R)=1}这里的 R R R表示旋转矩阵。
当然了,我们都知道,一次旋转只有三个自由度,而旋转矩阵有9个变量,那么很明显存在很多的冗余项。理想情况下只需要三个量就能表示一次旋转,比如欧拉角,但是欧拉角表示法存在万向锁问题,为了解决这个问题,人们又发明了一种新的表示方法,四元数。四元数简单的理解就是用一些规则记录旋转轴和旋转角,这并不是这篇博客的重点,大家感兴趣可以自行搜索。
既然知道了平移和旋转,那么坐标变换就可以写为
a ′ = R a + t \mathbf{a'} = \mathbf{R}\mathbf{a} + \mathbf{t} a′=Ra+t为了写成齐次坐标的形式,引入齐次坐标系,将上式写成如下形式
[ a ′ 1 ] = [ R t 0 T 1 ] [ a 1 ] = T [ a 1 ] \begin{bmatrix} \mathbf{a'} \\1 \end{bmatrix}=\begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix} \begin{bmatrix} \mathbf{a} \\1 \end{bmatrix} =\mathbf{T}\begin{bmatrix} \mathbf{a} \\1 \end{bmatrix} [a′1]=[R0Tt1][a1]=T[a1]类似于旋转矩阵 R \mathbf{R} R,变换矩阵 T \mathbf{T} T也可以组成一个集合,称做特殊欧式群,记为
S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ ℜ 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ ℜ 3 } SE(3)=\{\mathbf{T}=\begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix} \in \Re^{4\times 4}\mid \mathbf{R} \in \mathbf{SO}(3), \mathbf{t}\in \Re^3\} SE(3)={T=[R0Tt1]∈ℜ4×4∣R∈SO(3),t∈ℜ3}机器人的工作空间记为 T = S E ( 3 ) \mathcal{T}=SE(3) T=SE(3)
记点 P P P相对于参考系 x x x的坐标为 x P ^{x}\mathbf{P} xP,参考系 y y y相对于 x x x的旋转矩阵记为 x R y ^x\mathbf{R}_y xRy,同理,坐标原点之间的平移变换记为 x t y ^x\mathbf{t}_y xty,同时包含平移和旋转的变换记为 x x y ^x\mathbf{x}_y xxy。即
x P = x x y ( y P ) = x R y y P + x t y ^x\mathbf{P}= {^x\mathbf{x}_y}(^y\mathbf{P})={^x\mathbf{R}_y} ^y\mathbf{P}+{^x\mathbf{t}_y} xP=xxy(yP)=xRyyP+xty坐标变换之间满足结合律,即
x P = x x y ( y P ) = x x y ( y x z ( z P ) ) = ( x x y ∘ y x z ) ( z P ) = x x z ( z P ) ^x\mathbf{P}= {^x\mathbf{x}}_y(^y\mathbf{P})={^x\mathbf{x}_y} (^y\mathbf{x}_z(^z\mathbf{P}))=({^x\mathbf{x}_y} \circ ^y\mathbf{x}_z)(^z\mathbf{P})={^x\mathbf{x}_z}(^z\mathbf{P}) xP=xxy(yP)=xxy(yxz(zP))=(xxy∘yxz)(zP)=xxz(zP)由简单的刚体运动可知,坐标系变换存在如下关系
x R z = x R y y R z ^x\mathbf{R}_z= {^x\mathbf{R}_y}^y\mathbf{R}_z xRz=xRyyRz x t z = x R y y t z + x t y ^x\mathbf{t}_z= {^x\mathbf{R}_y}^y\mathbf{t}_z+{^x\mathbf{t}_y} xtz=xRyytz+xty对不同参考系,如无特殊说明,均默认为世界参考系,常用参考系角标如下
| 记号 | 对应参考系 |
|---|---|
| e e e | 机器人末端执行机构(end-effector) |
| t t t | 目标物体(target) |
| c i c_i ci | 第 i i i个相机(camera) |
刚体运动
假设考虑末端执行器的工作空间 T ∈ S E ( 3 ) \mathcal{T}\in SE(3) T∈SE(3), P \mathbf{P} P的坐标为 ( x , y , z ) (x, y,z) (x,y,z)。在世界参考系下,对应的角速度和速度为
Ω ( t ) = [ ω x ( t ) , ω y ( t ) , ω z ( t ) ] \mathbf{\Omega}(t)=[\omega_x(t),\omega_y(t),\omega_z(t)] Ω(t)=[ωx(t),ωy(t),ωz(t)] T ( t ) = [ T x ( t ) , T y ( t ) , T z ( t ) ] \mathbf{T}(t)=[T_x(t),T_y(t),T_z(t)] T(t)=[Tx(t),Ty(t),Tz(t)]根据刚体运动学关系,有
x ˙ = z ω y − y ω z + T x \dot{x}=z\omega_y -y\omega_z +T_x x˙=zωy−yωz+Tx y ˙ = x ω z − z ω w + T y \dot{y}=x\omega_z -z\omega_w +T_y y˙=xωz−zωw+Ty z ˙ = y ω x − x ω y + T z \dot{z}=y\omega_x -x\omega_y +T_z z˙=yωx−xωy+Tz写成矩阵形式
P ˙ = Ω × P + T \mathbf{\dot{P}}=\Omega\times \mathbf{P}+\mathbf{T} P˙=Ω×P+T事实上,向量积可以用一个反对称阵(skewsymmetric,也有翻译成斜对称阵)替换,定义
s k ( P ) = [ 0 − z y z 0 − x − y x 0 ] sk(\mathbf{P})=\begin{bmatrix} 0 &-z &y \\ z & 0 & -x \\ -y & x &0 \end{bmatrix} sk(P)=⎣⎡0z−y−z0xy−x0⎦⎤则 P ˙ = − s k ( P ) Ω + T \mathbf{\dot{P}}=-sk(\mathbf{P})\Omega +\mathbf{T} P˙=−sk(P)Ω+T定义速度向量
r ˙ ( t ) = [ T x ( t ) , T y ( t ) , T z ( t ) , ω x ( t ) , ω y ( t ) , ω z ( t ) ] T \mathbf{\dot{r}}(t)=[T_x(t),T_y(t),T_z(t),\omega_x(t),\omega_y(t),\omega_z(t)]^T r˙(t)=[Tx(t),Ty(t),Tz(t),ωx(t),ωy(t),ωz(t)]T及 A ( P ) = [ I 3 ∣ − s k ( P ) ] \mathbf{A(P)}=[I_3 \mid -sk(\mathbf{P})] A(P)=[I3∣−sk(P)]原式可写作
P ˙ = A ( P ) r ˙ \mathbf{\dot{P}}=\mathbf{A(P)}\dot{\mathbf{r}} P˙=A(P)r˙同样的,对速度向量,在不同参考系下的刚体运动有如下关系
r ˙ = [ t Ω ] = [ R e e T − R e e Ω × t e R e e Ω ] \dot{\mathbf{r}}=\begin{bmatrix} \mathbf{t} \\ \mathbf{\Omega} \end{bmatrix} = \begin{bmatrix} \mathbf{R}_e {^e\mathbf{T}}-\mathbf{R}_e {^e\mathbf{\Omega}}\times \mathbf{t}_e \\ \mathbf{R}_e {^e\mathbf{\Omega}} \end{bmatrix} r˙=[tΩ]=[ReeT−ReeΩ×teReeΩ]
相机模型
一般对相机模型的划分大致包括几类,透视投影(perspective projection),正交投影(orthographic projection)和仿射投影(affine projection),正交投影也可以看做仿射投影的特例。其中,最常见的就是透视投影模型。透视模型的一般形式如下:
π ( x , y , z ) = [ u v ] = λ z [ x y ] \pi(x,y,z)=\begin{bmatrix} u \\ v\end{bmatrix}=\frac{\lambda}{z} \begin{bmatrix} x \\ y\end{bmatrix} π(x,y,z)=[uv]=zλ[xy]对相机捕获的图像,我们用 f = [ f 1 , f 2 , . . . , f k ] k ∈ F \mathbf{f}=[f_1,f_2,...,f_k]^k \in \mathcal{F} f=[f1,f2,...,fk]k∈F表示图像特征参数, F \mathcal{F} F为图像特征空间。定义从工作空间到图像特征空间的函数映射如下:
f : T → F \mathbf{f}:\mathcal{T}\rightarrow\mathcal{F} f:T→F
视觉伺服控制理论
关于视觉伺服控制主要有两个问题
- 控制结构是否分层,即视觉系统提供设定点作为机器人控制器的输入,还是视觉控制器直接计算机器人控制器输入。
- 误差是定义在3D参考系下还是2D参考系下
如果控制结构是分层的,则称为dynamic look-and-move,否则称为direct visual servo。如果误差定义在3D参考系,则称为基于位置(position-based),否则称为基于图像(image-based)。因此根据上述两个问题,视觉伺服控制可以分为四大类。
- Dynamic position-based look-and-move
- Dynamic image-based look-and-move
- Direct position-based visual servo
- Direct image-based visual servo
下图展示了Dynamic position-based look-and-move的框架,如果是非分层的,则没有Joint controllers这一层,如果是image-based,则没有Pose estimation这一项。

虽然分层控制看上去多了一个处理步骤,但实际中的视觉伺服大都采用分层控制,主要有以下几个原因
- 一般来说,控制器的频率大于1KHZ是很常见的,但是图像采样频率达到1KHZ是比较难的,因此直接控制没法满足高频的控制要求。
- 对许多机器人来说,在3D空间下的姿态和位移甚至速度加速度都很容易通过自身或附加的传感器得到,而且精度较图像高。
- 对于单纯的机器人定点运动,有许多成熟的方法可以直接运用。
关于基于位置和基于图像,简单来讲,基于图像,误差就是当前特征在图像的位置和在目标图像的位置,而基于位置,则要先将图像特征转换到工作空间三维坐标系,然后计算在三维空间下当前位置和目标位置的误差。
考虑一个例子,用机器手去抓一个杯子。假设,我们的相机就在机器手上,什么意思呢?就是这个相机没法捕捉到完整的机器手,只能捕捉到目标。那这个时候怎么判断杯子是否抓稳了呢?比如说,我们以杯子的中心在视野中央当作抓稳的判断条件。这样可能会出现什么问题呢?当相机有误差时,也就是说,杯子实际上并不在机器手中央,但是由于相机的偏移或者其他误差导致杯子显示在捕捉到的图像中央。注意,这时候,无论是基于图像还是基于位置,都无法自己发现这个误差并纠正。那什么样的做法比较合理呢?对,把相机换个位置,换到能同时观察到机器手和杯子的位置,这样就算有偏移,也能知道是否抓稳。
这个例子不一定恰当,有点像控制中引入反馈的意思?我们为了区分这两种情况,将能同时观察到执行机构和目标的系统称为终点闭环(endpoint closed-loop,ECL)系统,反之,称为终点开环(endpoint open-loop,EOL)系统。理论上闭环效果更好,但是闭环意味着引入了更多的计算量(需要同时识别并追踪更多的特征),所以这也是一个trade off。
基于位置的视觉伺服控制
基于位置的视觉伺服控制,首先从图像中提取特征,然后基于这些特征估计目标相对于相机的位姿,将该位姿与预期的目标位姿进行对比,当误差为0或者小于 δ \delta δ时,认为控制任务完成。简单起见,下述讨论时我们默认采用比例控制。考虑将末端执行机构上的某个点 e P ^e \mathbf{P} eP移动到固定参考系下的另一个点 S \mathbf{S} S,称该过程为点到点(point-to-point)。我们先考虑只有平动的情况,即 T = ℜ 3 \mathcal{T} = \Re^3 T=ℜ3,如果相机是固定的话,则可以定义如下误差函数
E p p ( x e ; S , e P ) = x e ( e P ) − S \mathbf{E}_{pp}\mathbf{(x_e;S,{^eP})=x_e(^eP)-S} Epp(xe;S,eP)=xe(eP)−S当然,很多时候并不是能够轻易地获得目标的全局位置,更多是知道相对于相机的位置,因此,我们的控制律可以写为
u 3 = − k E p p ( x ^ e ; x ^ c ( c S ^ ) , e P ) = − k ( x ^ e ( e P ) − x ^ c ( c S ^ ) ) \mathbf{u}_3=-k \mathbf{E}_{pp}(\mathbf{\hat{x}}_e;\mathbf{\hat{x}}_c(^c\mathbf{\hat{S}}),{^e\mathbf{P}})=-k(\mathbf{\hat{x}}_e(^e\mathbf{P})-\mathbf{\hat{x}}_c(^c\mathbf{\hat{S}})) u3=−kEpp(x^e;x^c(cS^),eP)=−k(x^e(eP)−x^c(cS^))实际相机都需要事先进行标定,但误差不可避免,因此这里的 x ^ \mathbf{\hat{x}} x^表示对应的估计值。如果相机是固定在机器人上的某个位置,则相机相对末端执行机构的变换是已知的,有
u 3 = − k x ^ c ( c P ^ − c S ^ ) \mathbf{u}_3=-k\mathbf{\hat{x}}_c(^c\mathbf{\hat{P}}-{^c\mathbf{\hat{S}})} u3=−kx^c(cP^−cS^) e u 3 = − k e x ^ c ( c P ^ − c S ^ ) ^e\mathbf{u}_3=-k^e\mathbf{\hat{x}}_c(^c\mathbf{\hat{P}}-{^c\mathbf{\hat{S}})} eu3=−kex^c(cP^−cS^)注意,上述两个式子等于0的条件时一样的。 ( c P ^ − c S ^ ) = 0 (^c\mathbf{\hat{P}}-{^c\mathbf{\hat{S}})}=0 (cP^−cS^)=0。也就是说,这个收敛条件并不依赖于机器人执行机构的准确性或者相机标定结果。
更进一步地,考虑平动+转动的情况,即 T ⊆ S E 3 \mathcal{T} \subseteq SE^3 T⊆SE3,此时的控制输入 u ∈ ℜ 6 \mathbf{u} \in \Re^6 u∈ℜ6。但是我们上面定义的误差函数是3维的,怎么解决维数不一致的问题呢?在刚体运动那一小节中,我们得到了一个式子 P ˙ = A ( P ) r ˙ \mathbf{\dot{P}}=\mathbf{A(P)}\dot{\mathbf{r}} P˙=A(P)r˙,结合该式可以得到
P ˙ = u 3 = A ( P ) u \mathbf{\dot{P}}=\mathbf{u}_3=\mathbf{A(P)}\mathbf{u} P˙=u3=A(P)u为了得到 u \mathbf{u} u,理论上,我们只需要解上述这个方程即可,那么问题来了,如果 A ( P ) \mathbf{A(P)} A(P)是方阵当然万事大吉,但是很显然这里不是。不要慌,伟大的数学家早已经看穿了一切,这里就要引进一个重要的概念,PM广义逆,具体定义感兴趣的朋友可以去找本矩阵论看看。这里主要用到如下结论
矩阵 A ∈ C m × n A \in \mathbb{C}^{m \times n} A∈Cm×n且 r a n k ( A ) = r rank(A)=r rank(A)=r,则

上面的 A + A^+ A+就是广义逆,而且注意到 A ( P ) \mathbf{A(P)} A(P)的定义中含有一个单位阵,因此它一定是行满秩的。
那刚才的那个问题就很好解答了
u = A ( P ) + u 3 \mathbf{u}=\mathbf{A(P)}^+\mathbf{u}_3 u=A(P)+u3在刚才的基础上更进一步,假设现在不是把末端执行机构移动到某个位姿,而是把他移到某两个点的连线上。首先要重新定义一个误差函数,这个误差函数必须满足三点共线时值为0,且偏离角度越大值越大。那我们自然就会想到向量积。
E p l ( x e ; S 1 , S 2 , e P ) = ( S 2 − S 1 ) × ( x e ( e P ) − S 1 ) × ( S 2 − S 1 ) \mathbf{E}_{pl}\mathbf{(x_e;S_1,S_2,{^eP})}=(\mathbf{S}_2-\mathbf{S}_1)\times (\mathbf{x}_e(^e\mathbf{P})-\mathbf{S}_1) \times (\mathbf{S}_2-\mathbf{S}_1) Epl(xe;S1,S2,eP)=(S2−S1)×(xe(eP)−S1)×(S2−S1)我们刚才考虑的是把末端执行机构的一个点移动到一条线上,这个动作即使不考虑旋转,单纯的平动就可以做到。如果同时考虑把两个点移动到同一条线上,那么很显然,除非一开始这两条线就是平行的,否则无法通过单纯的平动实现该目标。
令 u = ( T , Ω ) \mathbf{u=(T,\Omega)} u=(T,Ω),利用向量积很容易表述两个向量之间的差异
k = ( S 2 − S 1 ) × R e ( e P 2 − P 1 ) \mathbf{k}=(\mathbf{S}_2-\mathbf{S}_1) \times \mathbf{R_e}(^e\mathbf{P}_2-\mathbf{P}_1) k=(S2−S1)×Re(eP2−P1)这里 k \mathbf{k} k的方向表示旋转轴,模长正比于夹角, R e \mathbf{R_e} Re表示旋转矩阵。此时
Ω = − k 1 k \mathbf{\Omega}=-k_1\mathbf{k} Ω=−k1k此时的平动肯定不是简单的 − k 2 E p l -k_2\mathbf{E}_{pl} −k2Epl,因为发生了旋转,结合我们在刚体运动小节介绍的结果,很容易得到
T = − k 2 ( S 2 − S 1 ) × ( x e ( e P 1 ) − S 1 ) × ( S 2 − S 1 ) − Ω × ( x e ( e P 1 ) ) \mathbf{T}=-k_2(\mathbf{S}_2-\mathbf{S}_1)\times (\mathbf{x}_e(^e\mathbf{P}_1)-\mathbf{S}_1) \times (\mathbf{S}_2-\mathbf{S}_1)-\mathbf{\Omega}\times(\mathbf{x}_e(^e\mathbf{P}_1)) T=−k2(S2−S1)×(xe(eP1)−S1)×(S2−S1)−Ω×(xe(eP1))上述讨论都是基于单相机的情况,实际上,在进行估计时,采用多传感器是很常见的减小误差的方法,下面我们简单讨论一下多相机的情况。令 a x c 1 ^a\mathbf{x}_{c1} axc1表示相机相对于任意一个参考系 a a a的位姿, a P = [ x , y , z ] T ^a\mathbf{P}=[x,y,z]^T aP=[x,y,z]T,则有
p 1 = [ u 1 v 1 ] = λ z a P + t z [ x a P + t x y a P + t y ] \mathbf{p}_1=\begin{bmatrix} u_1 \\ v_1\end{bmatrix}=\frac{\lambda}{\mathbf{z}{^a\mathbf{P}}+t_z} \begin{bmatrix} \mathbf{x}{^a\mathbf{P}}+t_x \\ \mathbf{y}{^a\mathbf{P}}+t_y\end{bmatrix} p1=[u1v1]=zaP+tzλ[xaP+txyaP+ty]其中, x , y , z \mathbf{x},\mathbf{y},\mathbf{z} x,y,z是旋转矩阵 c 1 R a ^{c1}\mathbf{R}_a c1Ra的对应行向量, t x , t y , t z t_x,t_y,t_z tx,ty,tz同理。简单化简可得
A 1 ( p 1 ) a P = b 1 ( p 1 ) A_1(\mathbf{p}_1)^a\mathbf{P}=b_1(\mathbf{p}_1) A1(p1)aP=b1(p1)其中
A 1 ( p 1 ) = [ λ x − u 1 z λ y − v 1 z ] , b 1 ( p 1 ) = [ u 1 t z − λ t x v 1 t z − λ t y ] A_1(\mathbf{p}_1)=\begin{bmatrix} \lambda \mathbf{x}-u_1 \mathbf{z} \\ \lambda \mathbf{y}-v_1 \mathbf{z}\end{bmatrix},b_1(\mathbf{p}_1)=\begin{bmatrix} u_1 \mathbf{t}_z-\lambda t_x \\ v_1 \mathbf{t}_z-\lambda t_y\end{bmatrix} A1(p1)=[λx−u1zλy−v1z],b1(p1)=[u1tz−λtxv1tz−λty]同理,对另一个相机 a x c 2 ^a\mathbf{x}_{c2} axc2我们也有如上结果,写成矩阵形式
[ A 1 ( p 1 ) A 2 ( p 2 ) ] a P = [ b 1 ( p 1 ) b 2 ( p 2 ) ] \begin{bmatrix}A_1(\mathbf{p}_1) \\ A_2(\mathbf{p}_2)\end{bmatrix}{^a\mathbf{P}}=\begin{bmatrix}b_1(\mathbf{p}_1) \\ b_2(\mathbf{p}_2)\end{bmatrix} [A1(p1)A2(p2)]aP=[b1(p1)b2(p2)]很显然,当多个相机方程联立的时候,方程个数会大于未知数个数,当然引入多个相机的目的就是为了防止某个相机的误差对结果影响过大,上述方程通过最小二乘的方法很容易得到一个解,这里不加赘述。
基于位置的视觉伺服控制的基本理论主要都介绍了,总的来说,基于位置控制的优点就是将目标从二维图像转换到三维空间,对机器手来说,从(1,2,3)到(3,4,5)显然比从图上的(1,2)到(3,4)更好理解一些。缺点的话,引进从图像到空间的变换自然也引进了新的误差,因此,基于位置的方法都对相机的标定结果比较敏感。另一个问题就是在重复计算坐标变换的过程,需要许多额外的计算量。
基于图像的视觉伺服控制
首先引入图像雅可比矩阵的概念,定义 r \mathbf{r} r和 r ˙ \mathbf{\dot{r}} r˙分别表示末端执行机构的位姿和速度, f \mathbf{f} f和 f ˙ \mathbf{\dot{f}} f˙表示图像特征的参数和这些参数的变化率。定义
f ˙ = J v ( r ) r ˙ \mathbf{\dot{f}}=\mathbf{J}_v(\mathbf{r})\mathbf{\dot{r}} f˙=Jv(r)r˙其中,
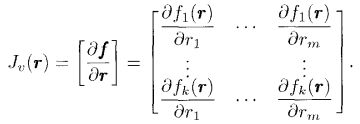
J v \mathbf{J}_v Jv称为图像雅克比矩阵。举个例子来说明如何求解图像雅可比矩阵。利用前面的运动学公式,有
P ˙ = Ω × P + T \mathbf{\dot{P}}=\Omega\times \mathbf{P}+\mathbf{T} P˙=Ω×P+T结合
[ u v ] = λ z [ x y ] \begin{bmatrix} u \\ v\end{bmatrix}=\frac{\lambda}{z} \begin{bmatrix} x \\ y\end{bmatrix} [uv]=zλ[xy]有
x ˙ = z ω y − u z λ ω z + T x \dot{x}=z\omega_y -\frac{uz}{\lambda}\omega_z +T_x x˙=zωy−λuzωz+Tx y ˙ = u z λ ω z − z ω w + T y \dot{y}=\frac{uz}{\lambda}\omega_z -z\omega_w +T_y y˙=λuzωz−zωw+Ty z ˙ = z λ ( v ω x − u ω y ) + T z \dot{z}=\frac{z}{\lambda}(v\omega_x -u\omega_y )+T_z z˙=λz(vωx−uωy)+Tz把上述结果代入
u ˙ = λ z x ˙ − x z ˙ z 2 \dot{u}=\lambda \frac{z\dot{x}-x\dot{z}}{z^2} u˙=λz2zx˙−xz˙化简得
u ˙ = λ z T x − u z T z − u v λ ω x + λ 2 + u 2 λ ω y − v ω z \dot{u}=\frac{\lambda}{z}T_x-\frac{u}{z}T_z-\frac{uv}{\lambda}\omega_x+\frac{\lambda^2+u^2}{\lambda}\omega_y-v\omega_z u˙=zλTx−zuTz−λuvωx+λλ2+u2ωy−vωz同理有
v ˙ = λ z T y − v z T z + u v λ ω y − λ 2 + v 2 λ ω x + u ω z \dot{v}=\frac{\lambda}{z}T_y-\frac{v}{z}T_z+\frac{uv}{\lambda}\omega_y-\frac{\lambda^2+v^2}{\lambda}\omega_x+u\omega_z v˙=zλTy−zvTz+λuvωy−λλ2+v2ωx+uωz写成矩阵形式
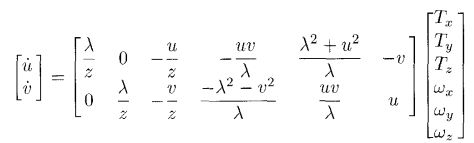
需要注意的是,雅克比矩阵是同深度 z z z相关的。
现在我们知道了雅克比矩阵,理论上只要知道 r ˙ \dot{r} r˙就能知道 f ˙ \dot{f} f˙,知道 f ˙ \dot{f} f˙就能知道 r ˙ \dot{r} r˙,那这里又回到了之前的问题,雅克比矩阵是否一定可逆?如果同时有多组特征怎么办?还是老办法,利用最小二乘和广义逆,这里给出通解
r ˙ = J v + f ˙ + ( I − J v + J v ) b \mathbf{\dot{r}}=\mathbf{J}_v^+\mathbf{\dot{f}}+(\mathbf{I}-\mathbf{J}_v^+\mathbf{J}_v)\mathbf{b} r˙=Jv+f˙+(I−Jv+Jv)b现在我们回到实践中去,基于图像的最大问题是什么呢?少了一个维度,这是很致命的,三维空间从一个点到另一个点是唯一的,但是我们都知道,相机平面上的一个点实际对应三维的一条线,举个例子
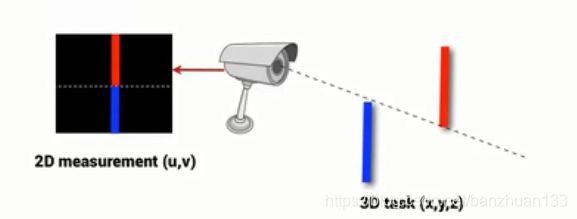
怎么解决呢?很简单,没有什么是加一个相机解决不了的,如果有
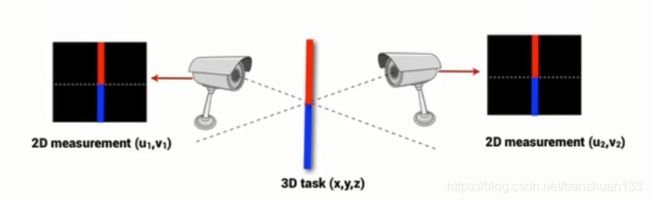
假设点 P \mathbf{P} P和 S \mathbf{S} S在左右相机平面的投影分别为 [ u l , v l ] T [u^l,v^l]^T [ul,vl]T, [ u r , v r ] T [u^r,v^r]^T [ur,vr]T, [ u s l , v s l ] T [u^l_s,v^l_s]^T [usl,vsl]T, [ u s r , v s r ] T [u^r_s,v^r_s]^T [usr,vsr]T, f = [ u l , v l , u r , v r ] T f=[u^l,v^l,u^r,v^r]^T f=[ul,vl,ur,vr]T, f d = [ u s l , v s l , u s r , v s r ] T f_d=[u^l_s,v^l_s,u^r_s,v^r_s]^T fd=[usl,vsl,usr,vsr]T,则误差函数可定义为
e p p ( f ) = f − f d \mathbf{e}_{pp}(\mathbf{f})=\mathbf{f}-\mathbf{f}_d epp(f)=f−fd同样的,上述讨论的是点对点的运动,如果基于图像来考虑点到线的运动呢?我们刚才提到点对点会出现二维一致三维不一致的情况,同样的,由于缺少深度信息,将点移动到一条线上也会出现这个问题,因此同样需要在两个或者多个平面内达到共线。回忆我们前面利用空间向量积来判断共线,类似的
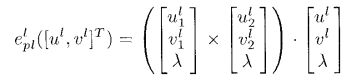
上式为0当且仅当共线的时候。
从而构造误差函数如下
e ( f ) = [ e p l l ( [ u l , v l ] T ) e p l r ( [ u r , v r ] T ) ] \mathbf{e(f)}=\begin{bmatrix} e^l_{pl}([u^l,v^l]^T) \\ e^r_{pl}([u^r,v^r]^T)\end{bmatrix} e(f)=[epll([ul,vl]T)eplr([ur,vr]T)]
我们前面也提到了,基于位置的方法很多时候对相机标定参数比较敏感,反过来讲,基于图像的优点就是不依赖于相机标定参数。因为只要误差是收敛到0的,说明在不同相机视野里都是趋近目标位置的,即使标定参数有误差也没有关系。值得注意的是,假设我们要完全控制六个自由度,那么我们至少需要选取三组特征 [ u 1 , v 1 ] , [ u 2 , v 2 ] , [ u 3 , v 3 ] [u_1,v_1],[u_2,v_2],[u_3,v_3] [u1,v1],[u2,v2],[u3,v3],对应的图像雅克比为 J v 1 , J v 2 , J v 3 \mathbf{J}_{v1},\mathbf{J}_{v2},\mathbf{J}_{v3} Jv1,Jv2,Jv3,记 J v = [ J v 1 , J v 2 , J v 3 ] T \mathbf{J}_{v}=[\mathbf{J}_{v1},\mathbf{J}_{v2},\mathbf{J}_{v3}]^T Jv=[Jv1,Jv2,Jv3]T,那么可能会出现该矩阵为奇异的情况,因此,更多情况下,选取图像特征的维数都大于所要控制的自由度。
关于图像雅可比矩阵,我们上述解方程默认都是已知的,但是前面也提到了,雅可比矩阵需要知道深度,那么最理想的情况当然每个时刻都能获取到深度信息。假设,为了减少计算量,只选择若干个点,事先计算好对应相机的雅可比矩阵,那么应该怎么选取?其中一种常见的方法是选取 e = 0 \mathbf{e=0} e=0的位置。1
参考文献
- Seth Hutchinson, “A Tutorial on Visual Servo Control,” IEEE TRANSACTIONS O N ROROTLCS AND AUTOMATION, VOL. 12, NO. 5 , OCTOBER 1996
- Seth Hutchinson,“Visual Servo Control Part I: Basic Approaches”,IEEE Robotics & Automation Magazine,DECEMBER 2006
B. Espiau, F. Chaumette, and P. Rives, “A new approach to visual servoing in robotics,” IEEE Trans. Robotics and Automation, vol. 8, pp.313–326, June 1992 ↩︎