算法刷题系列--leetcode -题#160#404#437
近期刷题
- leetcode-437-路径总和 III
- leetcode-404-左叶子之和
- leetcode-160-相交链表
leetcode-437-路径总和 III
题目描述:
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
解题思路
首先看到这道题我们得知道是一道要对二叉树遍历的题,二叉树遍历?你得要跟条件反射一样想到二叉树递归遍历的模板!二叉树递归遍历模板几乎长一个样,给个前序遍历意思一下:
void traverse(root) {
if (root == null) return;
traverse(root.left);
traverse(root.right);
}
关于递归其实有个很玄的现象,就是如果对于一个递归,你要深入的深究它执行的每一步,但这种情况往往会把人绕晕,我认为我们老老实实实的写好一下两样递归的要素就行,其他交给递归去处理:
- 中止调用的条件
- 递归主体
这道题中,利用两个递归,咋一看很复杂,其实两个递归是各司其职,界限分明。
- 一个递归求从任意一个节点开始有多少条满足条件的路径。
- 一个递归是遍历整棵树,求各个节点开始各有多少满足条件的路径数,各路径数相加即可得出符合条件的总路径数
代码
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {number} sum
* @return {number}
*/
var pathSum = function(root, sum) { //root为根节点, sum为规定的路径权值和
if(!root) return 0 //若节点为空,返回0
let page = findDown(root,sum) //从根节点开始有多少满足条件的路径数,findDown函数是求从单个节点开始满足条件的路径数
let sum1 = pathSum(root.left, sum) //遍历左子树求符合条件的路径数,
let sum2 = pathSum(root.right, sum) //遍历右子树求符合条件的路径数
return page + sum1 +sum2; //得出总路径数
};
function findDown(tNode, sum) { // 求从单个节点开始满足条件的路径数,tNode为当前节点,sum为规定的路径权值和
if(!tNode) return 0 //若节点为空,返回0
let flag = tNode.val === sum ? 1 : 0 // 当前节点权值刚好等于sum则算为1,否则为0
let leftSum = findDown(tNode.left, sum - tNode.val) //剩下的权值要子树来凑,先看左子树能不能凑出来
let rightSum = findDown(tNode.right, sum-tNode.val) //再看右子树是否能凑出来
return flag + leftSum + rightSum // 返回符合条件的路径数
}
leetcode-404-相交链表左叶子之和
题目描述:
计算给定二叉树的所有左叶子之和。
示例:
3
/ \
9 20
/ \
15 7
在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
解题思路
看是不是需要遍历二叉树,要的话直接上递归遍历模板,再补充细节。。。
实现的思路就是
确定边界点:当前节点不存在时,返回0
当存在左子树时:
判断左节点是否为叶子节点,是的话返回该左节点的值 加上递归右子树的值,若不是叶子节点,证明还有左子树或者右子树,就递归左右子树即可
当左子树不存在时,直接递归遍历右子树即可
代码
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var sumOfLeftLeaves = function(root) {
if(!root) return 0; //根节点为空,则返回0
if(root.left) { //若左子树存在,则有存在左叶子的可能
if(isLeaf(root.left)) { //左节点是否为叶子节点
return root.left.val + sumOfLeftLeaves(root.right) //为叶子节点则加上该左节点的权值 及遍历右子树得出的权值
}else { 若不是叶子节点,说明还需继续往下遍历找出该左子树下的所有左叶子
return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right)
}
} else { //若左子树不存在,那直接递归遍历右子树得了
return sumOfLeftLeaves(root.right)
}
};
function isLeaf(node) { //判断当前节点是否为叶子节点
if(!node) return false
if(!node.left && !node.right) return true
}
leetcode-160-相交链表
题目描述:
编写一个程序,找到两个单链表相交的起始节点。如下面的两个链表:

在节点 c1 开始相交。
示例:
输入:
intersectVal = 8,listA = [4,1,8,4,5],listB = [5,0,1,84,5],skipA = 2,
skipB = 3
输出:
Reference of the node with value = 8
输入解释:
相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
注意:
如果两个链表没有交点,返回 null.
在返回结果后,两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
解题思路
这道题我们要明确一件事,就是如果两链表如果交叉了,那交叉部分的任一节点指针都是指向同一块内存,理所当然的,我们只需要找出第一个相等的节点即可,因为有相等节点说明交叉了
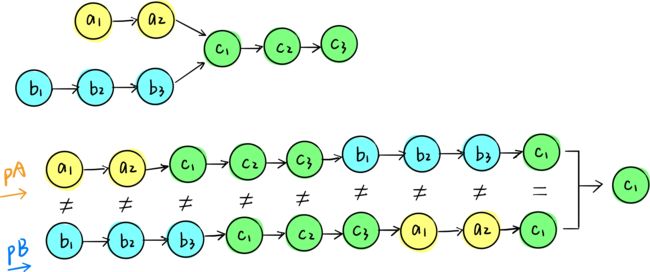
采用题目中第一幅图:

本题采用双指针法解答较为清楚明了,若我们把两链表从图到尾连起来
分别是链表A及链表B,现在我们以链表A开头,拼上链表B则为:
a1->a2->c1->c2->c3->b1->b2->b3->c1->c2->c3
同理,我把链表B放在开头,A拼在后面,则拼接后链表为:
b1->b2->b3->c1->c2->c3->a1->a2->c1->c2->c3
大家看到没有,这两条链表的长度必然是一样的,而且有相交的肯定是靠后位置(如果比较早开始相交或者也在前面)
这样子我们就可以从头开始对比了,只要一遇到对应位置相等的节点,可断定这两链表相交。
对比链表过程也是遍历过程,编列两个链表最常用的是定义两个指针以记录遍历位置。另外,也无需真的把链表拼接在一起再比较,只需要一边遍历完,该指针指向另一链表头结点即可。如
A链表头指针headA, B链表头指针为headB,设A记录指针为PA, B记录指针为PB, PA遍历完A, 立马使PA = headB,PB也是类似如此,来看下代码
代码
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} headA
* @param {ListNode} headB
* @return {ListNode}
*/
var getIntersectionNode = function(headA, headB) {
let PA = headA
let PB = headB
while(PA !== PB) {
PA = PA ? PA.next : headB // PA遍历完A链表, 立马使PA = headB
PB = PB ? PB.next : headA // PB遍历完A链表, 立马使PB = headA
}
return PA
};
最后,推荐一个图
参考地址
JavaScript相交链表 图解双指针法