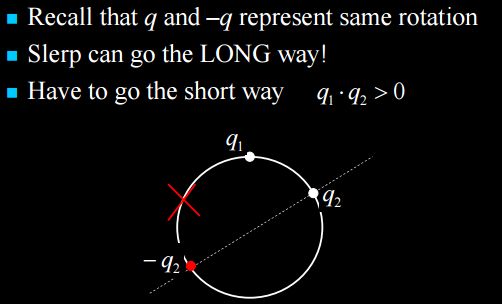基于单位四元数的姿态插补（Matlab）

写在前面

Matlab机器人工具箱版本9.10

在我前面的博文基于抛物线过渡（梯形加减速）的空间直线插补算法与空间圆弧插补算法、五自由度diy机械臂空间插补算法(直线和圆弧)简单测试中出现姿态奇异性问题，这主要是由于我选用的RPY角姿态表达方法在β角等于±90°时姿态解算会出现奇异现象，剩下两个自由度会退化，α角和γ角会变成一个角。为解决这个问题，我换用单位四元数来对姿态进行表达。

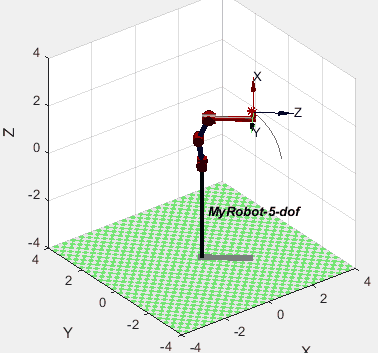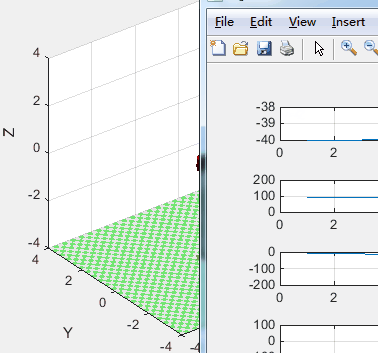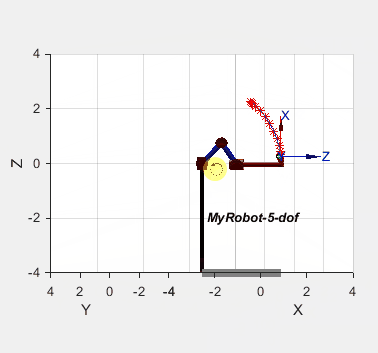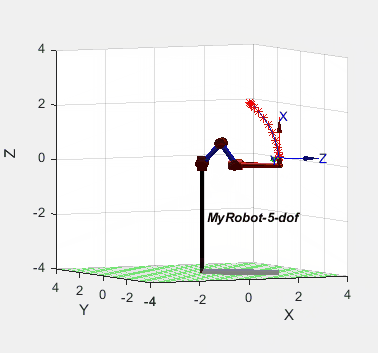
结果显示能够解决奇异性问题：

机器人姿态表达

机器人姿态表达形式主要有旋转矩阵法、欧拉角法、RPY角法、单位四元数法等。

旋转矩阵法可以通过累乘表示坐标系的连续变化，能够清晰地表示当前坐标系相对于基座标系的姿态，是常用的姿态表达方式。但是由于旋转矩阵法需要9个元素才能描述姿态，在程序处理中需要使用大量内存空间且计算复杂，所以旋转矩阵法不适合应用与实时性较高的姿态控制和运动插补控制中。

欧拉角法和RPY角法都能非常简单地描述物体姿态。机器人末端执行器的示教姿态通常以欧拉角的形式给出，RPY通常表示船舶在航行中的姿态变化，都存在奇异性问题。

单位四元数在表达姿态时具有运算量小、便于插值等优势，而且单位四元数插补得到的中间姿态要比欧拉角法表示刚体旋转更为自然，同样的姿态变换下，欧拉角的姿态变化幅度大，因此单位四元数法要比欧拉法更加适合描述刚体姿态的变换。

预备知识

关于四元数的定义以及基本知识，阅读下面著作即可：

常用的四元数知识：

• 四元数的求负是对每个分量变负就可以了，即$\mathbf{q}=(w,x,y,z),-\mathbf{q}=(-w,-x,-y,-z)$ 。但是q和-q表示的角位移是相同的，当旋转角为360°或其整数倍时，不会改变q的角位移，但是q的四个分量都变负了
• 四元数与标量相乘：$k\mathbf{q}=k[w,x,y,z]=[kw,kx,ky,kz]$
• 四元数的点乘:${\mathbf{q}}_1\cdot {\mathbf{q}}_2=\left[w_1{\mathbf{v}}_1\right]\cdot \left[w_2{\mathbf{v}}_2\right]=w_1{w}_2+{\mathbf{v}}_1\cdot {\mathbf{v}}_2=w_1{w}_2+x_1{x}_2+y_1{y}_2+z_1{z}_2$。四元数点乘的绝对值越大，代表其方向越相近
• 四元数乘法（叉乘）：$\mathbf{p}=t+v,\mathbf{q}=a+u$，则$\mathbf{p}\mathbf{q}=at-u\cdot v+av+tu+u\times v$
• 四元数的模长（范数）：$\Vert \mathbf{q}\Vert =\sqrt{x^2+y^2+z^2+w^2}=\sqrt{\mathbf{q}\cdot {\mathbf{q}}^{\ast }}$ 。若$\Vert \mathbf{q}\Vert =1$，这样的四元数称为单位四元数
• 四元数的共轭：四元数的共轭就是让四元数的向量部分取负，即若$\mathbf{q}=(w,x,y,z)$ ，则其共轭为${\mathbf{q}}^{\ast }=(w,-x,-y,-z)$
• 四元数的逆：由于$\mathbf{q}{\mathbf{q}}^{\ast }=\Vert \mathbf{q}{\Vert }^2$ ，因此$\mathbf{q}\frac{{\mathbf{q}}^{\ast }}{\Vert \mathbf{q}{\Vert }^2}=1$ 。若四元数存在逆${\mathbf{q}}^{-1}$ ，则$\mathbf{q}{\mathbf{q}}^{-1}={\mathbf{q}}^{-1}\mathbf{q}=1$，因此当$\Vert \mathbf{q}\Vert \ne 0$ 时：

$${\mathbf{q}}^{-1}=\frac{{\mathbf{q}}^{\ast }}{\Vert \mathbf{q}{\Vert }^2}（1）$$

​ 对于单元四元数来说，${\mathbf{q}}^{-1}={\mathbf{q}}^{\ast }$

• 用四元数旋转矢量：对于矢量$v=(x,y,z)$，给定一个单位四元数q，让$v$旋转q。首先将$v$改写成四元素的形式 $\mathbf{v}$= (0, x, y ,z)，接下来进行如下变换：

$${\mathbf{v}}^{\prime }=\mathbf{q}\mathbf{v}{\mathbf{q}}^{-1}（2）$$

• 刚体旋转的欧拉定理表明，刚体的任意次旋转都可以简化为刚体绕着固定轴的一次旋转。四元数向旋转矩阵转换公式为：

$$R=\left[\begin{array}{ccc}{q}_0^2+q_1^2-q_2^2-q_3^2& 2\left(q_1{q}_2-q_0{q}_3\right)& 2\left(q_1{q}_3+q_0{q}_2\right)\\ 2\left(q_1{q}_2+q_0{q}_3\right)& q_0^2-q_1^2+q_2^2-q_3^2& 2\left(q_2{q}_3-q_0{q}_1\right)\\ 2\left(q_1{q}_3-q_0{q}_2\right)& 2\left(q_2{q}_3+q_0{q}_1\right)& q_0^2-q_1^2-q_2^2+q_3^2\end{array}\right]（3）$$

​ 同时机械臂末端姿态矩阵R为：
$$\mathbf{R}=\left[\begin{array}{lll}{n}_x& o_x& a_x\\ n_y& o_y& a_y\\ n_z& o_z& a_z\end{array}\right]（4）$$
​ 解得对应的四元数为：
$$q=q_1+q_{2}i+q_{3}j+q_{4}k（5）$$
​ 其中，$q_1=\frac{1}{2}\sqrt{n_x+o_y+a_z+1}$，虽然开方有负数，考虑$\theta \in [-\pi /2,\pi /2]$，故$q_1=cos\theta >0$，其余元素的正负号由下式决定：
$$\{\begin{array}{l}4as=o_z-a_y\\ 4bs=a_x-n_z\\ 4cs=n_y-o_x\end{array}（6）$$
​ 故得到各元素为:
$$q_1=\frac{1}{2}\sqrt{n_x+o_y+a_z+1}（7）$$

$$q_2=\frac{1}{2}\mathrm{sign}\left(o_z-a_y\right)\sqrt{n_x-o_y-a_z+1}（8）$$

$$q_3=\frac{1}{2}\mathrm{sign}\left(a_x-n_z\right)\sqrt{-n_x+o_y-a_z+1}（9）$$

$$q_4=\frac{1}{2}\mathrm{sign}\left(n_y-o_x\right)\sqrt{-n_x-o_y+a_z+1}（10）$$

单位四元数球面线性插值

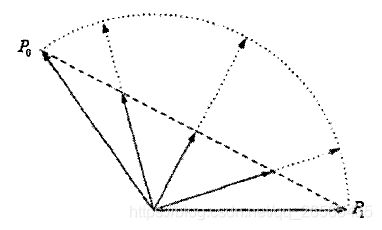
对于一般的线性插值来说：$r=p_0+\left(p_1-p_0\right)t$，其中$t\in [0,1]$，代表了插值矢量r末端在弦$P_0-P_1$上的位置。如下图所示，假设的取值为1/4、2/4、3/4，也就是将P0P1弦长均分为4等份，可以看出其对应的弧长并不相等。靠近中间位置的弧长较长，而靠近两段处的弧长较短，这就意味着当t匀速变化时，代表姿态矢量的角速度变化并不均匀。

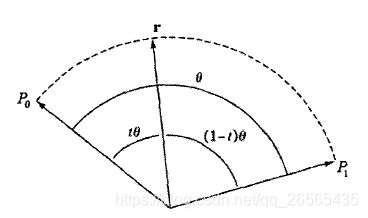
为了更好的解决非恒定旋转速度和归一化问题，需要一种球面线性插值SLERP。SLERP类似于线性插值，除了不是沿着一条直线插入而是沿着球体表面上的一个弧进行插值，如下图所示。

下面来推导一下SLERP公式。插值的一般公式可以写为：
$$r=a(t)P_0+b(t)P_1（11）$$
现在要找到合适的$a(t)$和$b(t)$。注意单位向量$P_0$和$P_1$之间的夹角为$\theta$，$P_0$和r之间的夹角为$t\theta$，$P_1$和r之间的夹角为$(1-t)\theta$：

将（11）两边同乘$P_0$可得
$$P_0\cdot r=a(t)P_0\cdot P_0+b(t)P_0\cdot P_1（12）$$

$$\cos t\theta =a(t)+b(t)\cos \theta （13）$$

同样对（11）两边同乘$P_1$可得
$$\cos [(1-t)\theta ]=a(t)\cos \theta +b(t)（14）$$
两个方程可以解出两个未知量$a(t)$和$b(t)$：
$$a(t)=\frac{\cos t\theta -\cos [(1-t)\theta ]\cos \theta }{1-{\cos }^2\theta }（15）$$

$$b(t)=\frac{\cos [(1-t)\theta ]-\cos t\theta \cos \theta }{1-{\cos }^2\theta }（16）$$

简化后可得单位四元数的球面线性插值表达式为：
$$\mathrm{Slerp}\left(P_0,P_1,t\right)=\frac{\sin [(1-t)\theta ]}{\sin \theta }{P}_0+\frac{\sin [t\theta ]}{\sin \theta }{P}_1（17）$$
注意这个公式有2个问题，必须在实现过程中加以考虑：

• 如果四元数点积的结果是负值（夹角大于90°），那么后面的插值就会在4D球面上绕远路。为了解决这个问题，先测试点积的结果，当结果是负值时，将2个四元数的其中一个取反（并不会改变它代表的朝向）。而经过这一步操作，可以保证这个旋转走的是最短路径。

• 当p和q的夹角θ差非常小时会导致sinθ→0，这时除法可能会出现问题。为了避免这样的问题，当θ非常小时可以使用简单的线性插值代替（θ→0时，sinθ≈θ，因此方程退化为线性方程：slerp(p,q,t)=(1-t)p+tq

替换掉前面博文代码中的RPY姿态插补部分，修改一下函数参数，替换代码如下：

直线插补：

.....
% 计算两个四元数之间的夹角
dot_q = Qs.s*Qd.s + Qs.v(1)*Qd.v(1) + Qs.v(2)*Qd.v(2) + Qs.v(3)*Qd.v(3);
if (dot_q < 0)
    dot_q = -dot_q;
end
 
for i = 1: N
    % 位置插补
    x(i) = x1 + delta_x*lambda(i);
    y(i) = y1 + delta_y*lambda(i);
    z(i) = z1 + delta_z*lambda(i);
    % 单位四元数球面线性姿态插补
    % 插值点四元数
    if (dot_q > 0.9995)
        k0 = 1-lambda(i);
        k1 = lambda(i);
    else
        sin_t = sqrt(1 - power(dot_q, 2));
        omega = atan2(sin_t, dot_q);
        k0 = sin((1-lambda(i)*omega)) / sin(omega);
        k1 = sin(lambda(i)*omega) / sin(omega);
    end
    qk(i) = Qs * k0 + Qd * k1;
end

空间圆弧插补：

......
% 计算两个四元数之间的夹角
dot_q = Qs_.s*Qd_.s + Qs_.v(1)*Qd_.v(1) + Qs_.v(2)*Qd_.v(2) + Qs_.v(3)*Qd_.v(3);
if (dot_q < 0)
    dot_q = -dot_q;
end

for i = 1: N
    % 位置插补
    x_(i) = flag * r * cos(lambda(i)*delta_ang);
    y_(i) = flag * r * sin(lambda(i)*delta_ang);
    P = T*[x_(i); y_(i); 0; 1];
    x(i) = P(1);
    y(i) = P(2);
    z(i) = P(3);
    % 单位四元数球面线性姿态插补
    % 插值点四元数
    if (dot_q > 0.9995)
        k0 = 1-lambda(i);
        k1 = lambda(i);
    else
        sin_t = sqrt(1 - power(dot_q, 2));
        omega = atan2(sin_t, dot_q);
        k0 = sin((1-lambda(i))*omega) / sin(omega);
        k1 = sin(lambda(i)*omega) / sin(omega);
    end
    qk(i) = Qs_ * k0 + Qd_ * k1;
end

参考文献

四元数插值与均值（姿态平滑）

四元数法及其应用

---

2019.11.25
发现了一处错误，计算k0的程序出错了，已改成k0 = sin((1-lambda(i))*omega) / sin(omega);