生成对抗网络（GAN）

GAN 是生成模型的一种，生成模型就是用机器学习去生成我们想要的数据。正规的说法是，获取训练样本（真实数据）并训练一个模型（生成器G），该模型能按照我们定义的目标数据分布去生成数据。

1 基本思想

GAN 的核心思想源于博弈论的纳什均衡。

设定参与游戏的双方分别为一个生成器(Generator)和一个判别器(Discriminator), 生成器捕捉真实数据样本的潜在分布, 并生成新的数据样本; 判别器是一个二分类器, 判别输入是真实数据还是生成的样本。为了取得游戏胜利, 这两个游戏参与者需要不断优化, 各自提高自己的生成能力和判别能力, 这个学习优化过程就是寻找二者之间的一个纳什均衡。

GAN的计算流程与结构

GAN的计算流程与结构如下图所示：

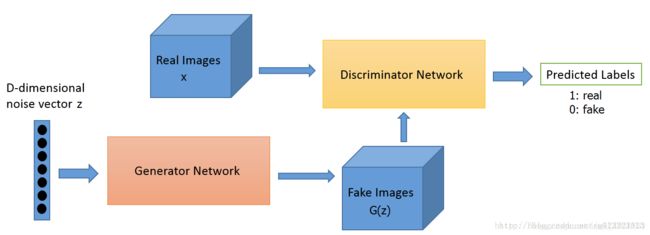
其中的生成器和判别器可以用任意可微分的函数, 这里我们用可微分函数D 和G 来分别表示判别器和生成器, 它们的输入分别为真实数据x 和随机变量z。
G(z) 为由G 生成的尽量服从真实数据分布pdata的样本。
如果判别器的输入来自真实数据, 标注为1.如果输入样本为G(z), 标注为0。
这里D 的目标是实现对数据来源的二分类判别: 真(来源于真实数据x 的分布) 或者伪(来源于生成器的伪数据G(z))。而G 的目标是使自己生成的伪数据G(z) 在D 上的表现D(G(z)) 和真实数据x 在D 上的表现D(x)一致

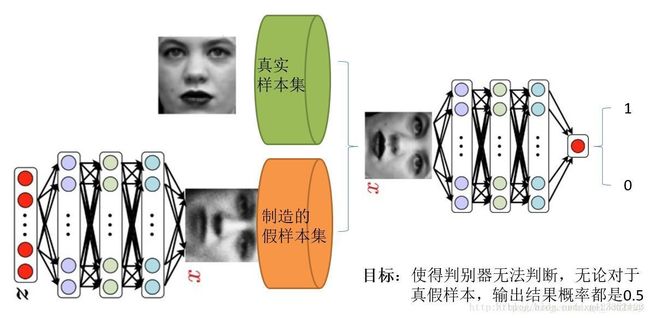
在这个人脸识别例子中：生成器和判别器都采用神经网络，我们有的只是真实采集而来的人脸样本数据集，值得一提的是我们连人脸数据集的类标签都没有，也就是我们不知道那个人脸对应的是谁，属于非监督分类。

最原始的GAN目的是想通过输入一个噪声，模拟得到一个人脸图像，这个图像可以非常逼真以至于以假乱真。(不同的任务想得到的东西不一样)

上图右半部分的判别模型，是一个简单的神经网络结构，输入一幅图像，输出是一个概率值，用于判断真假使用（概率值大于0.5那就是真，小于0.5那就是假，人们定义的概率）
左半部分的生成模型也是神经网络结构，输入是一组随机数Z，输出是一个图像，不再是一个数值。

从图中可以看到，会存在两个数据集，一个是真实数据集，另一个是假的数据集，由生成网络生成的数据集。

判别模型的目的：能判别出来属于的一张图它是来自真实样本集还是假样本集。假如输入的是真样本，网络输出就接近1，输入的是假样本，网络输出接近0。
生成网络的目的：使得自己生成样本的能力尽可能强，强到判别网络没法判断自己生成的样本是真还是假。

由此可见，生成模型与判别模型的目的正好相反，一个说我能判别得好，一个说我让你判别不好，所以叫做对抗，叫做博弈。

而最后的结果到底是谁赢，就要归结于模型设计者希望谁赢了。作为设计者的我们，如果是要得到以假乱真的样本，那么就希望生成模型赢，希望生成的样本很真，判别模型能力不足以区分真假样本。

2 训练过程

在噪声数据分布中随机采样，输入生成模型，得到一组假数据，记为D(z)；
在真实数据分布中随机采样，作为真实数据，记做x；
将前两步中某一步产生的数据作为判别网络的输入（因此判别模型的输入为两类数据，真/假），判别网络的输出值为该输入属于真实数据的概率，real为1，fake为0.
然后根据得到的概率值计算损失函数；
根据判别模型和生成模型的损失函数，可以利用反向传播算法，更新模型的参数。（先更新判别模型的参数，然后通过再采样得到的噪声数据更新生成器的参数）

生成模型与对抗模型是完全独立的两个模型，他们之间没有什么联系。那么训练采用的大原则是单独交替迭代训练。
因为是2个网络，不方便一起训练，所以才交替迭代训练。
先是判别网络：
假设现在有了生成网络（当然可能不是最好的），那么给一堆随机数组，就会得到一堆假的样本集（因为不是最终的生成模型，现在生成网络可能处于劣势，导致生成的样本不太好，很容易就被判别网络判别为假）。

现在有了这个假样本集(真样本集一直都有)，我们再人为地定义真假样本集的标签，很明显，这里我们默认真样本集的类标签为1，而假样本集的类标签为0，因为我们希望真样本集的输出尽可能为1，假样本集为0。

现在有了真样本集以及它们的label(都是1)、假样本集以及它们的label(都是0)。这样一来，单就判别网络来说，问题变成了有监督的二分类问题了，直接送进神经网络中训练就好。

判别网络训练完了。
继续来看生成网络：

对于生成网络，我们的目的是生成尽可能逼真的样本。

而原始的生成网络生成的样本的真实程度只能通过判别网络才知道，所以在训练生成网络时，需要联合判别网络才能达到训练的目的。

所以生成网络的训练其实是对生成-判别网络串接的训练，像上图显示的那样。因为如果只使用生成网络，那么无法得到误差，也就无法训练。

当通过原始的噪声数组Z生成了假样本后，把这些假样本的标签都设置为1，即认为这些假样本在生成网络训练的时候是真样本。因为此时是通过判别器来生成误差的，而误差回传的目的是使得生成器生成的假样本逐渐逼近为真样本(当假样本不真实，标签却为1时，判别器给出的误差会很大，这就迫使生成器进行很大的调整；反之，当假样本足够真实，标签为1时，判别器给出的误差就会减小，这就完成了假样本向真样本逐渐逼近的过程)，起到迷惑判别器的目的。

现在对于生成网络的训练，有了样本集（只有假样本集，没有真样本集），有了对应的label（全为1），有了误差，就可以开始训练了。

在训练这个串接网络时，一个很重要的操作是固定判别网络的参数，不让判别网络参数更新，只是让判别网络将误差传到生成网络，更新生成网络的参数。
在生成网络训练完后，可以根据用新的生成网络对先前的噪声Z生成新的假样本了，不出意外，这次生成的假样本会更真实。

有了新的真假样本集（其实是新的假样本集），就又可以重复上述过程了。

整个过程就叫单独交替训练。可以定义一个迭代次数，交替迭代到一定次数后停止即可。不出意外，这时噪声Z生成的假样本就会很真实了。
GAN设计的巧妙处之一，在于假样本在训练过程中的真假变换，这也是博弈得以进行的关键之处。

3 目标函数

上面提到，我们想要将一个随机高斯噪声z通过一个生成网络G得到一个和真的数据分布Pdata(x)差不多的生成分布PG(x;θ),其中的参数θ是网络的参数决定的，我们希望找到 θ 使得 PG(x;θ)和 Pdata(x)尽可能接近。

补充：什么是KL散度（又叫相对相对熵）：KL距离，是两个随机分布间距离的度量。

损失函数解析

max的目的是最大化D的区分度
min是最小化G和real数据集的数据分布
判别模型：D1(X)判断真实数据x为1，D2(G(Z))判断生成数据G(z)为0，那判别模型将接近最小0；但是如果判别模型不好，D1(X)判断真实数据x为0，D2(G(Z))判断生成数据G(z)为1，负的判别模型的损失函数将是一个很大的数值。
生成模型：D2(G(Z))判断生成数据G(z)为1，那判别模型将接近最小0，如果D2(G(Z))为接近0，损失函数将是一个很大的数值

GAN的生成模型最后可以通过噪声生成一个完整的真实数据（比如人脸），说明生成模型掌握了从随机噪声到人脸数据的分布规律。GAN一开始并不知道这个规律是什么样，也就是说GAN是通过一次次训练后学习到的真实样本集的数据分布。

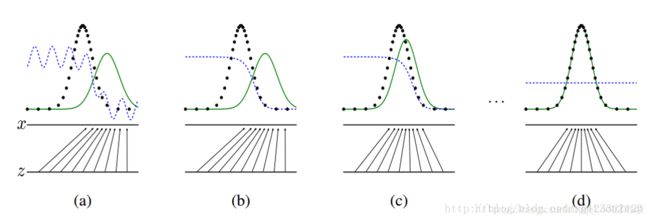
上图表明的是GAN的生成网络如何一步步从均匀分布学习到正太分布的。

黑色的点状线代表真实的数据分布，绿色的线代表生成模型G模拟的分布，蓝色的线代表判别模型D。

a图表示初始状态
b图表示，保持G不动，优化D，直到判别模型的准确率最高
c图表示保持D不动，优化G，直到混淆程度最高
d图表示，多次迭代后，终于使得G生成的数据分布能够完全与真实的数据分布一致，而D再也鉴别不出是原始数据还是由生成模型所产生的数据，从而认为G就是真实的。
GAN的另一个强大之处在于可以自动定义潜在损失函数，即判别网络可以自动学习到一个好的判别方法(损失函数)，来比较好或者不好的判别出来结果。
虽然大的loss函数是模型设计者人为定义的，基本上对于多数GAN都这么定义就可以了，但是判别网络潜在学习到的损失函数隐藏在网络之中，不同的问题这个函数就不一样，所以说可以自动学习这个潜在的损失函数。

5 优点 vs. 缺点（还需加这部分的理解与实验）

优点：

模型只用到了反向传播,而不需要马尔科夫链

训练时不需要对隐变量做推断

理论上,只要是可微分函数都可以用于构建D和G,因为能够与深度神经网络结合做深度生成式模型

G的参数更新不是直接来自数据样本,而是使用来自D的反向传播(这也是与传统方法相比差别较大的)

从实际结果来看,GAN看起来能产生更好的生成样本

GAN框架可以训练任何一种生成器网络(理论上，然而在实践中,很难使用增强学习去训练有离散输出的生成器),大多数其他架构需要生成器有一些特定的函数形式,就像输出层必须是高斯化的.另外所有其他框架需要生成器整个都是非零权值(put non-zero mass everywhere),然而,GANs可以学习到一个只在靠近真实数据的地方(神经网络层)产生样本点的模型( GANs can learn models that generate points only on a thin manifold that goes near the data.)【指的是GAN学习到的分布十分接近真实分布，这里把分布密度函数看作高维流行当中的点，某个类型的真实分布，可能是这个高维空间中的低维流行，想象三维空间中一张卷曲的纸。GAN学习的G能够尽量的“收敛”到这张纸上，而别的生成模型不行，总是在真实的流行之外有一定的分布，不够收敛。非零的mass指的是分布的“密度”，或者分布的“微元”】

没有必要遵循任何种类的因式分解去设计模型,所有的生成器和判别器都可以正常工作

相比PixelRNN, GAN生成采样的运行时间更短,GANs一次产生一个样本,然而PixelRNNs需要一个像素一个像素的去产生样本

相比VAE, GANs没有变分下界,如果鉴别器训练良好,那么生成器可以完美的学习到训练样本的分布.换句话说,GANs是渐进一致的,但是VAE是有偏差的

相比深度玻尔兹曼机, GANs没有变分下界,也没有棘手的配分函数,样本是一次生成的,而不是重复的应用马尔科夫链来生成的

相比GSNs, GANs产生的样本是一次生成的,而不是重复的应用马尔科夫链来生成的

相比NICE和Real NVE,GANs没有对潜在变量(生成器的输入值)的大小进行限制

GANs是一种以半监督方式训练分类器的方法.在你没有很多带标签的训练集的时候,你可以不做任何修改的直接使用我们的代码,通常这是因为你没有太多标记样本

GANs可以比完全明显的信念网络(NADE,PixelRNN,WaveNet等)更快的产生样本,因为它不需要在采样序列生成不同的数据

GANs不需要蒙特卡洛估计来训练网络,人们经常抱怨GANs训练不稳定,很难训练,但是他们比训练依赖于蒙特卡洛估计和对数配分函数的玻尔兹曼机简单多了.因为蒙特卡洛方法在高维空间中效果不好,玻尔兹曼机从来没有拓展到像ImgeNet任务中.GANs起码在ImageNet上训练后可以学习去画一些以假乱真的狗

相比于变分自编码器, GANs没有引入任何决定性偏置( deterministic bias),变分方法引入决定性偏置,因为他们优化对数似然的下界,而不是似然度本身,这看起来导致了VAEs生成的实例比GANs更模糊

相比非线性ICA(NICE, Real NVE等,),GANs不要求生成器输入的潜在变量有任何特定的维度或者要求生成器是可逆的

相比玻尔兹曼机和GSNs,GANs生成实例的过程只需要模型运行一次,而不是以马尔科夫链的形式迭代很多次

缺点：

可解释性差,生成模型的分布 Pg(G)没有显式的表达

比较难训练,D与G之间需要很好的同步(例如D更新k次而G更新一次)，GAN模型被定义为极小极大问题，没有损失函数，在训练过程中很难区分是否正在取得进展。GAN的学习过程可能发生崩溃问题（collapse problem），生成器开始退化，总是生成同样的样本点，无法继续学习。当生成模型崩溃时，判别模型也会对相似的样本点指向相似的方向，训练无法继续。

网络难以收敛，目前所有的理论都认为GAN应该在纳什均衡上有很好的表现，但梯度下降只有在凸函数的情况下才能保证实现纳什均衡。

训练GAN需要达到纳什均衡,有时候可以用梯度下降法做到,有时候做不到.还没有找到很好的达到纳什均衡的方法,所以训练GAN相比VAE或者PixelRNN是不稳定的,但在实践中它还是比训练玻尔兹曼机稳定的多

它很难去学习生成离散的数据,就像文本

相比玻尔兹曼机,GANs很难根据一个像素值去猜测另外一个像素值,GANs天生就是做一件事的,那就是一次产生所有像素, 你可以用BiGAN来修正这个特性,它能让你像使用玻尔兹曼机一样去使用Gibbs采样来猜测缺失值

代码分析

1、2、是我们设计的一维数据分布
3、是我们定义得全连接层
4、5、定义的生成器和判别器网络
6、网络得优化器
7、_create_model(self)定义了一个网络框架
8、def train(self) 模型得训练
9、_samples让训练好的模型网络去拟合真实数据并展示

import argparse
import numpy as np
from scipy.stats import norm
import tensorflow as tf
import matplotlib.pyplot as plt
from matplotlib import animation
import seaborn as sns

sns.set(color_codes=True)  

seed = 42#随机数的种子
np.random.seed(seed)
tf.set_random_seed(seed)

#1、真实数据高斯分布的均值和方差
class DataDistribution(object):
    def __init__(self):
        self.mu = 4
        self.sigma = 0.5


    def sample(self, N):
        samples = np.random.normal(self.mu, self.sigma, N)
        samples.sort()
        return samples

#2、随机初始化一种分布噪声点
class GeneratorDistribution(object):
    def __init__(self, range):
        self.range = range

    def sample(self, N):
        return np.linspace(-self.range, self.range, N) + \
            np.random.random(N) * 0.01

#3、随机生成权重和常数b，输出全连接层           
def linear(input, output_dim, scope=None, stddev=1.0):
    norm = tf.random_normal_initializer(stddev=stddev)
    const = tf.constant_initializer(0.0)
    with tf.variable_scope(scope or 'linear'):
        w = tf.get_variable('w', [input.get_shape()[1], output_dim], initializer=norm)
        b = tf.get_variable('b', [output_dim], initializer=const)
        return tf.matmul(input, w) + b

#4、定义生成器G，只有两层h0,h1。计算激活函数softplus，即log( exp( features ) + 1)      
def generator(input, h_dim):
    h0 = tf.nn.softplus(linear(input, h_dim, 'g0'))
    h1 = linear(h0, 1, 'g1')
    return h1

##5、定义判别器，有四层。前三层激活函数为tf.tanh，最后一层tf.sigmoid
def discriminator(input, h_dim):
    h0 = tf.tanh(linear(input, h_dim * 2, 'd0'))
    h1 = tf.tanh(linear(h0, h_dim * 2, 'd1'))   
    h2 = tf.tanh(linear(h1, h_dim * 2, scope='d2'))

    h3 = tf.sigmoid(linear(h2, 1, scope='d3'))
    return h3

#6、定义优化器，学习率衰减策略，采用梯度下降优化损失函数
#通过tf.train.exponential_decay函数实现指数衰减学习率， decay_rate为衰减系数；decay_steps为衰减速度。
#如果staircase=True，那就表明每decay_steps次计算学习速率变化，更新原始学习速率，如果是False，
#那就是每一步都更新学习速率。红色表示False，绿色表示True。  
def optimizer(loss, var_list, initial_learning_rate):
    decay = 0.95#衰减系数
    num_decay_steps = 150#150学习率更新一次
    batch = tf.Variable(0)#global_steps
    learning_rate = tf.train.exponential_decay(
        initial_learning_rate,
        batch,
        num_decay_steps,
        decay,
        staircase=True
    )
    #采用梯度下降优化损失函数
    optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(
        loss,
        global_step=batch,
        var_list=var_list
    )
    return optimizer
#
#7定义GAN类
class GAN(object):
    def __init__(self, data, gen, num_steps, batch_size, log_every):
        self.data = data#输入数据服从真实分布
        self.gen = gen #数据是生成器
        self.num_steps = num_steps #步长
        self.batch_size = batch_size#12
        self.log_every = log_every #间隔多少输出
        self.mlp_hidden_size = 4 #神经网络隐层神经元的个数
        
        self.learning_rate = 0.03#学习率

        self._create_model()#运行定义的网络模型

    def _create_model(self):
         #8、额外增加了一个网络，为了判别器使用
        with tf.variable_scope('D_pre'):
            self.pre_input = tf.placeholder(tf.float32, shape=(self.batch_size, 1))#真实数据
            self.pre_labels = tf.placeholder(tf.float32, shape=(self.batch_size, 1))#数据标签
            D_pre = discriminator(self.pre_input, self.mlp_hidden_size)#每层有8个神经元，判别器对数据做判别
            self.pre_loss = tf.reduce_mean(tf.square(D_pre - self.pre_labels))#计算损失值
            self.pre_opt = optimizer(self.pre_loss, None, self.learning_rate)#损失值优化

        # This defines the generator network - it takes samples from a noise
        # distribution as input, and passes them through an MLP.
        with tf.variable_scope('Gen'):
            self.z = tf.placeholder(tf.float32, shape=(self.batch_size, 1))#输入噪声数据
            self.G = generator(self.z, self.mlp_hidden_size)#噪音数据在生成器模型生成的假数据

        # The discriminator tries to tell the difference between samples from the
        # true data distribution (self.x) and the generated samples (self.z).
        #
        # Here we create two copies of the discriminator network (that share parameters),
        # as you cannot use the same network with different inputs in TensorFlow.
        with tf.variable_scope('Disc') as scope:
            self.x = tf.placeholder(tf.float32, shape=(self.batch_size, 1))
            self.D1 = discriminator(self.x, self.mlp_hidden_size)#判别器对真实数据做训练
            scope.reuse_variables()#表示这两个网络一样，只是变量重新输入的意思
            self.D2 = discriminator(self.G, self.mlp_hidden_size)#判别去对生成数据做训练

        # Define the loss for discriminator and generator networks (see the original
        # paper for details), and create optimizers for both
        self.loss_d = tf.reduce_mean(-tf.log(self.D1) - tf.log(1 - self.D2))#判别器损失函数
        self.loss_g = tf.reduce_mean(-tf.log(self.D2))#生成器损失函数

        self.d_pre_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='D_pre')#从一个集合中取出权重变量和常数b
        self.d_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Disc')
        self.g_params = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Gen')
        #利用优化器不断地优化self.loss_d，和self.loss_g
        self.opt_d = optimizer(self.loss_d, self.d_params, self.learning_rate)#优化器优化后得损失函数
        self.opt_g = optimizer(self.loss_g, self.g_params, self.learning_rate)
    #模型训练函数
    def train(self):
        with tf.Session() as session:
            tf.global_variables_initializer().run()#初始化全局变量

            # pretraining discriminator
            num_pretrain_steps = 1000#预训练网络迭代1000次
            for step in range(num_pretrain_steps):
                #self.pre_input = tf.placeholder(tf.float32, shape=(self.batch_size, 1)) self.pre_labels
                d = (np.random.random(self.batch_size) - 0.5) * 10.0 #self.pre_input
                labels = norm.pdf(d, loc=self.data.mu, scale=self.data.sigma)#norm.pdf正太概率密度函数
                pretrain_loss, _ = session.run([self.pre_loss, self.pre_opt], {
                    self.pre_input: np.reshape(d, (self.batch_size, 1)),
                    self.pre_labels: np.reshape(labels, (self.batch_size, 1))
                })
            #将pre-training的权重拷贝
            self.weightsD = session.run(self.d_pre_params)
            # copy weights from pre-training over to new D network
            for i, v in enumerate(self.d_params):
                session.run(v.assign(self.weightsD[i]))

            for step in range(self.num_steps):
                # update discriminator先优化判别网络,真实数据x和虚假数据一起输入判别网络
                x = self.data.sample(self.batch_size)#self.batch_size作为N
                z = self.gen.sample(self.batch_size)
                loss_d, _ = session.run([self.loss_d, self.opt_d], {
                    self.x: np.reshape(x, (self.batch_size, 1)),
                    self.z: np.reshape(z, (self.batch_size, 1))
                })

                # update generator，优化生成器网络
                z = self.gen.sample(self.batch_size)
                loss_g, _ = session.run([self.loss_g, self.opt_g], {
                    self.z: np.reshape(z, (self.batch_size, 1))
                })

                if step % self.log_every == 0:
                    print('{}: {}\t{}'.format(step, loss_d, loss_g))                
                if step % 100 == 0 or step==0 or step == self.num_steps -1 :
                    self._plot_distributions(session)#每个100次输出图像

    def _samples(self, session, num_points=10000, num_bins=100):
        xs = np.linspace(-self.gen.range, self.gen.range, num_points)#XS（-8，8）
        bins = np.linspace(-self.gen.range, self.gen.range, num_bins)

        # data distribution
        d = self.data.sample(num_points)#随机生成10000个高斯点真实数据
        #真实的数据分布
        pd, _ = np.histogram(d, bins=bins, density=True)#bins指定统计的区间个数，也就是每间隔100累计输出d的和

        # generated samples
        zs = np.linspace(-self.gen.range, self.gen.range, num_points)
        g = np.zeros((num_points, 1))#初始化为0
        #//当它是除法，取整（不四舍五入）就好,self.G去拟合正真的数据
        for i in range(num_points // self.batch_size):
            g[self.batch_size * i:self.batch_size * (i + 1)] = session.run(self.G, {
                self.z: np.reshape(
                    zs[self.batch_size * i:self.batch_size * (i + 1)],
                    (self.batch_size, 1)
                )#训练好的self.G生成器去拟合数据d
            })
        pg, _ = np.histogram(g, bins=bins, density=True)

        return pd, pg

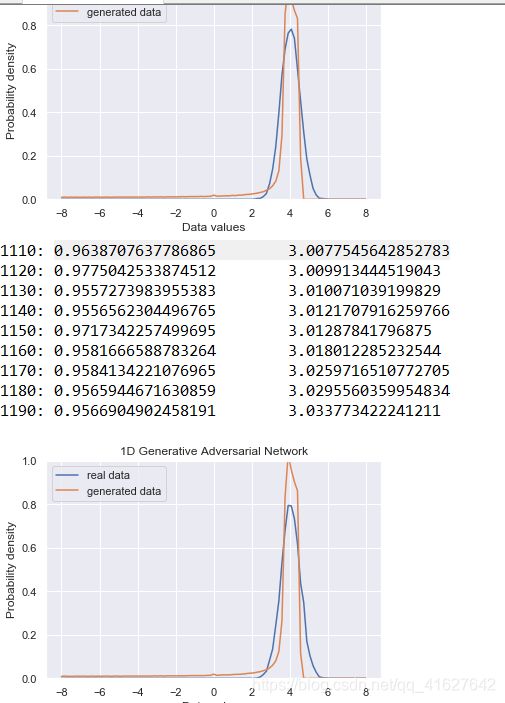
    def _plot_distributions(self, session):
        pd, pg = self._samples(session)
        p_x = np.linspace(-self.gen.range, self.gen.range, len(pd))
        f, ax = plt.subplots(1)
        ax.set_ylim(0, 1)
        plt.plot(p_x, pd, label='real data')
        plt.plot(p_x, pg, label='generated data')
        plt.title('1D Generative Adversarial Network')
        plt.xlabel('Data values')
        plt.ylabel('Probability density')
        plt.legend()
        plt.show()
        
def main(args):
    model = GAN(
        DataDistribution(),
        GeneratorDistribution(range=8),
        args.num_steps,#迭代1200次
        args.batch_size,#迭代12
        args.log_every,#格10次打印一下LOSS
    )
    model.train()#模型训练


def parse_args():
    parser = argparse.ArgumentParser()
    parser.add_argument('--num-steps', type=int, default=1200,
                        help='the number of training steps to take')
    parser.add_argument('--batch-size', type=int, default=12,
                        help='the batch size')
    parser.add_argument('--log-every', type=int, default=10,
                        help='print loss after this many steps')
    return parser.parse_args()


if __name__ == '__main__':
    main(parse_args())