线性代数(六)——二次型
文章目录
- 前言
- 二次型是什么?
- 二次型的表示
- 合同矩阵与合同二次型
- 正定二次型、正定矩阵
- 二次型的题型
前言
一直对二次型和线性代数的关系不解,导致一系列的知识点因为没有理解而常常忘记。 在这里对二次型进行梳理,希望可以加深对二次型的印象。二次型是什么?
二次型的目的,是利用矩阵来研究二次方程。
所以它和线性代数本质的关系不大,可以看作是线性代数的一种应用。
二次型:n个变量的一个二次齐次多项式称为n个变量的二次型。
所以我们很自然的想到既然利用矩阵来研究二次方程,那么二次型肯定要用矩阵表示吧。
矩阵表示:
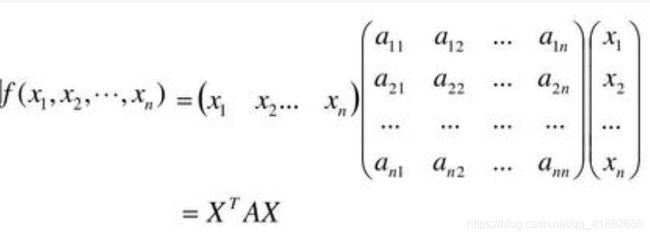
注意:因为 x 1 x 2 = x 2 x 1 x_1x_2 = x_2x_1 x1x2=x2x1,所以二次型的对应矩阵必须是对称阵,只有对应矩阵为对称阵时,二次型的对应矩阵才是唯一确定的。并且我们这一章主要研究实矩阵,所以二次型在这个阶段都是实对称矩阵。
这样就和上一节接上了,实对称矩阵必定可相似对角化,且有 Q − 1 A Q = Q T A Q = Λ Q^{-1}AQ = Q^TAQ = Λ Q−1AQ=QTAQ=Λ。这又和我们马上要讲的合同矩阵相关(实对称矩阵A必定既相似又合同于对角阵)。
二次型的表示
就是把齐次二次多项式进行分类。二次型 f ( x 1 , x 2 , x 3 , x 4 , . . . , x n ) f(x_1,x_2,x_3,x_4,...,x_n) f(x1,x2,x3,x4,...,xn)里面可以分为平方项( x i 2 x_i^{2} xi2)和混合项( x i x j x_ix_j xixj)。
- 只有平方项没有混合项的二次型叫做标准形。
- 只有平方项没有混合项,且平方项的系数只有 1 , 0 , − 1 1,0,-1 1,0,−1时,称作规范形。
定理1:任何一个二次型 f f f,必存在一个正交变换 x = Q y x = Qy x=Qy,其中Q为正交阵,使得二次型化为标准型。
因为二次型是实对称矩阵嘛,且有 Q − 1 A Q = Q T A Q = Λ Q^{-1}AQ = Q^TAQ = Λ Q−1AQ=QTAQ=Λ。中间只剩一个 Λ Λ Λ,便是标准型,标准型的系数为矩阵的特征值。
因为二次型是实对称矩阵嘛,且有 Q − 1 A Q = Q T A Q = Λ Q^{-1}AQ = Q^TAQ = Λ Q−1AQ=QTAQ=Λ。中间只剩一个 Λ Λ Λ,便是标准型,标准型的系数为矩阵的特征值。
定理2:任何一个二次型 f f f,通过配方法必存在一个可逆线性变换 x = C y x = Cy x=Cy,其中Q为可逆矩阵,使得二次型化为标准型。
将二次型变为标准形有两种方法,正交变换和配方法。其中通过正交变换,标准型的系数正好是矩阵的特征值,通过配方法,矩阵的系数不一定是特征值。即二次型的标准形是不唯一的,二次型的规范形是唯一的。
要熟练掌握这两种转化的方法,这是二次型中经典的计算题目。
合同矩阵与合同二次型
定义: 设A、B是两个n阶矩阵,若存在可逆阵C,使得 C T A C = B C^TAC=B CTAC=B,则称A合同于B。
充要条件: 矩阵A、B合同当且仅当对应的二次型有相同的正负惯性指数(惯性定理)且 r ( A ) = r ( B ) r(A) =r(B) r(A)=r(B)。
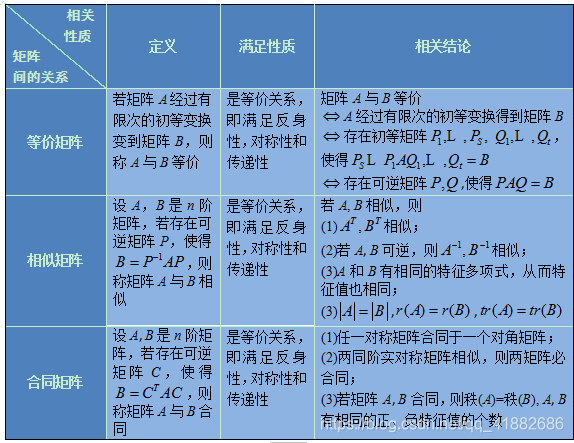
下面摘抄一段来自这里的对矩阵等秩、等价、相似、合同的辨析。
一、矩阵等价、相似和合同之间的du区别:
-
等价,相似和合同三者都是等价关系。
-
矩阵相似或合同必等价,反之不一定成立。
-
矩阵等价,只需满足两矩阵之间可以通过一系列可逆变换,也即若干可逆矩阵相乘得到。
-
矩阵相似,则存在可逆矩阵P使得, A P = P B AP=PB AP=PB。
-
矩阵合同,则存在可逆矩阵P使得, P T A P = B P^TAP=B PTAP=B。
-
当上述矩阵P是正交矩阵时,即 P T = P − 1 P^T = P^{-1} PT=P−1,则有A,B之间既满足相似,又满足合同关系。
二、矩阵等价、相似、合同之间联系:
-
矩阵等秩是相似、合同、等价的必要条件,相似、合同、等价是等秩的充分条件。
-
矩阵等价是相似、合同的必要条件,相似、合同是等价的充分条件。
-
矩阵相似、合同之间没有充要关系,存在相似但不合同的矩阵,也存在合同但不相似的矩阵。
-
总结起来就是:相似=>等价,合同=>等价,等价=>等秩。
三、多说一句:
矩阵等价:
-
同型矩阵而言。
-
一般与初等变换有关。
-
秩是矩阵等价的不变量,其次两同型矩阵等价的本质是秩相等。
矩阵相似:
-
针对方阵而言。
-
秩相等是必要条件。
-
本质是二者有相等的不变因子(超纲)。
矩阵合同:
-
针对方阵而言,一般是对称矩阵。
-
秩相等是必需条件。
-
本质是秩相等且正惯性指数相等,即标准型相同。
通过上述的对比可知,等价关系是三种关系中条件最弱的,合同与相似是特堵的等价关系,若两个矩阵相似或合同,则这两个矩阵一定等价,反之不成立,相似与合同不能互相推导,但是如果两个实对称矩阵式相似的,那一定是合同的。
正定二次型、正定矩阵
判断矩阵A正定的充要条件:
- A的正惯性指数 p = r = n p=r=n p=r=n。
- 矩阵A合同与矩阵E,即 A = D T E D = D T D A=D^{T}ED = D^{T}D A=DTED=DTD。
- A的全部特征值大于0.
- A的全部顺序主子式大于零。
判断矩阵A正定的必要条件:
- A的主对角线元素>0
- ∣ A ∣ > 0 |A|>0 ∣A∣>0
二次型的题型
- 判断两矩阵是否是合同矩阵,矩阵看正负惯性指数,二次型看标准型的正负惯性指数。
- 判断平方和二次型是否是正定矩阵,即判断各子式不能同时为零,即构成的矩阵只有零解。
- 判断抽象矩阵是否为正定矩阵,需要满足可逆、对称和全部特征值大于0的条件,或者利用定义。