最近在看遗传算法,查了很多资料,所以做了如下一些总结,也希望对后面研究的人有些帮助.因为初学GA,文中自己的见解,不一定全对,感兴趣的可以一起探讨.
I 简介
基本概念
遗传算法(Genetic Algorithms, GA)是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
它模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象,在每次迭代中都保留一组候选解,并按某种指标从解群中选取较优的个体,利用遗传算子(选择、交叉和变异)对这些个体进行组合,产生新一代的候选解群,重复此过程,直到满足某种收敛指标为止。
GA的组成:
(1)编码(产生初始种群)
(2)适应度函数
(3)遗传算子(选择、交叉、变异)
(4)运行参数
编码
基因在一定能够意义上包含了它所代表的问题的解。基因的编码方式有很多,这也取决于要解决的问题本身。常见的编码方式有:
(1) 二进制编码,基因用0或1表示(常用于解决01背包问题)
如:基因A:00100011010 (代表一个个体的染色体)
(2) 互换编码(用于解决排序问题,如旅行商问题和调度问题)
如旅行商问题中,一串基因编码用来表示遍历的城市顺序,如:234517986,表示九个城市中,先经过城市2,再经过城市3,依此类推。
(3) 树形编码(用于遗传规划中的演化编程或者表示)
如,问题:给定了很多组输入和输出。请你为这些输入输出选择一个函数,使得这个函数把每个输入尽可能近地映射为输出。
编码方法:基因就是树形结构中的一些函数。
(4) 值编码 (二进制编码不好用时,解决复杂的数值问题)
在值编码中,每个基因就是一串取值。这些取值可以是与问题有关任何值:整数,实数,字符或者其他一些更复杂的东西。
适应度函数
遗传算法对一个个体(解)的好坏用适应度函数值来评价,适应度函数值越大,解的质量越好。适应度函数是遗传算法进化过程的驱动力,也是进行自然选择的唯一标准,它的设计应结合求解问题本身的要求而定。
如TSP问题,遍历各城市路径之和越小越好,这样可以用可能的最大路径长度减去实际经过的路径长度,作为该问题的适应度函数。
遗传算子——选择
遗传算法使用选择运算来实现对群体中的个体进行优胜劣汰操作:适应度高的个体被遗传到下一代群体中的概率大;适应度低的个体,被遗传到下一代群体中的概率小。选择操作的任务就是按某种方法从父代群体中选取一些个体,遗传到下一代群体。
SGA(基本遗传算法)中采用轮盘赌选择方法。
轮盘赌选择又称比例选择算子,基本思想:各个个体被选中的概率与其适应度函数值大小成正比。设群体大小为n ,个体i 的适应度为 Fi,则个体i 被选中遗传到下一代群体的概率为:
遗传算子——交叉
所谓交叉运算,是指对两个相互配对的染色体依据交叉概率按某种方式相互交换其部分基因,从而形成两个新的个体。交叉运算在GA中起关键作用,是产生新个体的主要方法。
1. 单交叉点法 (用于二进制编码)
选择一个交叉点,子代在交叉点前面的基因从一个父代基因那里得到,后面的部分从另外一个父代基因那里得到。
如:交叉前:
00000|01110000000010000
11100|00000111111000101
交叉后:
00000|00000111111000101
11100|01110000000010000
2. 双交叉点法 (用于二进制编码)
选择两个交叉点,子代基因在两个交叉点间部分来自一个父代基因,其余部分来自于另外一个父代基因.
如:交叉前:
01 |0010| 11
11 |0111| 01
交叉后:
11 |0010| 01
01 |0111| 11
3. 基于“ 与/或 ”交叉法 (用于二进制编码)
对父代按位"与”逻辑运算产生一子代A;按位”或”逻辑运算产生另一子代B。该交叉策略在解背包问题中效果较好 .
如:交叉前:
01001011
11011101
交叉后:
01001001
11011111
4. 单交叉点法 (用于互换编码)
选择一个交叉点,子代的从初始位置出发的部分从一个基因复制,然后在另一个基因中扫描,如果某个位点在子代中没有,就把它添加进去。
如:交叉前:
87213 | 09546
98356 | 71420
交叉后:
87213 | 95640
98356 | 72104
5. 部分匹配交叉(PMX)法(用于互换编码)
先随机产生两个交叉点,定义这两点间的区域为匹配区域,并用交换两个父代的匹配区域。
父代A:872 | 130 | 9546
父代B:983 | 567 | 1420 变为:
TEMP A: 872 | 567 | 9546
TEMP B: 983 | 130 | 1420
对于 TEMP A、TEMP B中匹配区域以外出现的数码重复,要依据匹配区域内的位置逐一进行替换。匹配关系:1<——>5 3<——>6 7<——>0
子代A:802 | 567 | 9143
子代B:986 | 130 | 5427
6. 顺序交叉法(OX) (用于互换编码)
从父代A随机选一个编码子串,放到子代A的对应位置;子代A空余的位置从父代B中按B的顺序选取(与己有编码不重复)。同理可得子代B。
父代A: 872 | 139 | 0546
父代B: 983 | 567 | 1420
交叉后:
子代A: 856 | 139 | 7420
子代B: 821 | 567 | 3904
7. 循环交叉(CX)法(用于互换编码)
CX同OX交叉都是从一个亲代中取一些城市,而其它城市来自另外一个亲代,但是二者不同之处在于:OX中来自第一个亲代的编码子串是随机产生的,而CX却不是,它是根据两个双亲相应位置的编码而确定的。
父代A:1 2 3 4 5 6 7 8 9
| | | | |
父代A:5 4 6 9 2 3 7 8 1
可得循环基因:1->5->2->4->9->1
用循环的基因构成子代A,顺序与父代A一样
1 2 4 5 9
用父代B剩余的基因填满子代A:
1 2 6 4 5 3 7 8 9
子代B的编码同理。(循环基因 5->1->9->4->2->5)
遗传算子——变异
变异是指依据变异概率将个体编码串中的某些基因值用其它基因值来替换,从而形成一个新的个体。GA中的变异运算是产生新个体的辅助方法,它决定了GA的局部搜索能力,同时保持种群的多样性。交叉运算和变异运算的相互配合,共同完成对搜索空间的全局搜索和局部搜索。
注:变异概率Pm不能太小,这样降低全局搜索能力;也不能太大,Pm > 0.5,这时GA退化为随机搜索。
1. 基本位变异算子 (用于二进制编码)
基本位变异算子是指对个体编码串随机指定的某一位或某几位基因作变异运算。对于基本遗传算法中用二进制编码符号串所表示的个体,若需要进行变异操作的某一基因座上的原有基因值为0,则变异操作将其变为1;反之,若原有基因值为1,则变异操作将其变为0。
如:变异前:
000001110000000010000
变异后:
000001110001000010000
2. 逆转变异算子(用于互换编码)
在个体中随机挑选两个逆转点,再将两个逆转点间的基因交换。
如:变异前:
1346798205
变异后:
1246798305
运行参数
GA运行时选择的参数应该视解决的具体问题而定,到目前为止,还没有一个适用于GA所有应用领域的关于算法参数的理论。下面是一般情况下使用GA时推荐的参数:
1) 交叉率
交叉率一般来说应该比较大,推荐使用80%-95%。
2) 变异率
变异率一般来说应该比较小,一般使用0.5%-1%最好。
3) 种群的规模
种群规模指的是群体中个体的个数。实验发现,比较大的种群的规模并不能优化遗传算法的结果。种群的大小推荐使用20-30,一些研究表明,种群规模的大小取决于编码的方法,具体的说就是编码串(Encoded String)的大小。也就是说,如果说采用32位为基因编码的时候种群的规模大小最好为32的话,那么当采用16位为基因编码时种群的规模相应应变为原来的两倍。
4) 遗传运算的终止进化代数
个人的想法是,设定一个计数器,如果连续N代出现的最优个体的适应度都一样时,(严格的说应该是,连续N代子代种群的最优个体适应度都<=父代最优个性的适应度)可以终止运算。
也可以简单的根据经验固定进化的代数。
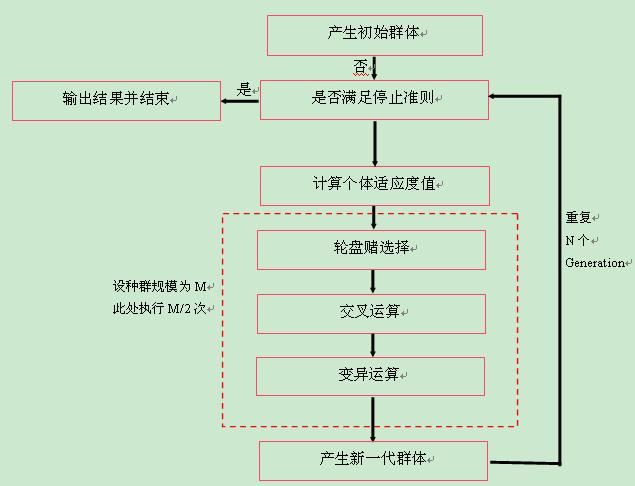
II 运算流程
图中的“是否满足停止准则”便可参照上节中“遗传运算的终止进化代数”
III 灾变与精英主义
灾变
遗传算法的局部搜索能力较强,但是很容易陷入局部极值。引用网上的一段原话:
“那么如何解决遗传算法容易陷入局部极值的问题呢?让我们来看看大自然提供的方案。六千五百万年以前,恐龙和灵长类动物并存,恐龙在地球上占绝对统治地位,如果恐龙没有灭绝灵长类动物是绝没有可能统治地球的。正是恐龙的灭绝才使灵长类动物有了充分进化的余地,事实上地球至少经历了5次物种大灭绝,每次物种灭绝都给更加高级的生物提供了充分进化的余地。所以要跳出局部极值就必须杀死当前所有的优秀个体,从而让远离当前极值的点有充分的进化余地。这就是灾变的思想。”
灾变就是杀掉最优秀的个体,这样才可能产生更优秀的物种。那何时进行灾变,灾变次数又如何设定?
何时进行灾变,可以采用灾变倒计数的方式。如果n代还没有出现比之前更优秀的个体时,可以发生灾变。灾变次数可以这样来确定,如果若干次灾变后产生的个体的适应度与没灾变前的一样,可停止灾变。
精英主义
当利用交叉和变异产生新的一代时,我们有很大的可能把在某个中间步骤中得到的最优解丢失。
精英主义的思想是,在每一次产生新的一代时,首先把当前最优解原封不动的复制到新的一代中。然后按照前面所说的那样做就行。精英主义方法可以大幅提高运算速度,因为它可以防止丢失掉找到的最好的解。
矛盾
由上面看来,灾变与精英主义之间似乎存在着矛盾.前者是将产生的最优个体杀掉,而后者是将最优秀个体基因直接保存到下一代.
应该辩证地看待它们之间的矛盾,两者其实是可以共存的.我们在每一代进行交叉运算时,均直接把最优秀的个体复制到下一代;但当连续N代,都没有更优秀的个体出现时,便可以猜想可能陷入局部最优解了,这样可以采用灾变的手段.可以说,精英主义是伴随的每一代的,但灾变却不需要经常发生,否则算法可能下降为随机搜索了.
当然,每个算法中不一定要用精英主义和灾变的手段,应该根据具体的问题而定.
IV GA的特点
遗传算法的优点:
(1)群体搜索,易于并行化处理;
(2)不是盲目穷举,而是启发式搜索;
(3)适应度函数不受连续、可微等条件的约束,适用范围很广。
(4)容易实现。一旦有了一个遗传算法的程序,如果想解决一个新的问题,只需针对新的问题重新进行基因编码就行;如果编码方法也相同,那只需要改变一下适应度函数就可以了。
遗传算法的缺点:
(1)全局搜索能力不强,很容易陷入局部最优解跳不出来;(可结合SA进行改进,因为SA在理率上是100%得到全局最优的,但搜索代价高)
(2)计算时间长。