叶杰平,美国密歇根大学终身教授,密歇根大学数据研究中心管理委员会成员,美国明尼苏达大学博士毕业,现任滴滴研究院副院长。在NIPS, KDD, IJCAI, ICDM, SDM, ACML, and PAKDD发表多篇论文. 他担任Data Mining and Knowledge Discovery, IEEE Transactions on Knowledge and Data Engineering, IEEE Transactions on Pattern Analysis and Machine Intelligence的编委. 2010年获得NSF CAREER Award。2010,2011,2012年分别获得KDD最佳论文提名,2013年获得KDD最佳论文奖。2014年获得ICML最佳学生论文奖。以下为叶杰平教授所做现场演讲的一部分,主要对稀疏和低秩约束在机器学习上的应用进行了介绍。
大家下午好,非常高兴,能够和大家一起,分享低秩和稀疏两种方法,主要会讲解一些在large-scale方面的应用,也会稍微提一下滴滴的一些应用,大部分我讲的很多应用,都会用用在特征约减,与很多问题如滴滴,都会有很多样本,每天都有上千万的大规模数据量不同,很多问题有成千上百万维度的特征,如何对特征进行稀疏和低秩约束,是我们今天要讲的主要内容,今天的报告主要针对模型介绍,具体应用可以下面查阅文献,不会具体讲解。
本次报告主要对一些基础的稀疏模型,以及结构的稀疏模型进行讲解,并会简单介绍低秩的模型,以及一些优化加速算法,最后会给大家讲一下large-scale,以及如何将这些算法用在大规模的数据上。
大家可能都对稀疏的含义比较了解,这里的稀疏,可能表示模型特征的稀疏,也可能表示数据的稀疏,数据稀疏主要是指文件的keyword比较稀疏,这里我们主要是指模型特征的稀疏,比如说一维的线性回归或者矩阵,这里的稀疏就是指模型的特征会比较少。
我们引入一个正则的概念,通过一个简单的线性拟合,建立一条线来拟合样本点,假设有一个M阶的多项式来进行拟合,那么有M+1个参数需要估计,我们希望利用这个方式来进行预测优化,找到一个系数使得误差最小。对于每一点我们有一个预测值y,一个ground truth,通过优化M+1个变量,使得y与ground truth之间差异最小。当M为0的时候我们可以知道这是一条直线,当M等于3的时候就变成了一条曲线,等等。
通过实验结果。我们可以看到训练误差在M很大的时候很小,而测试误差很大,这也就是非常常见的过拟合的问题,M太小的时候,模型太简单,训练误差和测试误差都很大,这也就是欠拟合的问题,M取中间值时才会非常合适,这过拟合和欠拟合也是两个非常常见的机器学习问题。我们对这些系数进行分析,可以看到在,当M等于9的时候,系数非常大,也可以发现,如果overfit的情况,如果稍微抖动的话,会对系数有非常大的影响,自然而然的,我们需要对我们的模型加一个正则项,从而通过控制系数的大小,向可以接受的误差逼近,通过数据拟合项的范式约束,使得模型的误差变小,模型能够更加的拟合数据,再加上一个控制系数的正则项,使得模型的参数更加稳定。超参数λ用来控制稀疏的程度,当超参数λ等于0时,模型也就退化成了一般的线性回归,λ一般需要通过调节参数学习出来,通过实验可以发现,λ比较小的话模型就会容易过拟合,λ比较合适的话模型就会比较稳定。
通常,我们利用正则项来控制参数W的大小,这里可以用q norm作为正则项,来保证W比较小,当q=2的时候能够保证W有一个光滑的解析解,q=1时,正则项是一个凸函数,且能够使得W稀疏;q在大于等于1 的时候,该模型仍然是一个凸函数,好处就是能够保证找到最优解,q小于1时,模型就变得非凸了,但是能够找到一个稀疏解。
自然地,我们就要思考为什么L1范式能够得到一个稀疏解,这里我们给出一个简单的例子,前面时loss函数,后面是正则项,可以看到一范式为凸但不可微,会在x=0时取到极值点,二范数在零点可微,但是不一定在零点取得极值点,另外一种对于一范数稀疏的解释是通过等高线的方式,可以发现一范数的约束能够使得loss函数在零点相交,而二范数是一个球,不一定与loss函数在零点相交,从而一范数能够使得解稀疏。
一范数最经典的就是96年的LASSO问题,我们有数据矩阵A,每一行代表样本,列代表特征,有标签y,可以代表分类和回归问题,我们这里用一个简单的线性模型取取预测y,呢么Ax-y就是一个拟合项,一范数就是正则项,使得x的系数稀疏,从而去掉一些无关项,如对疾病不相关的基因,从而增强了模型的可解释性,自动做了特征选择,有效的避免过拟合,这样子,稀疏可以同时选择特征,并且建立了模型。下面我们会讲一些结构性的计算,这个模型能够同时作特征选择和进行回归或分类。这里我们举一个在MRI上面的应用。利用简单的logit回归,加上一个稀疏先验,利用MRI图像进行病人和正常人的分类,并且同时实现了探寻哪一些脑区信号与疾病的相关与否,找到了与疾病相关的一些特征,之前提到的y都是比较简单的,只有一列,但是很多场景下,y可能有很多值,我们特征可能时很多的特征,y可能是1维的比如说有病无病,也可能多维的比如说每个脑区的一些判别,这样不仅每个点都是多维的,label也可能是有很多维,这样就是一个两边都是多维的big data问题,模型也从从一个一列,变成了一个矩阵,扩展了一个平方的关系。如果不增加正则项,这种问题将会非常难以解决。假设有一千个数据,x和y都是一百万维,这个模型就会是一个非常大的矩阵,如果没有正则项,这个模型将几乎无法求解。需要加入很多的假设,如低秩假设,这个模型也就可以对数据矩阵进行分解,也就使得我们的维度降低,最后在假设稀疏,进一步降低了系数的维度,现在的数据量都比较低,特征特别大,我的一个合作者进行了一个比较大的项目,把所有的数据整合在一起,有两三万个数据,但仍然不算很多,未来的数据如果越来越大的话,模型会越来约精确,现有数据不足,所以只能对模型加入很多假设,从而保证模型的有效性,当然,数据还是第一重要的。
系数学习在很多领域中都有很广泛的应用,如生物医学,图像处理,neuroscience,机器学习等等,我们最终的目的是找到一个超参数,一个常用的方法是使用交叉检验,在一个广泛的超参数空间中,选择一个最优的超参数,这种方法可能会存在一种缺陷,一个更好的方法是使用stability selection. 相当于对每个数据进行子采样,然后进行多次筛选,选择最好的参数,具体的可以在文章中查阅,里面有很强的理论证明。它会对问题进行很多子采样,所以会进行很多次的lasso求解,因此需要一个特别快的算法,这也是我们今天主要要讲得,如何在大规模的数据上进行计算。
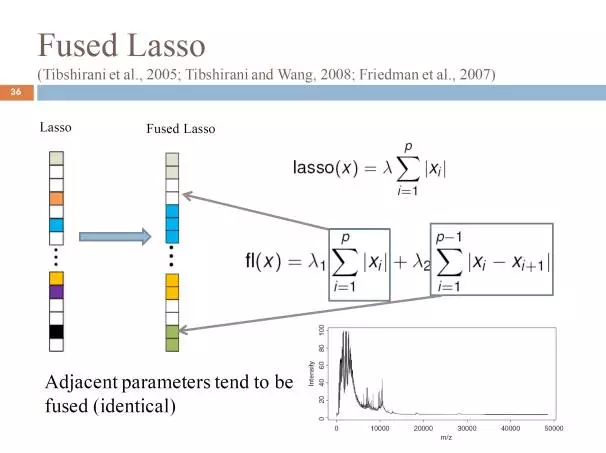
刚刚对基础进行了讲解,下面我们对几个模型进行讲解,刚刚提到过LASSO可以同时解决提取参数和预测两个任务,并且具有是的提取的特征具有理论可解释性,同时非常容易推广。我们知道,很多特征是有结构的,特征与特征之间并不是独立的,特征之间是可以分组,我们首先介绍一些结构LASSO,这里给出一个例子,特征之间会有光滑性,我们给出了一个所有脑区的特征,我们可以发现向邻近的点会比较类似,特征的光滑性有时间和空间上的光滑性,比如说,相邻时刻之间的数据以及相邻空间的数据是具有相似性的,所以很多问题都是有光滑性的,也会有一些问题具有一些树的结构,以及一些问题可能具有一些网的结构,得到特征值之间的相似性。当我们获得我们的这些特征之间的先验知识之后,如果对lasso进行推广,利用我们的特征之间的信息,结构的lasso也就应运而生。和lasso类似,损失函数可以根据问题相关设计,如logit回归或者最小二乘回归等等,来表示对数据的拟合程度,重点是如何设计我们的penalty,lasso是L1-norm,仅仅是稀疏,特征之间没有任何假设,但是如果我们有特征直接结构的先验知识,那么我们可以在正则项这里进行推广,一般是利用一个凸的方法,来得到我们需要的结构,这里我们根据结构的先验信息,有Fused LASSO(光滑性),Graph LASSO(图结构), Group LASSO(组结构)以及树结构LASSO(树结构)。
考虑到光滑性,可以通过增加一项差分项的方式,有效的保证相邻的两项是相近的,参数是类似的,最终的结果我们会发现最后的结果相邻的系数都是相同的。每一段都是一个常数,而且很多都是稀疏的,这样子就能够简化模型,降低模型的复杂性,同时实验发现,这种方式能够有效的提升符合这种特点的数据的效果。
第二个推广是考虑到很多数据的特征是相关的,比如说是蛋白质的特征之间是相关的,类似fused LASSO,我们增加一个penalty,使得相关的特征具有相同的结构,考虑到相关性可能是反向,可以增加一个绝对值解决这个问题,解决相关但是符号不一致的问题,这个问题会稍微复杂一点,是一个非凸问题,同样在试验中,我们发现,加了graph结构之后,模型效果会好很多。
第三个推广是很多特征会有一种组的结构,最典型的应用就是在脑影像的分析中,很多脑区或者体素之间有一定的组约束的,同时滴滴也有很多场景,如司机,终点,天气等等,还有基因的categorical variable。我们可以很多特征必须放在一组里才有一定的意义。因此group LASSO也就应运而生来解决这种存在组结构的问题, 解决思路是,通过L1-norm来筛选特征,如果有这种组的先验信息,可以先提供对这些组先计算Lp-norm,在计算这几个group的L1-norm,在通过加入这种形式的penalty,会使得相同组的要么全为零,妖媚全部被调出来。具体的应用就是multi-task,假设我们有k个task,每一行做一个group,然后用L1Lp做penalty,这样会使得该特征对于所有的task要么都被提取,或者同时不被提取。比如说手写字符识别,有两种极端是,一种是把所有的字母放在一起,进行训练,另外一种是每个人建立一个不同的模型,第一个模型不能有很好的泛化性能,第二个模型会导致模型很复杂,而且每个人的数据可能不足,而multi-task是介于两者之间的一种方式,希望建立每个人的模型是相关的,每个模型提取的特征是一样的,可以看到,字符识别的结果相较之前的两种方法都要好。
很多时候,简单把各个特征简单的分成各个组可能是不够的,特征之间可能会有一些更加精细的结构,比如说分层的结构,这样子特征之间会有更多的信息,如果特征的相似性具有一种树结构,那么简单的使用group LASSO 效果就不好,因此我们就需要引入树的特征,这样会使得模型有更好的效果,这里简单举一个例子,假设每个样本是一个图,最上层就是整个脑区,在树的最顶端,如果我们对脑区进行划分,类似的可以继续的继续划分,一直到体素,这样子就会组成一个树的结构,如果两个体素在同一个树下,它们的特征就会很类似,如果它们不类似,那么就说明它们距离很远,这样子就是一个树的特征。我们也就可以基于此,建立一个树的lasso,每一层做一个group 的LASSO,这样会使得如果上层为零,那么,该结点的所有连接都会为零,在脑影像上面的实验也表明,树约束能够使得我们挑出的特征聚集在某一些脑区,使得模型结果更加具有可解释性。
下面讲一下低秩模型,这里会将的快一些,我最后会讲一些screening,有很多问题都可以用矩阵来表示,很多时候,矩阵中的一些值是未知的,因此需要用观测值去预测丢失值,比如说图像,可能会有一些图像被树覆盖,需要用观测值去预测被遮挡的部分。或者说collaborative filter,行代表用户,列代表等级,每个用户被要求给电影打分,但不是所有的用户都对所有的电影打分,所以我们需要去预测这些缺失的数据。再考虑netflix问题,很多打分都是丢失的,我们如何用有限的数据来预测大量的缺失的数据。如果不做任何假设,这个问题是很难解决的,因此,我们引入低秩假设。对于每个问题,首要核心的问题是少量的低秩的。Rank可以通过SVD分解,通过非零的奇异特征数就是矩阵的rank。我们希望的模型就是希望矩阵的秩比较小。
低秩模型与稀疏模型比较类似,这里我们假设红色的是观测点,白色为缺失点,X是我们需要预测的,该问题第一项为数据拟合项,我们需要M与X类似,同时希望我们填补之后的X能够保持低秩特性,是的主要因素数量比较少,并用λ控制这个数量。由于rank是非奇异的,因此问题的求解会存在问题,是一个NP-难问题,常用的方法使用rank的上确界trace-norm来逼近它,同时trace-norm是一个连续的凸问题,使得问题更加容易求解,且能够使得奇异值变为零,最终低秩。
最近也有很多方法将其转变成为非凸的问题,将X转换成U和V相乘的形式,从而使得X的秩降低,通过求解U和V对X进行预测,,通过不断的固定U求解V在固定V求解U,最终收敛,这样求解更加快速。
还有一种方法是将X转换成类似SVD的形式,把矩阵转换为向量的问题,将矩阵X转化成r个秩等于1的矩阵相乘再相加,对X进行预测,使得矩阵X的秩小于r,从而保证低秩。
下面我们主要会讲一些优化的算法,比如lasso,结构的稀疏等等,模型大概会有怎么样的优化结果,我们处理的很多问题都是连续凸不可导的问题,主要会讲一些流行的解放,并介绍一些加速算法。
我们的问题几乎都可以分解成为loss 和penalty的形式,假设loss是可微的凸问题,penalty是不可到的凸问题,目前主要有以下解决方法:1)将不光滑的问题转化为光滑的问题,2)坐标下降方法,3)ADMM算法,4)次梯度下降,5)梯度下降,6)加速梯度下降等等。下面会主要讲解坐标下降以及ADMM。
坐标下降算法的想法很简单,假设模型有一百万维的数据,需要优化一百万维的数据,那么我们会每次只优化一维的特征,依次优化,不断迭代,一直到收敛。很多大问题的解法可以用这种方法很快速的求解。
当问题是光滑且凸的时候,坐标下降算法一定可以收敛,当问题不光滑的时候,当不光滑的部分是可分的,那么坐标下降算法也可以收敛。坐标下降算法的有点事可以很容易的计算,同时能够非常快的收敛。但是缺点是当loss比较复杂时,会很明显的降低速度,且不一定有解。
快速讲一下ADMM,ADMM算法假设有两个变量fx+gz,然后给定一个约束,将其放入两组变量,我们可以首先是生成增广拉格朗日,再增加penalty,从此就可以通过反复依次对xzy优化对模型求解。
ADMM对于大规模的问题非常有效,能够将复杂问题变成一个较为容易求解的问题,我们以lasso为例,一个传统的LASSO是有一个loss加一个一范数约束,我们将x变成z,所以约束为z=x,就可以生成如下增广拉格朗日模型:
对于xzu的求解都会发现非常容易求解,也就将一个lasso一个复杂的非凸问题,通过几个简单的更新,就可以对齐求解,ADMM的优点是解释非常简单,如果模型非常复杂,能够非常有效的处理,同时可以分布式的进行计算,并对低秩可以很快的学习,缺点就是收敛比较慢。
下面介绍以下大家熟悉的梯度下降法,可以对光滑问题非常有效的求解,同过不断的沿着梯度方向迭代,一定能求出凸光滑问题的解。但是我们需要关注的问题时如何将梯度下降将其推广到非光滑的问题上面,想法非常自然,考虑一个梯度下降算法,我们可以通过另外的方式将其表达,对其进行一个低阶的逼近,用一个低阶的taylor展开做一个一阶的逼近,再利用正则项,使得x再可行域范围内。然后我们对M函数找到最优化的x,然后不断迭代。通过数学验证我们也可以发现最优的x刚好等于梯度下降的值,即这种方式时梯度下降的另外一种表达方式,将梯度下降转化为了一个有优化问题。
通过低阶泰勒展开,加正则,以及不光滑的部分,将梯度下降转变为了一个能求解可微不可导的方法,没有改变速度,并且能够保证收敛到最优解。然后我们可以对其进行加速,之前讲得时再当前点进行梯度下降,我们可以通过引入下一个点,并对其进行线性组合,从而使得其加速,再si上进行梯度下降,可以证明这样的收敛速度是最优的。
加速梯度下降的关键问题是penalty,如果penalty简单,那么模型一定有解细节,如果penalty复杂,那么模型会很复杂,每一步的cost会很大,当L1norm时,或者trace-norm都可以将其转化为一个proximal操作,存在一个很好的解析解,从而使得模型的解稀疏或者低秩。
最后讲一下screen,刚刚讲了很多优化的解法,比如说CD ADMM GD 等等,这些可以解小到中型的问题,非常有效,但是对于大规模的数据,做交叉检验,训练,就会有很高的代价。那么我们动机就是如何使用稀疏加快我们的算法,加快的原因主要有,模型的特征非常多,模型可能复杂,可能需要很多次交叉严重,并且需要对很多特征进行统计上的验证。都会非常复杂,因此我们需要加快我们的算法。
自然的想法就是对数据进行约减,将该问题压缩,从而有效的加快算法,把大问题变为小问题,最近有很多这方面的研究,比如说随机的选择特征,或者做heuridtic,通过将相关性大的特征选择出来,从而达到数据压缩,但这种方法都不能达到一个精确的结果。所以有一些方向是尽可能的保证与精确解的误差最小,这里我要介绍一种方法,这种方法没有误差,核心思想是将维度约减之后,保证和不screen之前的解一样,我们用lasso做一个例子,data是需要约减,假设系数稀疏,这里我们假设大部分的数据系数是等于零的,那么我们可以直接去掉这些数据,从而有效的实现对数据的约见,screen的核心是在不求解lasso的情况下,尽可能找到系数为零的参数,实现对数据约减。核心方法是是第一步找到对偶解,Lasso的对偶问题有很好的几何解释,也就是对数据做一个投影,有时有些对偶解,可能不好求解,但是可以通过一个近似解,来对数据进行screen,第二补在将系数可能为零特征screen掉,第三步最后在小的数据上进行训练,这样就可以非常快速求解。
大家知道从primal到duel有一个KKT,我们给定一个KTT θ是对偶变量,xi是特征,在不同sample的值,我们需要关心的是那些β等于0,从而能够有效screen数据,我们发现,当θx<1时,βi一定等于0,这也是我们需要利用到的核心,但是这里的θ是不知道的,因此我们需要找到一个近似解。当在一个邻域内,max θx<1,那么最优解一定给在这个邻域内。这个区域需要越简单越小越好。实验发现模型,在不加入新的资源的情况下,运算加速可以有几百倍,而精度几乎不变化。而且该screen方法可以用在别的模型上,对其进行加速。
刚刚我们讲的是特征很大,对其进行压缩,更加流行的问题是样本是无穷大,但是特征并不多,因此需要对样本的数量进行screen,比如说SVM,我们需要进行分类,需要找到一个超平面,吧两类分开,最重要的是如何找到支持向量,问题是如何在没有求解svm的时候找到支持向量,因此我们可以用screen找到支持向量,去掉对问题没有影响的点,从而对数据进行压缩,快速找到超平面。LASSO是在挑样本,SVM是用来挑样本,都是通过一个screen操作,去掉无用样本或者特征,问题减少,从而速度加快。与lasso类似,我们首先对对偶问题进行预估,再接两个优化问题,找到一个邻域,从而找到解得判断,从而加快速度。当然也会遇到一些特征和样本都大的问题,我们可以同时对样本和特征都进行压缩的情况下,同时保证解一样,同时这个方法很容易推广。