工业机械臂直线插补相关记录
本文仅记录一下实验室工业机械臂直线插补的相关情况,若有出错之处,还请见谅。
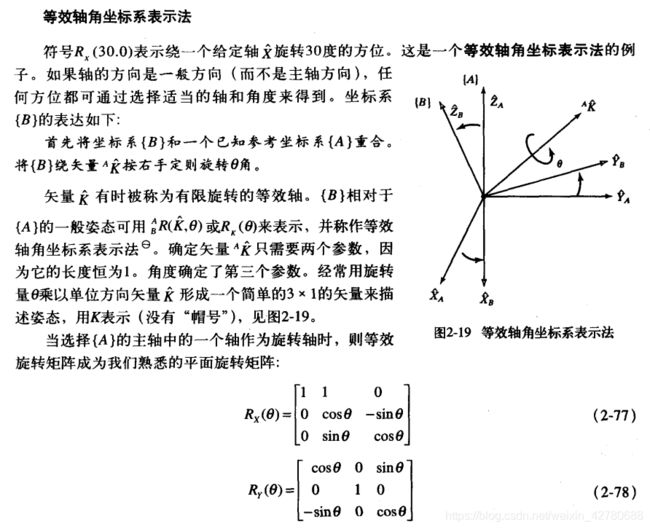
我们知道,刚体的姿态描述有多种方法,像旋转矩阵、欧拉角、四元数、旋转向量表示等。在笛卡尔空间机械臂的末端轨迹规划中,就直线插补来说,我们实验室试过了几种姿态规划方法,最早使用的是等效轴角坐标系表示法,主要原理如下(摘自机器人学导论):
实验室机械臂的直线插补思路大致是这样的:
1、求取两点之间的距离;
2、求取两点姿态之间的变换矩阵,将变换矩阵转化为等效轴角坐标系表示;
3、决定插补次数;
4、线性插值距离和等效角度,将两者结合起来,实现直线插补。
由于用等效轴角坐标系表示会存在奇异点问题,这点需要特别注意。
下面我用matlab仿真查看该直线插补算法在关节空间内位置、速度、加速度的情况,贴上仿真代码:
主文件:
Linear_interpolation.m
clc; %清屏
clear; %清除变量
%robootics_toolbox-9.10版本中连杆长度单位是m,不是mm,需要注意,否则绘图可能会卡死
%%%%%%%%%%%% 工业机械臂DH模型 %%%%%%%%%%%
% theta D A alpha %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
L1=Link([ 0 0 0 0 ],'modified');
L2=Link([ 0 0 0.030 -pi/2 ],'modified');
L3=Link([ 0 0 0.2625 0 ],'modified');
L4=Link([ 0 0.2685 0.052 -pi/2 ],'modified');
L5=Link([ 0 0 0 pi/2 ],'modified');
L6=Link([ 0 0 0 -pi/2],'modified');
R=SerialLink([L1 L2 L3 L4 L5 L6],'name','M');
q1 = [-0.3023, 48.327-90, 46.198-90, -0.001, -7.1993, 0.000]; %起始位置
q2 = [-0.271, 95.150-90, 39.975-90, -0.114, -54.287, 0.000]; %终止位置
deg2rad = pi/180; %角度转弧度系数
q1 = q1*deg2rad; %转化为弧度
q2 = q2*deg2rad;
source_matrix = R.fkine(q1) %正解求出起始位姿
target_matrix = R.fkine(q2) %正解求出终止位姿
k = 4186.811;
b = 1349.923950;
v_length = target_matrix.t-source_matrix.t %位移向量
length = norm(v_length) %向量模长,两点间距离
step_num = round(k * length + b) %用函数根据长度,计算出较为合理的插补点数量,取整数部分
[angle_axis, angle] = Compute_Equivalent_Axis_Angle(source_matrix.R, target_matrix.R); %姿态由旋转矩阵转化为等效轴角表示
% step_num = 10 %test
v_increment = v_length / step_num; %计算两点间XYZ方向的增量向量
angle_increment = angle / step_num;
arry_len = step_num+2; %数组一维大小
q_t = zeros(arry_len, 6); %初始化矩阵容量大小
time = zeros(arry_len, 1);
v = zeros(arry_len, 6);
ts = 0.005 %5ms,插补时间间隔
%初始化
q_t(1,:) = q1;
v(1,:) = 0 ;
time(1) = 0;
%开始直线插补
for i=1:1:step_num
v_step = source_matrix.t + v_increment * i; %计算XYZ方向的插补位置
run_angle = angle_increment * i; %计算姿态等效插补角度
equivalent_matrix = Change_Equivalent_Axis_Angle_to_Matrix(angle_axis, run_angle);
pose_matrix = SE3(source_matrix.R * equivalent_matrix, v_step); %创建SE3对象
q_t(i+1,:) = R.ikine(pose_matrix); %逆解结果
time(i+1) = i*ts;
end
q_t(arry_len,:) = q2; %设置为与q_t(step_num+1,:)相同以求取速度时此时为零
v(2:arry_len,:) = diff(q_t,1,1)/ts; %差分关节位置求取速度
time(arry_len) = (step_num+1)*ts; %此处只是为了下面画图时向量维度一致
a = diff(v,1,1)/ts; %差分速度求取加速度
figure(1)
subplot(3, 2, 1)
plot(time, q_t(:,1), 'r', 'LineWidth', 1.5)
ylabel('position 1 axis')
grid on
subplot(3, 2, 2)
plot(time, q_t(:,2), 'r', 'LineWidth', 1.5)
ylabel('position 2 axis')
grid on
subplot(3, 2, 3)
plot(time, q_t(:,3), 'r', 'LineWidth', 1.5)
ylabel('position 3 axis')
grid on
subplot(3, 2, 4)
plot(time, q_t(:,4), 'r', 'LineWidth', 1.5)
ylabel('position 4 axis')
grid on
subplot(3, 2, 5)
plot(time, q_t(:,5), 'r', 'LineWidth', 1.5)
ylabel('position 5 axis')
grid on
subplot(3, 2, 6)
plot(time, q_t(:,6), 'r', 'LineWidth', 1.5)
ylabel('position 6 axis')
grid on
figure(2)
subplot(3, 2, 1)
plot(time, v(:,1), 'b', 'LineWidth', 1.5)
ylabel('velocity 1 axis')
grid on
subplot(3, 2, 2)
plot(time, v(:,2), 'b', 'LineWidth', 1.5)
ylabel('velocity 2 axis')
grid on
subplot(3, 2, 3)
plot(time, v(:,3), 'b', 'LineWidth', 1.5)
ylabel('velocity 3 axis')
grid on
subplot(3, 2, 4)
plot(time, v(:,4), 'b', 'LineWidth', 1.5)
ylabel('velocity 4 axis')
grid on
subplot(3, 2, 5)
plot(time, v(:,5), 'b', 'LineWidth', 1.5)
ylabel('velocity 5 axis')
grid on
subplot(3, 2, 6)
plot(time, v(:,6), 'b', 'LineWidth', 1.5)
ylabel('velocity 6 axis')
grid on
figure(3)
subplot(3, 2, 1)
plot(time(1:arry_len-1), a(:,1), 'g', 'LineWidth', 1.5)
ylabel('acceleration 1 axis')
grid on
subplot(3, 2, 2)
plot(time(1:arry_len-1), a(:,2), 'g', 'LineWidth', 1.5)
ylabel('acceleration 2 axis')
grid on
subplot(3, 2, 3)
plot(time(1:arry_len-1), a(:,3), 'g', 'LineWidth', 1.5)
ylabel('acceleration 3 axis')
grid on
subplot(3, 2, 4)
plot(time(1:arry_len-1), a(:,4), 'g', 'LineWidth', 1.5)
ylabel('acceleration 4 axis')
grid on
subplot(3, 2, 5)
plot(time(1:arry_len-1), a(:,5), 'g', 'LineWidth', 1.5)
ylabel('acceleration 5 axis')
grid on
subplot(3, 2, 6)
plot(time(1:arry_len-1), a(:,6), 'g', 'LineWidth', 1.5)
ylabel('acceleration 6 axis')
grid on函数文件:
1、Change_Equivalent_Axis_Angle_to_Matrix.m
%将姿态由等效轴角坐标表示转化为旋转矩阵形式表示
function result_matrix = Change_Equivalent_Axis_Angle_to_Matrix(angle_axis, angle)
result_matrix = eye(3);
cos_angle = cos(angle);
sin_angle = sin(angle);
v_angle = 1 - cos_angle;
kx = angle_axis(1);
ky = angle_axis(2);
kz = angle_axis(3);
result_matrix(1,1) = kx * kx * v_angle + cos_angle;
result_matrix(1,2) = kx * ky * v_angle - kz * sin_angle;
result_matrix(1,3) = kx * kz * v_angle + ky * sin_angle;
result_matrix(2,1) = kx * ky * v_angle + kz * sin_angle;
result_matrix(2,2) = ky * ky * v_angle + cos_angle;
result_matrix(2,3) = ky * kz * v_angle - kx * sin_angle;
result_matrix(3,1) = kx * kz * v_angle - ky * sin_angle;
result_matrix(3,2) = ky * kz * v_angle + kx * sin_angle;
result_matrix(3,3) = kz * kz * v_angle + cos_angle;
end
2、Compute_Equivalent_Axis_Angle.m
%将姿态由旋转矩阵形式表示转化为等效轴角表示
function [axis_angle, angle] = Compute_Equivalent_Axis_Angle(source_matrix,target_matrix)
matrix_multi = source_matrix' * target_matrix;
data_tmp = (matrix_multi(1,1) + matrix_multi(2,2) + matrix_multi(3,3) - 1) / 2;
angle = acos(data_tmp);
axis_angle = [(matrix_multi(3,2) - matrix_multi(2,3)) / (2 * sin(angle));
(matrix_multi(1,3) - matrix_multi(3,1)) / (2 * sin(angle));
(matrix_multi(2,1) - matrix_multi(1,2)) / (2 * sin(angle))]; %旋转矢量
end
运行得出的关节位置、速度、加速度曲线如下:
关节位置曲线
关节速度曲线
关节加速度曲线(此处加速度接近0)
可以看出,关节位置连续,但起始与终止处关节速度过渡不平滑,存在刚体冲击,可以考虑附加速度曲线使加速和减速过程平滑过渡。
结论:使用等效轴角坐标系表示姿态进行线性插值实现直线插补的方法除在起始和终止位置处存在刚体冲击外,其插补过程还是比较顺畅的,无明显的抖动现象,当然此外还要注意奇异点问题。
知识有限,以上如有出错的地方,还请见谅指出。