三维向量的简单运算(点积、叉积及点到直线的距离)
点乘比较简单,是相应元素的乘积的和:
V1( x1, y1, z1)·V2(x2, y2, z2) = x1*x2 + y1*y2 + z1*z2;
注意结果不是一个向量,而是一个标量(Scalar)。点乘有什么用呢,我们有:
A·B = |A||B|Cos(θ)
θ是向量A和向量B见夹角。这里|A|我们称为向量A的模(norm)。这样我们就和容易计算两条线的夹角:
Cos(θ) = A·B /(|A|*|B|)
叉乘(cross product)
首先我们知道 ,对于向量u和v, u x v的结果,是得到一个既垂直于u又垂直于v的向量,假设记作n.
则有下面公式
n = u x v;
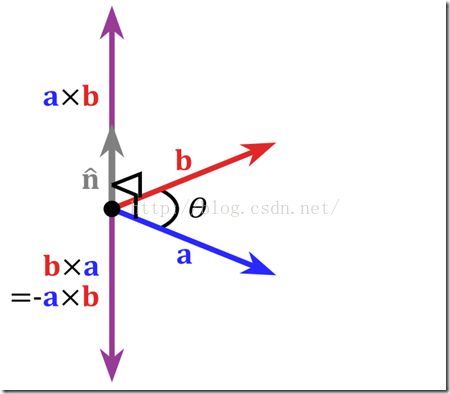
而n的方向,是由右手法则决定的。 即伸出右手,四个手指方向从u绕到v. 此时,大姆指的方向,就是n的方向。 我们通常叫做右向量。
引用一下维基百科的图来说明问题,有兴趣的兄弟可以照图比划一下。 (注:图中向量是用的a x b来表示)
如果只是为了应用的话,走到这一步就可以停下了。后面的知识,只是为了满足一下好奇心。
那我们就来看看,这个结论是怎么来的呢? 我们接着来推导。
为了更好地推导,我们需要加入三个轴对齐的单位向量。
i,j,k.
i,j,k满足以下特点
i = j x k; j = k x i; k = i x j;
k x j = –i; i x k = –j; j x i = –k;
i x i = j x j = k x k = 0; (0是指0向量)
由此可知,i,j,k是三个相互垂直的向量。它们刚好可以构成一个坐标系。
这三个向量的特例就是 i = (1,0,0) j = (0,1,0) k = (0,0,1)。
好,那对于处于i,j,k构成的坐标系中的向量u,v我们可以如下表示
u = Xu*i + Yu*j + Zu*k;
v = Xv*i + Yv*j + Zv*k;
那么 u x v = (Xu*i + Yu*j + Zu*k) x (Xv*i + Yv*j + Zv*k)
= Xu*Xv*(ixi) + Xu*Yv*(i x j) + Xu*Zv*(i x k) + Yu*Xv*(j x i) + Yu*Yv*(j x j) + Yu*Zv*(j x k) + Zu*Xv*( k x i ) + Zu*Yv(k x j) + Zu*Zv(k x k)
由于上面的i,j,k三个向量的特点,所以,最后的结果可以简化为
u x v = (Yu*Zv – Zu*Yv)*i + (Zu*Xv – Xu*Zv)j + (Xu*Yv – Yu*Xv)k;
于是,在i,j,k构成的坐标系中。集就是上面的结果。
当i = (1,0,0) j = (0,1,0) k = (0,0,1)时,我们通常省略i,j,k的写法。最终也就得到了我们的右向量。
叉乘的意义
叉乘表示垂直于uxv的右向量。
使用的地方
可以通过叉乘,修正向量关系,从而构建坐标系。 常见的有 摄相机矩阵和TBN空间转换矩阵的构建。
点到线的距离
找出一个点和一条线间的距离是经常遇见的几何问题之一。假设给出三个点,A,B和C,你想找出点C到点A、B定出的直线间距离。第一步是找出A到B的向量AB和A到C的向量AC,现在我们用该两向量的叉积除以|AB|,这就是我们要找的的距离了(下图中的红线)。
d = (AB x AC)/|AB|
(AB X AC)/2是三角形ABC的面积,这个三角形的底是|AB|,高就是C到AB的距离。有时叉积得到的是一个负值,这种情况下距离就是上述结果的绝对值。
当我们要找点到线段的距离时,情况变得稍稍复杂一些。这时线段与点的最短距离可能是点到线段的某一端点,而不是点到直线的垂线。例如上图中点C到线段AB的最短距离应该是线段BC。我们有集中不同的方法来判断这种特殊情况。第一种情况是计算点积AB Bc来判定两线段间夹角。如果点积大于等于零,那么表示AB到BC是在-90到90度间,也就是说C到AB的垂线在AB外,那么AB上到C距离最近的点就是B。同样,如果BAAC大于等于零,那么点A就是距离C最近的点。如果两者均小于零,那么距离最近的点就在线段AB中的某一点。
点到面的距离
设某三维平面表达式为 a*x+b*y+c*z+d = 0; 则其法向量即为: (a,b,c). 任意一点 p = (x1, y1, z1)到该平面的距离为: (a*x1 + b*y1 + c*z1+d) / (a*a + b*b +c*c)