《神经网络与深度学习》-无监督学习
无监督学习
- 1. 无监督特征学习
- 1.1 主成分分析
- 1.2 稀疏编码
- 1.2.1 训练方法
- 1.2.2 稀疏编码的优点
- 1.3 自编码器
- 1.4 稀疏自编码器
- 1.5 堆叠自编码器
- 1.6 降噪自编码器
- 2. 概率密度估计
- 2.1 参数密度估计
- 2.1.1 正太分布
- 2.1.2 多项分布
- 2.2 非参数密度估计
- 2.2.1 直方图法
- 2.2.2 核方法
- 2.2.3 K近邻方法
无监督学习(Unsupervised Learning,UL)是指从无标签的数据中学习出有用的模式,无监督学习算法一般直接从原始数据中学习,不需要标签。若监督学习是建立输入-输出之间的映射关系,那么无监督学习就是发现隐藏的数据中的有价值信息:有效特征、类别、结构、概率分布等。
主要的几种无监督学习:
-
无监督特征学习(Unsupervised Feature Learning)是从无标签的训练数据中,挖掘有效的特征或表示,无监督特征学习一般用来进行降维、数据可视化、监督学习前期的数据预处理。
-
概率密度估计(Probabilistic Density Estimation)简称密度估计,是根据一组训练样本来估计样本空间的概率密度,密度估计由分为:参数密度估计、非参数密度估计。参数密度估计是建设训练样本服从某个已知概率密度形式的分布(如高斯分布),然后去学习概率密度的参数。非参数密度估计是不假设数据服从某个已知分布,只利用训练样本对密度进行估计,可进行任性形状的密度估计,常见方法有直方图、核密度估计等。
-
聚类(Clustering)是将一组样本数据根据一定的准则划分到不同的组(集群(Cluster))。一个比较通用的准则是组内样本相似度要高于组间样本的相似度。常见的聚类算法:K-Means、谱聚类。
无监督学习方法也包含三个基本要素:模型、学习准则、优化算法。学习准则有最大似然估计、最下重构错误等。
无监督特征学习中,常用学习准则为最小化重构错误、同时也经常对特征进行一些约束:独立性、非负性、稀释性等;
密度估计中,常用学习准则为最大似然估计。
1. 无监督特征学习
无监督特征学习,旨在无标注的数据汇总学习有效数据表示。无监督特征学习主要方法有主成分分析、稀疏编码、自编码器
1.1 主成分分析
主成分分析(Principal Component Analysis,PCA)常用来数据降维,在转换后的空间中数据的方差最大。如图所示二维数据,将数据投影到一维空间中,选择数据方差最大的方向进行投影,能最大化数据差异性,保留更多的原始数据信息。
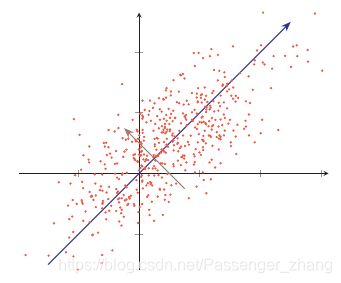
假设一组 D 维的样本 x ∈ R D , 1 ≤ n ≤ N \pmb{x} \in \R^D, 1 \leq n \leq N xxx∈RD,1≤n≤N,将其投影到 1 维空间中,投影向量为 w ∈ R D \pmb{w} \in \R^D www∈RD。不失一般性,我们限制 w \pmb{w} www的模为1,即 w T w = 1 \pmb{w}^T\pmb{w} = 1 wwwTwww=1。每个样本点 x ( n ) \pmb{x}^{(n)} xxx(n) 投影之后的表示为:
z ( n ) = w T x ( n ) z^{(n)} = \pmb{w}^T\pmb{x}^{(n)} z(n)=wwwTxxx(n)
用矩阵 X = [ x ( 1 ) , x ( 2 ) , ⋯ , x ( n ) ] \pmb{X} = [\pmb{x}^{(1)},\pmb{x}^{(2)},\cdots,\pmb{x}^{(n)}] XXX=[xxx(1),xxx(2),⋯,xxx(n)] 表示输入样本, x ‾ = 1 N ∑ n = 1 N x ( n ) \overline{\pmb{x}} = \frac{1}{N}\sum^{N}_{n=1}\pmb{x}^{(n)} xxx=N1∑n=1Nxxx(n)为原来样本的中心点,所有样本投影后的方差为:
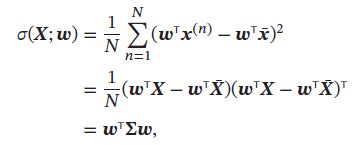
其中 X ‾ = x ‾ 1 D T \overline{X} = \overline{\pmb{x}}1_D^T X=xxx1DT 是向量 x ‾ \overline{\pmb{x}} xxx 和 D 维全1向量 1 D 1_D 1D的外积,即有 D 列 x ‾ \overline{\pmb{x}} xxx 组成的矩阵, ∑ = 1 N ( X − X ‾ ) ( X − X ‾ ) T \sum = \frac{1}{N}(\pmb{X}-\overline{\pmb{X}})(\pmb{X}-\overline{\pmb{X}})^T ∑=N1(XXX−XXX)(XXX−XXX)T 是原始样本的协方差矩阵。
最大化投影方差 σ ( X ; w ) \sigma(\pmb{X};\pmb{w}) σ(XXX;www) 并满足 w T w = 1 \pmb{w}^T\pmb{w} = 1 wwwTwww=1,利用拉格朗日方法转化为无约束优化问题:
max w w T ∑ w + λ ( 1 − w T w ) \max_{w} \pmb{w}^T\sum\pmb{w} + \lambda(1-\pmb{w}^T\pmb{w}) wmaxwwwT∑www+λ(1−wwwTwww)
其中 λ \lambda λ 为拉格朗日乘子。对上式求导并令导数等于0,可得:
∑ w = λ w \sum\pmb{w}=\lambda \pmb{w} ∑www=λwww
从上式可知, w \pmb{w} www是协方差矩阵 ∑ \sum ∑ 的特征向量。同时:
σ ( X ; w ) = w T ∑ w = w T λ w = λ \sigma(\pmb{X};\pmb{w}) = \pmb{w}^T\sum\pmb{w} = \pmb{w}^T \lambda \pmb{w} = \lambda σ(XXX;www)=wwwT∑www=wwwTλwww=λ
λ \lambda λ也是投射后样本的方差,因此,PCA可以转换成一个矩阵特征值分解问题,投影向量 w \pmb{w} www 为矩阵 ∑ \sum ∑ 的最大特征值对应的特征向量。
如果要通过投影矩阵 W ∈ R D × D ′ \pmb{W} \in R^{D\times D^{'}} WWW∈RD×D′ 将样本投到 D ′ D^{'} D′维空间,投影矩阵满足 W T W = I \pmb{W}^T\pmb{W} = \pmb{I} WWWTWWW=III 为单位矩阵,只需要将 ∑ \sum ∑的特征值从大到小排列,保留前 D ′ D^{'} D′个特征向量,对应的特征向量即是最优的投影矩阵:
∑ W = W d i a g ( λ ) \sum \pmb{W} = \pmb{W} diag(\lambda) ∑WWW=WWWdiag(λ)
其中 λ = [ λ 1 , ⋯ , λ D ′ ] \pmb{\lambda} = [\lambda_1, \cdots, \lambda_{D^{'}}] λλλ=[λ1,⋯,λD′] 为S的前 D ′ D^{'} D′ 个最大的特征值。
主成分分析,可作为监督学习的数据预处理方法,用来去噪声并减少特征之间的相关性,但不保证投影后的数据类别可分性更好,提高两类可分性的方法常为监督学习方法,如线性判别分析(Linear Discriminant Analysis,LDA)
1.2 稀疏编码
稀疏编码(Sparse Coding)受哺乳动物视觉系统感受野启发建立的模型。外界信息经过编码后,只有小部分神经元激活,即外界刺激在视觉系统中的表示具有很高的稀疏性。编码的稀疏性在一定程度上符合生物学的低功耗特性。
数学上,(线性)编码是指给定一组基向量 A = [ a 1 , ⋯ , a M ] \pmb{A} = [\pmb{a}_1, \cdots,\pmb{a}_M] AAA=[aaa1,⋯,aaaM],将输入样本 x ∈ R D \pmb{x} \in \R^D xxx∈RD表示为这些基向量的线性组合:

其中基向量的系数 z = [ z 1 , ⋯ , z M ] \pmb{z} = [\pmb{z}_1,\cdots,\pmb{z}_M] zzz=[zzz1,⋯,zzzM] 输入样本的编码(Encoding),基向量 A \pmb{A} AAA 也称为子典(Dictionary).
编码是对 D D D 维空间中的样本 x \pmb{x} xxx 找到其在 P 维空间中的表示(或投影),其目标通常是编码的各个维度都是独立统计的,并且可以重构出输入样本。编码的关键是找到一组“完备”的基向量 A \pmb{A} AAA ,比如主成分分析,但PCA得到的编码通常是稠密的

为得到稀疏编码,需找到一组“过完备”的基向量(M>D)来进行编码,在过完备基向量之间常会存在一些冗余性,因此对一个输入样本,会存在很多有效的编码,如果加上稀疏性限制,可以减少解空间的大小,得到“唯一”的稀疏编码。
给定一组N个输入 [ x ( 1 ) , ⋯ , x ( N ) ] [\pmb{x}^{(1)}, \cdots,\pmb{x}^{(N)}] [xxx(1),⋯,xxx(N)] ,其稀疏编码的目标函数定义为:

其中 Z = [ z ( 1 ) , ⋯ , z ( N ) ] \pmb{Z} = [z^{(1)}, \cdots, z^{(N)}] ZZZ=[z(1),⋯,z(N)] , ρ ( ⋅ ) \rho(\cdot) ρ(⋅) 是一个稀疏性衡量函数, η \eta η是超参数,用来控制稀疏性的强度。
对于一个给定的 z ∈ R M z \in \R^M z∈RM,其稀疏性定义为非零元素的比例。如果一个向量只有很少的几个非零元素,就说该向量稀疏。稀疏性衡量函数 ρ ( z ) \rho(\pmb{z}) ρ(zzz) 是给向量 z \pmb{z} zzz一个标量分数, z \pmb{z} zzz越稀疏, ρ ( z ) \rho(\pmb{z}) ρ(zzz)越小。
稀疏性衡量函数的多种选择,如 l 0 l_0 l0 范数:
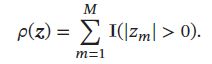
l 0 l_0 l0 范数不满足连续可导,很难优化,实际中,稀疏性衡量函数常为 l 1 l_1 l1范数:

稀疏性衡量函数或为对数函数:
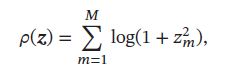
1.2.1 训练方法
给定一组 N 个输入向量 { x ( n ) } n = 1 N \{\pmb{x}^{(n)}\}_{n=1}^{N} {xxx(n)}n=1N ,需要同时学习基向量 A \pmb{A} AAA 以及每个输入样本对应的稀疏编码 { z ( n ) } n = 1 N \{\pmb{z}^{(n)}\}_{n=1}^{N} {zzz(n)}n=1N
稀疏编码的训练过程一般用交替优化的方法进行:
- 固定基向量 A \pmb{A} AAA ,对每个输入 x ( n ) \pmb{x}^{(n)} xxx(n),计算其对应的最优编码:
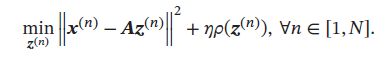
- 固定上一步得到的编码 { z ( n ) } n = 1 N \{\pmb{z}^{(n)}\}_{n=1}^{N} {zzz(n)}n=1N,计算其最优的基向量:
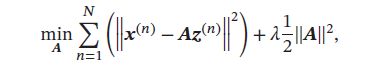
其中第二项为正则化项, λ \lambda λ为正则化项系数。
1.2.2 稀疏编码的优点
稀疏编码的每一维都可以看做是一种特征,和基于稠密向量的分布式表示比,稀疏编码计算量小、可解释性强。
计算量 稀疏性可以极大地降低计算量
可解释性 稀疏编码只有少量非零元素,相当于每一个输入样本表示为少数几个相关的特征,可更好地描述其特征,并易于理解。
特征选择 稀疏性可实现特征的自动选择,只选择和输入样本最相关的少数特征,从而更高效地表示输入样本,降低噪声,减轻过拟合。
1.3 自编码器
自编码器(Auto-Encoder,AE)是通过无监督的方式来学习一组数据的有效编码(或表示)。
假设有一组D维的样本 x ( n ) ∈ R D , 1 ≤ n ≤ N \pmb{x}^{(n)} \in \R^D,1 \leq n \leq N xxx(n)∈RD,1≤n≤N,自编码器将其映射到特征空间得到每个样本的编码 x ( n ) ∈ R M , 1 ≤ n ≤ N \pmb{x}^{(n)} \in \R^M,1 \leq n \leq N xxx(n)∈RM,1≤n≤N,并希望这组编码可重构出原来的样本。
自编码器的机构可分为两部分:
- 编码器(Encoder): f : R D → R M f:\R^D \to \R^M f:RD→RM
- 解码器(Decoder): f : R M → R D f:\R^M \to \R^D f:RM→RD
自编码器的学习目标是最小化重构错误(Reconstruction Error):
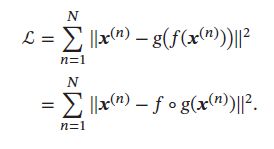
如果特征空间的维度M小于原始空间维度D,自编码器相当于是一种降维或特征抽取方法,如果 M > D M > D M>D,则可找到一组或多组解使得 f ∘ g f \circ g f∘g 为单位函数(Identity Function),并使得重构错误为0,但这样的解无意义。但如果加上附加约束,则有意义,如编码的稀疏性、取值范围、 f f f 和 g g g 的具体形式等。我们可以让编码只取K个不同的值(K
最简单的自编码器如图所示两层神经网络,输入层到隐藏层用来编码,隐藏层到输出层用来解码,层与层之间互相连接:

对于样本 x \pmb{x} xxx,自编码器的中间隐藏层的活性值为 x \pmb{x} xxx 的编码,即:
![]()
自编码器的输出为重构的数据:
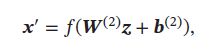
其中 W ( 1 ) , W ( 2 ) , b ( 1 ) , b ( 2 ) \pmb{W}^{(1)},\pmb{W}^{(2)},\pmb{b}^{(1)},\pmb{b}^{(2)} WWW(1),WWW(2),bbb(1),bbb(2) 是网络参数, f ( ⋅ ) f(\cdot) f(⋅)为激活函数,如果令 W ( 2 ) = W ( 1 ) T \pmb{W}^{(2)}=\pmb{W}^{(1)^T} WWW(2)=WWW(1)T,则称为捆绑权重(Tied Weight)。捆绑权重自编码器的参数更少,因此更容易学习。此外,捆绑权重还在一定程度上起到正则化的作用。
对于样本 x ( n ) ∈ [ 0 , 1 ] D , 1 ≤ n ≤ N \pmb{x}^{(n)} \in [0,1]^D, 1 \leq n \leq N xxx(n)∈[0,1]D,1≤n≤N,其重构错误为:

通过最小化重构错误,可以有效地学习网络的参数。
使用自编码器是为了得到有效的数据表示,训练结束后,一般去掉解码器,只保留编码器,编码器的输出可直接作为后续机器学习模型的输入。
1.4 稀疏自编码器
自编码器既能学习低维编码,也能学习高维稀疏编码,假设中间隐藏层 z \pmb{z} zzz 的维度 M 大于输入样本 x \pmb{x} xxx 的维度 D ,并让 z \pmb{z} zzz 尽量稀疏,这就是稀疏自编码(Sparse Auto-Encoder)。类似稀疏编码,稀疏自编码可解释性高,进行了隐式特征选择。
通过给自编码器隐藏层单元 z \pmb{z} zzz 加上稀疏性限制,自编码器可以学习到数据中一些有用的结构。给定 N 个训练样本 { x ( n ) } n = 1 N \{\pmb{x}^{(n)}\}_{n=1}^{N} {xxx(n)}n=1N,稀疏自编码器的目标函数为:
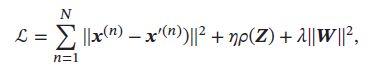
其中 Z = [ z ( 1 ) 、 ⋯ 、 z ( N ) ] \pmb{Z} = [\pmb{z}^{(1)}、\cdots、\pmb{z}^{(N)}] ZZZ=[zzz(1)、⋯、zzz(N)]表示所有训练样本的编码, ρ ( Z ) \rho(Z) ρ(Z) 为稀疏性度量函数, W \pmb{W} WWW表示自编码器中的参数。
稀疏性度量函数 ρ ( Z ) \rho(Z) ρ(Z) 分别计算每个编码 z ( n ) \pmb{z}^{(n)} zzz(n)的稀疏度,再进行求和,此外, ρ ( Z ) \rho(Z) ρ(Z) 还可以定义为一组训练样本中每一个神经元激活的概率。
其中 ρ j ^ \hat{\rho_j} ρj^ 可近似看做是第 j 个神经元激活的概率,我们希望 ρ j ^ \hat{\rho_j} ρj^ 接近于一个事先给定的值 ρ ∗ \rho^* ρ∗,如0.05,可以通过KL距离来衡量 ρ j ^ \hat{\rho_j} ρj^ 与 ρ ∗ \rho^* ρ∗ 的差异:

如果 ρ j ^ = ρ ∗ \hat{\rho_j} = \rho^* ρj^=ρ∗ ,则 K L ( ρ ∗ ∣ ∣ ρ j ^ ) = 0 KL( \rho^*||\hat{\rho_j}) = 0 KL(ρ∗∣∣ρj^)=0
稀疏性度量函数定义为:
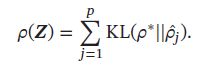
1.5 堆叠自编码器
对很多数据来说,两层神经网络的自编码器不足以获取好的数据表示,因此,可以更深的网络,这样提取的数据表示更抽象,能很好捕捉到数据的语义信息。实践中,常用逐层堆叠的方式来训练一个深层的自编码器,称为堆叠自编码器(Stacked Auto-Encoder,SAE),常采用逐层训练(Layer-Wise Training)来学习网络参数。
1.6 降噪自编码器
有效的数据表示除最小重构错误、稀疏性,有时还要具备对数据部分损坏(Partial Destruction)的鲁棒性,高维数据(比如图像)一般都具有信息冗余,如常可根据一张部分损坏的图像联想出完整内容,故也希望自编码器也能够从损坏的数据中得到有效的数据表示,并能恢复出完整的原始信息。
降噪自编码器(Denoising Auto-Encoder)是通过引入噪声来增加编码鲁棒性的自编码器,并能提高模型泛化能力。对于一向量 x \pmb{x} xxx,我们首先根据一比例 μ \mu μ随机将 x \pmb{x} xxx的一些维度的值设为0,得到一个被损坏的向量 x ~ \tilde{x} x~,然后将被损坏的向量 x ~ \tilde{x} x~输入给自编码器得到编码 z \pmb{z} zzz,并重构出原始的无损输入 x \pmb{x} xxx。
自编码器与降噪编码器的对比如下, f θ f_{\theta} fθ 为编码器, g θ ′ g_{\theta^{'}} gθ′ 为解码器, L ( x , x ′ ) L(\pmb{x}, \pmb{x}^{'}) L(xxx,xxx′) 为重构错误:

2. 概率密度估计
概率密度估计(Probabilistic Density Estimation),简称密度估计(Density Estimation),基于一些观测样本来估计一个随机变量的概率密度函数。密度估计方法分为:参数密度估计、非参数密度估计
2.1 参数密度估计
参数密度估计(Parametric Density Estimation)根据先验知识假设随机变量服从某种分布,然后通过训练样本来估计分布的参数。
令 D = { x ( n ) } n = 1 N D=\{\pmb{x}^{(n)}\}_{n=1}^N D={xxx(n)}n=1N为从某个未知分布中独立抽取的N个训练样本,假设这些赝本服从一个概率分布函数 p ( x ; θ ) p(\pmb{x};\theta) p(xxx;θ),其对应似然函数为:
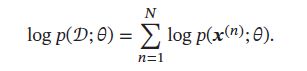
我们要估计一个参数 θ M L \theta^{ML} θML 来使得:

这样参数估计问题转化为最优化问题。
2.1.1 正太分布
假设样本 x ∈ R D \pmb{x} \in \R^D xxx∈RD 服从正太分布:
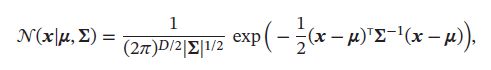
其中 μ \mu μ和 ∑ \pmb{\sum} ∑∑∑ 是均值和方差。
数据集 D = { x ( n ) } n = 1 N D=\{\pmb{x}^{(n)}\}_{n=1}^N D={xxx(n)}n=1N的对数似然函数为:

分别求上式关于 μ \mu μ和 ∑ \pmb{\sum} ∑∑∑ 的偏导数,并令其等于 0,可得到:

2.1.2 多项分布
假设样本服从K个状态的多项分布,令one-hot向量 x ∈ { 0 , 1 } K \pmb{x} \in \{0,1\}^K xxx∈{0,1}K来表示第k个状态,即 x k = 1 x_k=1 xk=1,其余 x i = 0 , i ≠ k x_{i}=0,i\not=k xi=0,i=k。样本 x \pmb{x} xxx 的概率密度函数为:
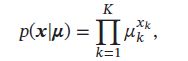
其中 μ k \mu_k μk 为第 k 个状态的概率,并满足 ∑ k = 1 K μ k = 1 \sum_{k=1}^{K}\mu_k=1 ∑k=1Kμk=1.
数据集 D = { x ( n ) } n = 1 N D=\{\pmb{x}^{(n)}\}_{n=1}^N D={xxx(n)}n=1N的对数似然函数为:
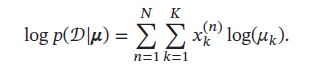
多项分布的参数估计为约束优化问题,引入拉格朗日乘子 λ \lambda λ,将原问题转换为无约束优化问题:

分别求上式关于 μ k \mu_k μk, λ \lambda λ的偏导数,并令其等于0,可得到:

其中 m k = ∑ n = 1 N x k ( n ) m_k = \sum_{n=1}^{N}x_k^{(n)} mk=∑n=1Nxk(n) 为数据集汇总取值为第k个状态的样本数量。
参数密度估计存在的问题:
- 模型选择问题:即如何选择数据分布的密度函数,实际数据的分布复杂,不是简单的正太分布或多项分布。
- 不可观测变量问题:即用来训练的样本只包含部分的可观测变量,有一些关键的变量无法预测,这导致很难准确估计数据的真实分布。
- 维度灾难问题:高维数据的参数估计十分困难,随维度增加,估计参数所需的样本数量指数增加,样本不足时,出现过拟合。
2.2 非参数密度估计
非参数密度估计(Nonparametric Density Estimation)不事先假设数据的分布,通过将样本空间会分为不同的区域并估计每个区域的概率,来近似数据的概率密度函数。
对于高维空间的随机变量 x \pmb{x} xxx,假设其服从一个未知分布 p ( x ) p(x) p(x),则 x \pmb{x} xxx落在空间中的小区域R的概率:

给定N个训练样本, D = { x ( n ) } n = 1 N D=\{\pmb{x}^{(n)}\}_{n=1}^N D={xxx(n)}n=1N,落入区域R的样本数量K服从二项分布:
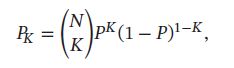
其中 K/N 的期望为 P, 方差为 v a r ( K / N ) = P ( 1 − P ) / N var(K/N)=P(1-P)/N var(K/N)=P(1−P)/N 当N非常大时,我们可以近似认为:
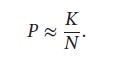
假设区域R足够小,其内部的概率密度相同,则有:
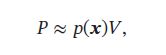
其中 V 为区域 R 的体积,结合上述公式,得到:

要准确估计 p ( x ) p(\pmb{x}) p(xxx),需尽量使用样本数量N足够大,区域体积V尽可能小,实际中,样本数量有限,过小区域会导致落入该区域的样本比较少,这样估计的概率密度不太准确,故实践中,非参数密度估计有两种方式:
- 固定区域大小V,统计落入不同区域的数量,这种方式包括直方图方法和核方法
- 改变区域大小V,使落入每个区域的样本数量为K,这种方式为K近邻方法。
2.2.1 直方图法
直方图方法(Histogram Method)是直观的估计连续变量密度函数的方法,可表示为一种柱状图。
以一维随机变量为例,首先将取值范围分为 M 个连续的、不重叠的区间,每个区间宽度为 Δ m \Delta_m Δm。对于给定的训练样本 D = { x ( n ) } n = 1 N D=\{\pmb{x}^{(n)}\}_{n=1}^N D={xxx(n)}n=1N,统计这些样本落入每个区间的数量 K m K_m Km,然后将它们归一化为密度函数:
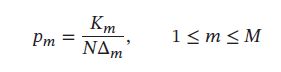
其中区间宽度 Δ m \Delta_m Δm常设为相同的值 Δ \Delta Δ,直方图方法的关键问题是如何选择一个合适的区间宽度 Δ \Delta Δ,如果 Δ \Delta Δ太小,落入每个区间的样本数量会比较少,其估计的区间密度也有很大的随机性;如果 Δ \Delta Δ太大,其估计的密度函数将变得十分平滑,很难反映真实数据分布。图示如下:蓝线表示真实的密度函数、红色的柱状图为估计的密度。

直方图难以用来处理低维变量,可以很快速地对数据的分布进行可视化,但很难拓展到高维变量。假设一个D维随机变量,如果每一维都划分为M个区间,那么整个空间的区间数量为 M D M^D MD个,直方图方法需要的样本数量会随着维度D的增加而指数增长,从而导致维度灾难。
2.2.2 核方法
核密度估计(Kernel Density Estimation),也叫Parzen 窗方法,是一种直方图方法的改进。
假设R为D维空间中的一个以点 x 为中心的“超立方体”,并定义核函数:

来表示一个样本 z \pmb{z} zzz 是否落入该超立方体中,其中 H 为超立方体边长,也叫核函数的宽度。
给定的训练样本 D = { x ( n ) } n = 1 N D=\{\pmb{x}^{(n)}\}_{n=1}^N D={xxx(n)}n=1N,落入区域 R 的样本数量 K 为:
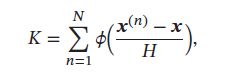
则点 x 的密度估计为:

其中 H D H^D HD 表示超立方体R的体积。
除超立方体核函数,还可以选择更平滑的核函数,如高斯核函数:

其中 h 2 h^2 h2 可看做是高斯核函数的方差,这样,点x的密度估计为:
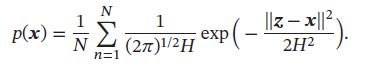
核密度估计方法中的核宽度是固定的,因此同一个宽度可能对高密度的区域过大,而对低密度的区域过小。
2.2.3 K近邻方法
设置可变宽度的区域,并使落入每个区域中样本数量为固定的K,要估计x的密度,先找到一个以x为中心的球体,使得落入球体的样本数量为 K ,根据 p ( x ) ≈ K N V p(x) \approx \frac{K}{NV} p(x)≈NVK 可计算点x的密度,因为落入球体的样本也是离x最近的K个样本,故此方法称为 K近邻方法(K-Nearest Neighbor)。
KNN中,K的选择很关键,K太小,无法有效估计密度函数;K太大,也会使得局部的估计不准确,增加计算开销。
KNN常用于分类,K=1时,为最近邻分类器,最近邻分类器的一个性质是,当 N → ∞ N \to \infty N→∞时,其分类错误率不超过最优分类器错误率的两倍。

