【数论】Pollard-Rho 算法总结

Pollard-Rho 算法总结

预备知识

1. 质因数分解；
2. 生日悖论。

然后就愉快的开始吧。

Part.I 如何对一个大合数进行质因数分解

设有一个大合数$N=p\times q,(p\ne q)$，那么我们可以用什么方法去把它分成两个数的乘积呢？

显然我们可以只找到$p$或者$q$，另一个用$N$去除一下就好了。

那么如何去找这个数？显然可以用暴力方法去找 (代码过于简单就不给了)。

显然这是要爆炸的。。。

Part.II 随机化？？？

考虑随机数？？？

显然这个复杂度瞬间达到了$O($玄学$)$。

但是这就是Pollard-Rho算法的可行基础。。。

Part.III 生日悖论？？？

先看一下这个问题

考虑从$[1,1000]$中选出一个数，要求恰好是$42$，显然这个概率为$\frac{1}{1000}$。

那么我们要选两个数$i,j$使得$i-j=42$呢？算一下就可以发现这个概率大概是$\frac{1}{500}$。

那么我们要选出$k$个数$x_1,x_2,\dots ,x_k$使得$x_i-x_j=42$呢？

写个程序玩一下就会发现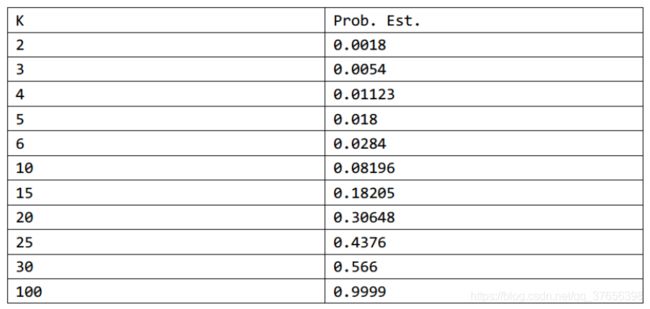：选了100个数的概率居然非常接近$1$了。

这个被称为生日悖论

Part.IV 如何用生日悖论

多打打表就发现当我们选取$k=\sqrt{N}$个数时，成功的概率已经超过了$50\%$。

换句话说，我们已经将找到质因数的概率从$\frac{1}{N}$提到了$\sqrt{\frac{1}{N}}$。这意味着我们对于一个$10^{10}$级别的数，我们只需找到$k=10^5$个数。

但是，另一个不幸的消息是我们需要用$k^2$次除法和比较。 这不是又炸了QAQ…

然而我们可以这样来做：对于一个$x_i$，再随机构造一个$x_y$，求$\gcd (|x_i-x_y|,N)$，可以发现，当这个$\gcd (|x_i-x_y|,N)$不等于$1$时，我们就找到了一个质因子。

但直接存下这$k$个数似乎不太可能存进去。

Part.V 总算到了Pollard-Rho算法

Pollard-Rho算法的实现只存下了两个数。

我们一直往下生成两个数，每次只比较和检查这两个数，然后直到找到我们想要的数。

我们使用一个伪随机数算法来生成下一个数，设当前数数$x$，则我们的下一个数就是$x^2+a\mathrm{m}\mathrm{o}\mathrm{d}N$。

P.S.关于常数$a$，可以指定，也可以rand()一个。

Part.VI 还有问题？？？

如果你运气好的话，你总会遇到一些数，他们会让Pollard-Rho算法进入死循环。

如何解决？

有一种方法是开一个数组，然后不断标记。

然而数字很大的时候就要炸。。。

考虑这样一个问题：

你在操场上走，然而操场周围的景物都一样，那么你如何知道你已经走了一圈？

一个有效的方法是再找一个人 不要问我怎么找到的 ，然后让他以你的两倍的速度向前走，当你和那个人相遇时，你就走完了一圈。

这样的话，我们就可以用两个变量$x,y$，初始值相同，每次进入循环时，令$x=f(x),y=f(f(y))$，每次只需检查$\gcd (|x-y|,N)$即可。

模版

typedef long long ll;
const int pri[]={2,3,5,7,11,13,17,19,23,29};

inline ll QuickMul(ll a,ll b,ll mod) {
	a%=mod,b%=mod;
	ll ret=0;
	while(b) {
		if(b&1)ret=(ret+a)%mod;
		a=(a+a)%mod;
		b>>=1;
	}
	return ret;
}
inline ll GCD(ll x,ll y) {return y==0?x:GCD(y,x%y);}
inline ll ABS(ll x) {return x<0?-x:x;}

ll PollardRho(ll n) {
	for(int i=0;i<10;i++)
		if(n%pri[i]==0)return pri[i];
	ll x=(1LL*rand()*rand()%(n-2))+2;
	ll y=x;
	ll c=(1LL*rand()*rand()%(n-1))+1;
	ll d=1;
	while(d==1) {
		x=(QuickMul(x,x,n)+c+n)%n;
		y=(QuickMul(y,y,n)+c+n)%n;
		y=(QuickMul(y,y,n)+c+n)%n;
		d=GCD(ABS(x-y),n);
		if(d==n)return n;
	}
	return d;
}