红黑树(C语言实现)

红黑树的性质

• 每个结点是红的或者黑的
• 根结点是黑的
• 每个叶子结点是黑的
• 如果一个结点是红的，则它的两个儿子都是黑的
• 对每个结点，从该结点到其子孙结点的所有路径上的包含相同数目的黑结点

红黑树的定义

#define RED   1
#define BLACK 2
//红黑树的节点
typedef struct _rbtree_node
{
	int color;
	struct _rbtree_node *parent;
	struct _rbtree_node *left;
	struct _rbtree_node *right;

	int key;
	void *value;
}rbtree_node;
//红黑树 	nil为叶子节点
typedef struct _rbtree
{
	struct _rbtree_node *root;
	struct _rbtree_node *nil;
}rbtree;

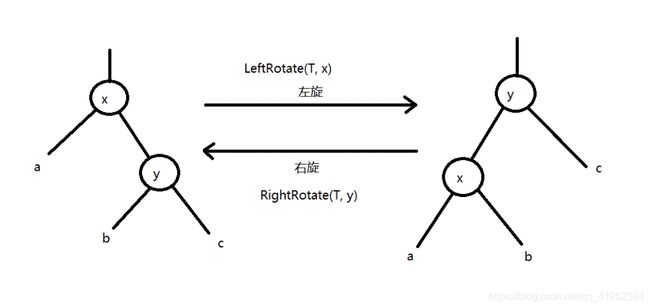
左旋和右旋

int rbtree_left_rotate(rbtree *root,rbtree_node *x)
{
	if( root == NULL || x ==  NULL) return -1;

	rbtree_node *y = x->right;

	x->right = y->left;
	if(y->left != root->nil){
		y->left->parent = x;
	}

	y->parent = x->parent;
	if(x->parent == root->nil){
		root->root = y;
	}else if(x->parent->left == x){
		x->parent->left = y;
	}else{
		x->parent->right = y;
	}

	y->left = x;
	x->parent = y;

	return 0;
}
//写完一个旋转之后，只要把left改成right，把right改成left就行
int rbtree_right_rotate(rbtree *root,rbtree_node *x)
{
	if( root == NULL || x ==  NULL) return -1;
	
	rbtree_node *y = x->left;

	x->left = y->right;
	if(y->right != root->nil){
		y->right->parent = x;
	}

	y->parent = x->parent;
	if(x->parent == root->nil){
		root->root = y;
	}else if(x->parent->left == x){
		x->parent->left = y;
	}else{
		x->parent->right = y;
	}

	y->right = x;
	x->parent = y;

	return 0;
}

红黑树的插入

• 插入方式和二叉搜索树的方式一样，然后调整

• 插入节点的颜色为红色。为什么这么做?

  ​ 红黑树的性质5，也就是“该结点到其子孙结点的所有路径上的包含相同数目的黑结点”，如果增加一个红色的节点红黑树的这个一个性质不会变

• 什么时候需要调整?

  ​ 当插入节点的父节点是红色的时候需要调整。因为插入节点是红色不会违背性质5，但是如果父节点是红色就违背的性质4，也就是"如果一个结点是红的，则它的两个儿子都是黑的"

需要调整插入情况分析(也就是父节点时红色的情况)

• 插入时叔父节点(父亲的兄弟)是黑色

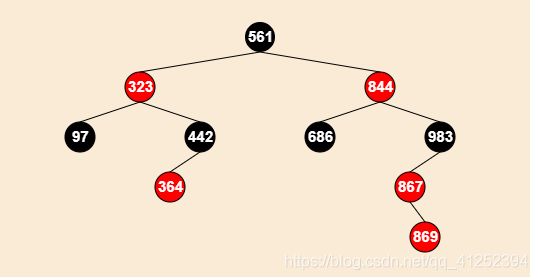
插入869节点：如果叔父节点是黑色，那么叔父节点就是一个叶子节点，为什么?

红黑树的性质5，也就是"该结点到其子孙结点的所有路径上的包含相同数目的黑结点"。是以任何红黑树的一个节点为根节点都是成立的(当前例子以983节点为根)。在没有插入869之前是满足性质5的，假如右节点不是叶子节点，那么黑色节点数量就是3，左边是2，不满足性质5。所以可以反推出叔父节点为黑色是叶子节点。这种情况在节点插入之前明显是红色那一方更深。

• 插入时叔父节点是红色

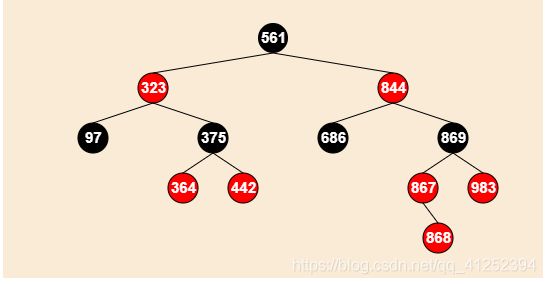
插入868节点：如果叔父节点是红色，那么叔父两个儿子是叶子节点，为什么?

红黑树的性质5，也就是"该结点到其子孙结点的所有路径上的包含相同数目的黑结点"。和上面一样以869为根算黑节点数量(没有插入868节点时的情况)。假设叔父节点两儿子不是叶子节点，那么必须是黑节点，如果是黑节点那么性质5就不满足了。这种情况在节点插入之前两边的高度是一样的。

上述情况的调整方法

• 插入时叔父节点是红色(插入868)

1 将“父节点”设为黑色

2 将“叔叔节点”设为黑色

3 将“祖父节点”设为“红色

4 将“祖父节点”设为“当前节点”，之后继续对“当前节点”进行操作(也就是继续对以869为节点继续调整，如果父节点时红色继续调整，不是就不需要，这种情况是需要的。)

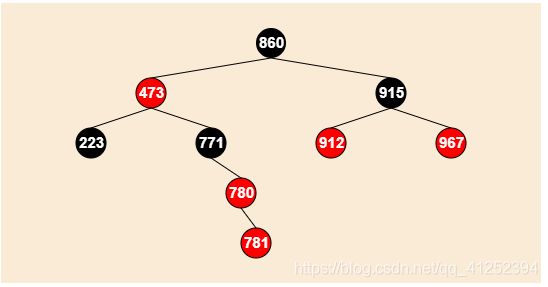
• 插入时叔父节点时黑色(插入781)。

  ​ 情况1(父节点和子节点都是同一方向的节点，当前是父节点是祖父的右节点，插入节点是父节点的右节点。)

1 将“父节点”设为“黑色”

2 将“祖父节点”设为“红色”

3 以“祖父节点”为支点进行左旋(如果是对称情况就是右旋–>父节点是祖父的左节点，插入节点是父节点的左节点)

情况2(父节点和子节点不是同一方向的节点，当前是父节点是祖父节点的右节点，插入节点是父节点的左节点)

1 将“父节点”作为“新的当前节点”
2 以“新的当前节点”为支点进行右旋(这个也是有对称情况的)

旋转完成之后的情况

3 此时情况和情况1是一样的

插入的具体代码

int rbtree_insert_fixup(rbtree *root,rbtree_node *newnode)
{
	if(root == NULL || newnode == NULL) return -1;

	rbtree_node *it = newnode;
	while( it->parent->color == RED ){//插入节点的父亲是红色才调整
		if( it->parent->parent->left == it->parent ){//判断父节点是祖父节点的left还是right
			rbtree_node *uncle = it->parent->parent->right;//叔父节点
			
			if( uncle->color == RED ){//叔父节点是红色
				
				uncle->color = BLACK;
				it->parent->color = BLACK;
				uncle->parent->color = RED;
				it = it->parent->parent;
				
			}else{//叔父节点是黑色
				//情况2-->父节点和子节点不是同一方向的节点。调整完成后变成情况1
				if( it->parent->right == it ){
					it = it->parent;
					rbtree_left_rotate(root, it);
				}
				//情况1-->父节点和子节点都是同一方向的节点
				it->parent->color = BLACK;
				it->parent->parent->color = RED;
				rbtree_right_rotate(root, it->parent->parent);
			}
		}else{//对称情况，和左旋右旋一样，把left改成right，把right改成left
			rbtree_node *uncle = it->parent->parent->left;
			
			if( uncle->color == RED ){
				
				uncle->color = BLACK;
				it->parent->color = BLACK;
				uncle->parent->color = RED;
				it = it->parent->parent;
				
			}else{

				if( it->parent->left == it ){
					it = it->parent;
					rbtree_right_rotate(root, it);
				}

				it->parent->color = BLACK;
				it->parent->parent->color = RED;
				rbtree_left_rotate(root, it->parent->parent);
			}
		}

	}

	root->root->color = BLACK;//根节点始终是黑色

	return 0;
}

int rbtree_insert(rbtree *root,rbtree_node *newnode)
{
	if(root == NULL || newnode == NULL) return -1;

	rbtree_node * it = root->root;
	rbtree_node * y = it;//y是用来缓存上一次的节点
	//查找到新节点的插入位置
	while(it != root->nil){
		y = it;
		if(it->key > newnode->key){
			it = it->left;
		}else if(it->key < newnode->key){
			it = it->right;
		}else{
			return -2;
		}
	}
	//插入节点
	if( y == root->nil ){//第一次插入
		root->root = newnode;
	}if(y->key > newnode->key){
		y->left = newnode;
	}else{
		y->right = newnode;
	}
	//初始化节点
	newnode->parent = y;
	newnode->color = RED;
	newnode->left = root->nil;
	newnode->right = root->nil;
	//调整
	rbtree_insert_fixup(root,newnode);

	return 0;
}

红黑树的删除

• 删除方式和二叉搜索树的方式一样，然后调整

• 什么时候需要调整?

  当删除节点的颜色是黑色时调整，少一个黑色节点意味着性质5是肯定不会成立的

删除的情况和调整方法

• 兄弟节点是红色的(删除29)

1 将x的兄弟节点设为“黑色”。
2 将x的父节点设为“红色”。
3 对x的父节点进行左旋。
4 左旋后，重新设置x的兄弟节点。

• 兄弟节点是黑色的(删除87)

  情况1(兄弟节点的两儿子是黑色的)

1 将被删节点的兄弟节点设为“红色”。
2 设置“被删节点的父节点”为“新的被删节点节点”。

• 兄弟节点是黑色的(删除595)

  情况2(有一个儿子是红色的，并且兄弟节点的为父节点的右节点，兄弟节点的儿子也为兄弟节点的右节点(同方向)，此时不用管另一个儿子的颜色)

1 将被删节点父节点颜色 赋值给 被删节点的兄弟节点。
2 将被删节点父节点设为“黑色”。
3 将被删节点兄弟节点的右子节点设为“黑色”。
4 对被删节点的父节点进行左旋。
5 设置“被删节点”为“根节点”。

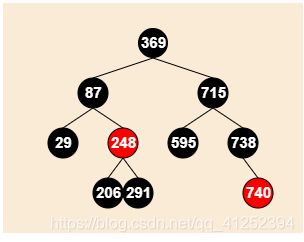
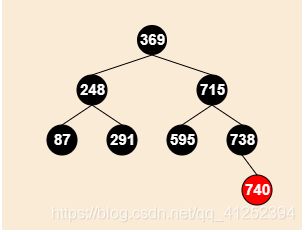
• 兄弟节点是黑色的(删除291)
  情况3(有一个儿子是红色的，并且兄弟节点的为父节点的左节点，兄弟节点的儿子为兄弟节点的右节点(不同方向))
  

  1 将被删节点兄弟节点的右孩子设为“黑色”。

  2 将被删节点兄弟节点设为“红色”。

  3 对被删节点的兄弟节点进行左旋。

  4 左旋后，重新设置被删节点的兄弟节点

  -

  5 此时变成了情况2

删除代码的实现

int rbtree_delete_fixup(rbtree *root, rbtree_node *node) 
{
	if(root == NULL || node == NULL) return -1;
	
	while((node != root->root) && (node->color == BLACK)){

		if(node == node->parent->right){

			rbtree_node *brother = node->parent->left;//兄弟节点
			if(brother->color == RED){//兄弟节点是红色
				brother->parent->color = RED;
				brother->color = BLACK;
				rbtree_right_rotate(root, brother->parent);
				brother = node->parent->left;
            //下面是兄弟节点是黑色的情况。。。情况1兄弟节点两个儿子是黑色
			}else if(brother->left->color == BLACK && brother->right->color == BLACK){
				brother->color = RED;
				node = node->parent;
			}else{
                //儿子全黑判断完了意味着至少有一个红，如果左边是黑色的，那么右边必须是红色，就是情况2
				if(brother->left->color == BLACK){
					brother->right->color = BLACK;
					brother->color = RED;
					rbtree_left_rotate(root, brother);
					brother = node->parent->left;
				}
				//情况3，有可能是两个儿子节点都是红色的，也有可能左边是红色右边是黑色
				brother->color = brother->parent->color;
				brother->parent->color = BLACK;
				brother->left->color = BLACK;
				rbtree_right_rotate(root, brother->parent);
				node = root->root;
			}

		}else{//对称情况
			rbtree_node *brother = node->parent->right;
			if(brother->color == RED){
				brother->parent->color = RED;
				brother->color = BLACK;
				rbtree_left_rotate(root, brother->parent);
				brother = node->parent->right;
			}else if(brother->left->color == BLACK && brother->right->color == BLACK){
				brother->color = RED;
				node = node->parent;
			}else{
				if(brother->right->color == BLACK){
					brother->left->color = BLACK;
					brother->color = RED;
					rbtree_right_rotate(root, brother);
					brother = node->parent->right;
				}
				
				brother->color = brother->parent->color;
				brother->parent->color = BLACK;
				brother->right->color = BLACK;
				rbtree_left_rotate(root, brother->parent);
				node = root->root;
			}
		}

	}

	node->color = BLACK;

	return 0;
}

int rbtree_replace(rbtree *root,rbtree_node *x,rbtree_node *y)
{
	if(root == NULL || root->root == root->nil) return -1;

	if( x == NULL || x == root->nil ) return -2;
	
	rbtree_node *p = x->parent;
	if( p == root->nil ){
		root->root = y;
	}else if( p->left == x){
		p->left = y;
	}else{
		p->right = y;
	}

	y->parent = p;

	return 0;
}

int rbtree_delete(rbtree *root,rbtree_node *node)
{

	if(root == NULL || node == NULL) return -1;

	rbtree_node *x = root->nil;//替换节点
	rbtree_node *y = root->nil;//y是正真删除的节点
	//如果删除的节点只有一个节点，那么删除节点就是node
	if(node->right == root->nil || node->left == root->nil){
		y = node;
	}else{//删除节点有两个节点，找替换节点，该节点的右子树的最小值
		y = rbtree_min(root, node->right);
	}
	//x是y的替换节点如果没有节点就是nil
	if(y->right != root->nil){
		x = y->right;
	}else if(y->left != root->nil){
		x = y->left;
	}

	rbtree_replace(root,y,x);

	if(y != node){
		node->key = y->key;
		node->value = y->value;
	}
	//删除节点是黑色的才调整
	if(y->color == BLACK){
		rbtree_delete_fixup(root, x);
	}

	return 0;
}