无约束优化——梯度下降法
有 d d d元函数 f ( x ⃗ ) f(\vec{x}) f(x),其中 x ⃗ \vec{x} x为 d d d维向量,试图找到 x ⃗ \vec{x} x的某个取值 x ⃗ ∗ \vec{x}^* x∗,使 f ( x ⃗ ∗ ) f(\vec{x}^*) f(x∗)达到 f ( x ⃗ ) f(\vec{x}) f(x)的最小值(或最大值),这就是我们常说的“最优化”或“优化”。我们知道,机器学习中用训练集训练模型,其实大多时候就是建立目标函数,找到使目标函数达到最小值(或最大值)的模型参数的过程。这不就是在解决优化问题吗!所以,学好优化,刻不容缓!
如果函数 f ( x ⃗ ) f(\vec{x}) f(x)没有附带约束条件,那这属于无约束优化;如果函数 f ( x ⃗ ) f(\vec{x}) f(x)附带的都是等式约束条件,那这属于等式约束优化;如果函数 f ( x ⃗ ) f(\vec{x}) f(x)附带有不等式约束条件,那这属于不等式约束优化。面对不同的优化问题,需要不同的方法来解决。
无约束优化
用数学的语言表达出来,就是
min x ⃗ f ( x ⃗ ) , \displaystyle \min_{\vec{x}} f(\vec{x}), xminf(x),
因为求最大值和最小值可以相互转化,所以都以求最小值为例。对于一元函数 f ( x ) f(x) f(x)来说,大家都知道通过 f ′ ( x ) = 0 f^\prime(x)=0 f′(x)=0来找到 x ∗ x^* x∗使 f ( x ∗ ) f(x^*) f(x∗)达到最小值。对于 d d d元函数 f ( x ⃗ ) f(\vec{x}) f(x)来说,方法类似,通过方程组
∂ f ∂ x 1 = 0 , ∂ f ∂ x 2 = 0 , … , ∂ f ∂ x d = 0 , ① \frac{\partial f}{\partial x_1}=0,\frac{\partial f}{\partial x_2}=0,…,\frac{\partial f}{\partial x_d}=0,① ∂x1∂f=0,∂x2∂f=0,…,∂xd∂f=0,①
找到 x ⃗ ∗ = ( x 1 ∗ , x 2 ∗ , … , x d ∗ ) \vec{x}^*=(x_1^*,x_2^*,…,x_d^*) x∗=(x1∗,x2∗,…,xd∗)使 f ( x ⃗ ∗ ) f(\vec{x}^*) f(x∗)达到最小值。最小二乘法就采用了这样的思想。这类方法找到的是精确的解析解。但是,式①的方程组有可能很复杂,甚至有可能不存在解析解。那么,求解数值解(近似解)的各种方法应运而生。今天就为大家介绍其中的梯度下降法(Gradient Descent)。
- 梯度下降法
以二元函数 f ( x , y ) f(x,y) f(x,y)为例,假定最小值为 f ( x ∗ , y ∗ ) f(x^*,y^*) f(x∗,y∗),我们的目标就是找到 ( x ∗ , y ∗ ) (x^*,y^*) (x∗,y∗)。梯度下降法认为,若不能解出 ( x ∗ , y ∗ ) (x^*,y^*) (x∗,y∗),那我就构造序列 ( x 0 , y 0 ) , ( x 1 , y 1 ) , … (x_0,y_0),(x_1,y_1),… (x0,y0),(x1,y1),…满足:
f ( x i + 1 , y i + 1 ) < f ( x i , y i ) , i = 0 , 1 , 2 , … , f(x_{i+1},y_{i+1})<f(x_{i},y_{i}),i=0,1,2,…, f(xi+1,yi+1)<f(xi,yi),i=0,1,2,…,
不断逼近 f ( x ∗ , y ∗ ) f(x^*,y^*) f(x∗,y∗),最后总能得到 ( x ∗ , y ∗ ) (x^*,y^*) (x∗,y∗)的近似解。那么,如何构造序列 ( x 0 , y 0 ) , ( x 1 , y 1 ) , … (x_0,y_0),(x_1,y_1),… (x0,y0),(x1,y1),…呢?我们从几何的角度入手。
函数图像 z = f ( x , y ) z=f(x,y) z=f(x,y)是3维的,要寻找的序列是2维平面里的多个点,于是我们将函数图像简化为2维平面上的等高线,如:
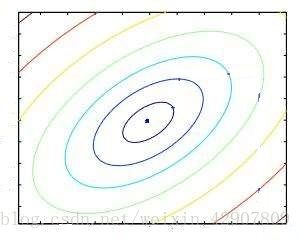
每一条等高线都是由函数值 z z z相等的相邻各点 ( x , y ) (x,y) (x,y)相连而成,当然实际上应该有无数条等高线,这里只是象征性地画了几条。我们发现,任取一点作为序列起点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0), ( x 0 , y 0 ) (x_0,y_0) (x0,y0)移动一下到函数值 z z z更小的等高线上,就形成了 ( x 1 , y 1 ) (x_1,y_1) (x1,y1); ( x 1 , y 1 ) (x_1,y_1) (x1,y1)移动一下到函数值 z z z更更小的等高线上,就形成了 ( x 2 , y 2 ) (x_2,y_2) (x2,y2); ( x 2 , y 2 ) (x_2,y_2) (x2,y2)移动一下到函数值 z z z更更更小的等高线上,就形成了 ( x 3 , y 3 ) (x_3,y_3) (x3,y3);不断重复该过程,如:
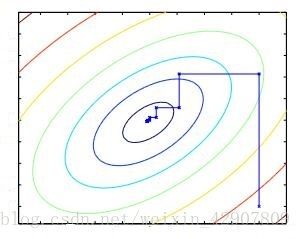
我们就能构建出序列 ( x 0 , y 0 ) , ( x 1 , y 1 ) , … (x_0,y_0),(x_1,y_1),… (x0,y0),(x1,y1),…。大家都知道,一次移动其实就是一个向量,点经过一次移动后的位置其实就是点的坐标加上一个向量。所以找到这些向量,就能确定序列 ( x 0 , y 0 ) , ( x 1 , y 1 ) , … (x_0,y_0),(x_1,y_1),… (x0,y0),(x1,y1),…的值。我们先来分析下这些向量满足的条件:
(1)方向:首先肯定是往函数值 z z z下降的方向;其次考虑到效率,肯定越快越好。所以该方向应该是在当前位置函数值 z z z下降最快的方向。
(2)大小:首先肯定不能过大,因为有可能会错过最小函数值的等高线;其次肯定不能过小,因为需要移动更多次。所以该大小应该适中。
满足条件的向量们,你们在哪?这时,“梯度”跑了出来。
梯度
对于函数 f ( w 1 , w 2 , … , w n ) f(w_1,w_2,…,w_n) f(w1,w2,…,wn),它的偏导数向量:
( ∂ f ∂ w 1 , ∂ f ∂ w 2 , … , ∂ f ∂ w n ) , (\frac{\partial f}{\partial w_1},\frac{\partial f}{\partial w_2},…,\frac{\partial f}{\partial w_n}), (∂w1∂f,∂w2∂f,…,∂wn∂f),
被称为函数 f ( w 1 , w 2 , … , w n ) f(w_1,w_2,…,w_n) f(w1,w2,…,wn)的梯度,记作 g r a d f ( w 1 , w 2 , … , w n ) grad\ f(w_1,w_2,…,w_n) grad f(w1,w2,…,wn) 或 ∇ f ( w 1 , w 2 , … , w n ) \nabla f(w_1,w_2,…,w_n) ∇f(w1,w2,…,wn)。在给定点 ( w 1 ∗ , w 2 ∗ , … , w n ∗ ) (w_1^*,w_2^*,…,w_n^*) (w1∗,w2∗,…,wn∗)处的梯度 ∇ f ( w 1 ∗ , w 2 ∗ , … , w n ∗ ) \nabla f(w_1^*,w_2^*,…,w_n^*) ∇f(w1∗,w2∗,…,wn∗)就为:
( ∂ f ∂ w 1 ∗ , ∂ f ∂ w 2 ∗ , … , ∂ f ∂ w n ∗ ) . (\frac{\partial f}{\partial w_1^*},\frac{\partial f}{\partial w_2^*},…,\frac{\partial f}{\partial w_n^*}). (∂w1∗∂f,∂w2∗∂f,…,∂wn∗∂f).
那么 ∇ f ( w 1 ∗ , w 2 ∗ , … , w n ∗ ) \nabla f(w_1^*,w_2^*,…,w_n^*) ∇f(w1∗,w2∗,…,wn∗)表示什么意思呢?它是一个向量,它的方向就表示函数值在点 ( w 1 ∗ , w 2 ∗ , … , w n ∗ ) (w_1^*,w_2^*,…,w_n^*) (w1∗,w2∗,…,wn∗)处上升最快的方向,它的大小就表示函数值沿该方向的上升率。于是, − ∇ f ( w 1 ∗ , w 2 ∗ , … , w n ∗ ) -\nabla f(w_1^*,w_2^*,…,w_n^*) −∇f(w1∗,w2∗,…,wn∗)的方向就表示函数值在点 ( w 1 ∗ , w 2 ∗ , … , w n ∗ ) (w_1^*,w_2^*,…,w_n^*) (w1∗,w2∗,…,wn∗)处下降最快的方向,大小就表示函数值沿该方向的下降率。
看来, − ∇ f ( x 0 , y 0 ) , − ∇ f ( x 1 , y 1 ) , − ∇ f ( x 2 , y 2 ) , … -\nabla f(x_0,y_0),-\nabla f(x_1,y_1),-\nabla f(x_2,y_2),… −∇f(x0,y0),−∇f(x1,y1),−∇f(x2,y2),…就是我们要找的向量们了。但是这些向量的大小是已经确定的,我们不知道到底适不适中,于是我们给每个向量乘以一个学习率 α i , i = 0 , 1 , 2 , … \alpha_i,i=0,1,2,… αi,i=0,1,2,…。 α i \alpha_i αi可以一样,也可以不一样。这里我们就简单采用 α 0 = α 1 = … = α \alpha_0=\alpha_1=…=\alpha α0=α1=…=α。最终,有
( x 0 , y 0 ) = 随 机 值 (x_0,y_0)=随机值 (x0,y0)=随机值
( x 1 , y 1 ) = ( x 0 , y 0 ) − α ∇ f ( x 0 , y 0 ) , (x_1,y_1)=(x_0,y_0)-\alpha \nabla f(x_0,y_0), (x1,y1)=(x0,y0)−α∇f(x0,y0),
( x 2 , y 2 ) = ( x 1 , y 1 ) − α ∇ f ( x 1 , y 1 ) , (x_2,y_2)=(x_1,y_1)-\alpha \nabla f(x_1,y_1), (x2,y2)=(x1,y1)−α∇f(x1,y1),
( x 3 , y 3 ) = ( x 2 , y 2 ) − α ∇ f ( x 2 , y 2 ) , (x_3,y_3)=(x_2,y_2)-\alpha\nabla f(x_2,y_2), (x3,y3)=(x2,y2)−α∇f(x2,y2),
… … …
直到函数值的变化非常小的时候停止。
推广到 d d d元函数 f ( x ⃗ ) f(\vec{x}) f(x)是一样的方法,这里就不赘述了。
当然,大家会发现一个问题,我们在函数值变化非常小时就停止迭代,有可能只找到了局部最小值,而不是全局最小值。
ps:图片来自网络,侵权立删。