论文《CROSS: Cross-Platform Recommendation for Social E-Commerce》阅读
论文《CROSS: Cross-Platform Recommendation for Social E-Commerce》阅读
- 论文概况
- 论文亮点
- Introduction
- Related Work
- Data & Preliminary Study
- Data
- Preliminary Study
- Q1. 社交媒体的购物占比
- Q2. 不同平台购物模式区别
- Q3. 好友关系的影响
- Preliminaries
- 问题形式化
- baselines
- CMF(Collective Matrix Factorization)
- SocialMF
- Our Solutions
- APP平台部分
- 社交媒体部分
- 训练
- 损失函数
- 训练过程
- 分类模型场景
- 总结
论文概况
论文《CROSS: Cross-Platform Recommendation for Social E-Commerce》提出了一个跨平台的社交电子商务推荐算法CROSS,发表在了SIGIR 2019上,SIGIR是信息检索的顶会,CCF A。
论文地址:paper
数据集地址:dataset
代码地址:未公布
论文亮点
本文主要解决了在社交购物平台上的推荐问题,主要结合了跨平台推荐(cross-platform recommendation)和社交推荐(social recommendation)两部分来解决问题:跨平台部分作者将传统平台和社交购物分开作为两个平台进行结合;社交推荐部分作者同样将用户的表示分为两部分,静态部分不受其他用户影响,来自传统平台,而动态部分则来自社交购物平台,由社交关系影响形成。具体影响关系后文将会展开。
Introduction
作者强调了社交网络购物平台的重要性,并强调使用基于传统平台(APP)设计的推荐系统并不适用于社交网络购物平台。举例来说,我们在淘宝或者京东上买东西,这就是基于传统平台,使用专门的购物APP进行购物的,商家会根据推荐算法为我们推荐他们认为我们喜欢的商品。同时,社交网络越来越发达,我们可以一键共享至微信,在微信小程序端打开购物链接。作者认为,我们在微信小程序端的购物行为和在APP端的购物行为是有不同的,因此应该专门为微信小程序端设计一套专门的推荐系统。这就是这篇论文的背景。
作者从两方面对提出的问题进行解决:
- 跨平台用户行为建模:作者认为不同平台用户的行为是不同的,应该对不同平台用户的表示进行专门的设计
- 社交媒体中用户行为的复杂性:作者认为以往的研究中,为了表示用户的行为受到其好友的影响,而去减小用户和好友之间的L2距离是不合适的。作者认为尽管受到好友的影响,但是同时用户应该有一部分固定的行为习惯是不受影响的。因此作者认为用户表示应该包含两部分:固定部分以及受好友影响部分。
接下来,我将按照文章顺序进行介绍。不会一字一句地进行翻译,而是介绍作者的中心意思。
Related Work
介绍之前,我们先简要介绍矩阵分解算法的核心思想:给定一个平台用户(user)和物品(item)之间的关系矩阵 R R R(可以是购买,浏览或者其他,只要表明用户与物品之间的关系即可),推荐系统(RS,Recommender System)要解决的问题就是根据关系矩阵(稀疏矩阵) R R R中已有的值去预测空白值。而矩阵分解算法就是根据矩阵 R ∈ R m × n R\in\mathbb{R}^{m\times n} R∈Rm×n,构造用户矩阵 U ∈ R m × k U\in \mathbb{R}^{m\times k} U∈Rm×k,以及物品矩阵 V ∈ R k × n V\in \mathbb{R}^{k\times n} V∈Rk×n,使得 R = U V R=UV R=UV,其中 m m m、 n n n、 k k k分别表示用户数量,物品数量以及潜在空间(latent space)的维度。 U U U的任意一行 u i T ∈ R k u_i^{\mathsf{T}}\in\mathbb{R}^{k} uiT∈Rk表示用户 i i i, V V V的任意一列 v j ∈ R k v_j\in\mathbb{R}^{k} vj∈Rk表示物品 j j j, u i T v j u_i^{\mathsf{T}}v_j uiTvj及表示用户 i i i与物品 j j j之间的关系。
矩阵分解算法通过下式完成推荐:
min U , V R − U V (1) \min_{U,V}{R-UV} \tag{1} U,VminR−UV(1)
有了上面的基础知识,作者在这一部分主要介绍了跨平台推荐和社会推荐两部分内容。
- 跨平台推荐(Cross-platform Recommendation):用户在不同平台中有不同的购物行为,但是用户本身的表示(嵌入,Embedding)应该是相同的。因此只需要将用户(user)的表示以及不同平台中物品(item)的表示分别进行矩阵分解(Matrix Factorization)算法的拟合即可。代表算法为CMF(Collective Matrix Factorization)
- 社交推荐(Social Recommendation):传统的矩阵分解算法如上式(1)所示,在此基础上,加入社交正则化项。社交正则化项是通过缩小用户与其好友之间的距离达到的,通过这一手段可以在保证矩阵分解的同时使得用户的表示与好友相关。作者认为这些方法的不可取之处在于用户的embedding与其好友都是相互影响的,作者认为每个用户应该都有一个固定的行为习惯不受好友关系影响。
Data & Preliminary Study
Data
作者的数据集是自己构造的,使用2017/06/01至2017/06/30这一个月的数据,包含APP和微信购物两个通道的购买、加购物车、浏览数据以及用户之间的好友关系。这一部分比较出彩的是对数据集的分析部分,通过分析,作者自然而然地引出了后续的模型解释。
Preliminary Study
作者这一部分主要对数据进行了全面的分析,试图挖掘对社交购物专门设计推荐系统的必要性。由此引发出一下三个问题:
- Q1. 社交媒体的购物占比如何?
- Q2. APP和社交媒体购物模式一样吗?
- Q3. 好友关系会影响社交平台购物吗?
Q1. 社交媒体的购物占比

由原文的图3可以看到,社交媒体加购物车和购买行为已经与传统APP势均力敌。
Q2. 不同平台购物模式区别
v i e w − b u y − r a t i o = # v i e w # b u y (2) view-buy-ratio = \frac{\#view}{\#buy} \tag{2} view−buy−ratio=#buy#view(2)
式(2)用来表示单一用户的浏览-购物比,比值越大,表示该用户越犹豫,就是总看不买。
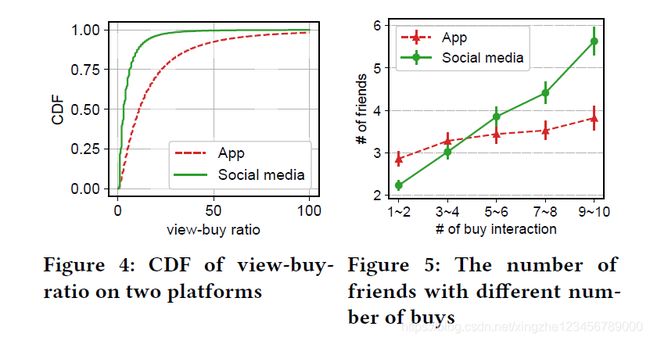
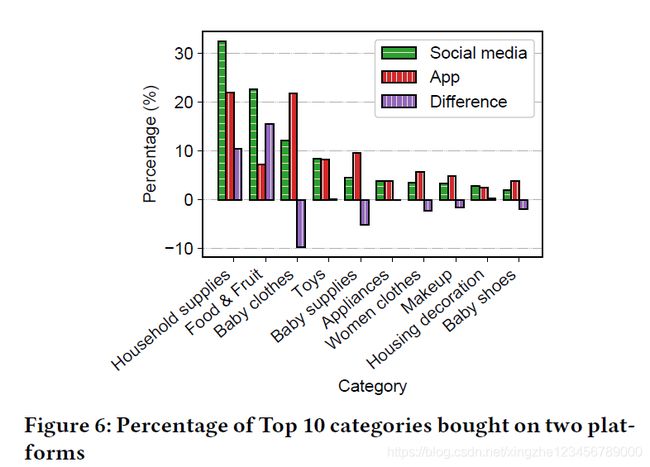
图4应该这样分析,画一条平行于横轴的线,APP上的浏览-购物比总是大于社交媒体上的,证明APP上的购物体验趋向于犹豫,APP上的购物体验趋向于果断。这与直觉相符,因为在APP上购物更加方便,我们也总会多加比较以后才会购买。图6可以看到在APP上和微信小程序端占比较大的物品是不重叠的,大家在微信端倾向于购买不用太多比较的东西。
也因此说明了在微信端使用APP端的推荐系统是不合适的。
Q3. 好友关系的影响
由图5可以看到,微信端好友越多,就会趋向于更多的购物行为;而在APP上,影响不大。因此说明了微信端购物受好友的影响是很大的。这也引出了后续关于用户的静态表示和动态表示。
Preliminaries
问题形式化
R ( A ) ∈ R M × N R^{(A)}\in\mathbb{R}^{M\times N} R(A)∈RM×N表示APP上的user-item interaction 矩阵(A表示Auxiliary), R ( T ) ∈ R M × N R^{(T)}\in\mathbb{R}^{M\times N} R(T)∈RM×N表示微信端的user-item interaction 矩阵(T表示Target), I ( A ) I^{(A)} I(A)和 I ( T ) I^{(T)} I(T)表示对应的指标矩阵(indicator matirces)。(这里指标矩阵应该是包含0和1的二值矩阵,用户 u u u 购买过物品 i i i ,则 I u i = 1 I_{ui}=1 Iui=1,否则为0)。使用矩阵分解法的APP端用户表示和物品表示分别是 P ( A ) ∈ R K × M P^{(A)}\in\mathbb{R}^{K\times M} P(A)∈RK×M, P ( T ) ∈ R K × N P^{(T)}\in\mathbb{R}^{K\times N} P(T)∈RK×N; 微信端用户表示和物品表示分别是 Q ( A ) ∈ R K × M Q^{(A)}\in\mathbb{R}^{K\times M} Q(A)∈RK×M, Q ( T ) ∈ R K × N Q^{(T)}\in\mathbb{R}^{K\times N} Q(T)∈RK×N。同时,微信端用户的好友关系矩阵 S ∈ R M × M S\in\mathbb{R}^{M\times M} S∈RM×M 也是已知的, s u v = 1 s_{uv}=1 suv=1 表示u和v是好友关系,反之, s u v = 0 s_{uv}=0 suv=0 表示不是好友关系。
则问题可以形式化为:
给定 R ( A ) R^{(A)} R(A), R ( T ) R^{(T)} R(T)以及 S S S,求 R ( T ) R^{(T)} R(T)的缺失部分。
baselines
CMF(Collective Matrix Factorization)
CMF对于多个平台的购买行为,使用相同的user embedding和不同的item embedding,因此可以协同使用多个平台的用户信息,从而得到更好的表示结果。具体的,使用下面的目标函数进行优化:
min P ( A ) , P ( T ) , Q ∑ u = 1 M ∑ i = 1 N I i j ( T ) ( R u i ( T ) − p u ( T ) q i ) 2 + I i j ( A ) ( R u i ( A ) − p u ( A ) q i ) 2 (3) \min_{P^{(A)}, P^{(T)},Q}\sum\limits_{u=1}^{M}\sum\limits_{i=1}^{N}{I}_{ij}^{(T)}(R_{ui}^{(T)}-p_u^{(T)}q_i)^2 + I_{ij}^{(A)}(R_{ui}^{(A)}-p_u^{(A)}qi)^2 \tag{3} P(A),P(T),Qminu=1∑Mi=1∑NIij(T)(Rui(T)−pu(T)qi)2+Iij(A)(Rui(A)−pu(A)qi)2(3)
上式以及后文所有式子的正则化项均已省略。
在式(3)中,我们可以看到q(item)的表示是统一的,而user的表示随着平台的变化而变化,这样就可以实现Cross-Platform Recommendation的目标。如图7(a)所示,结合不同平台A和T,使用不同的user表示,与相同的物品表示进行相乘,用以表示用户和物品之间的关系。通过这样的方式,可以整合两个平台之间的item信息。
SocialMF
该方法假定好友之间的购物行为是相似的。因此,应保证user和其好友的embedding之间的距离足够小。因此,可以得到下述的目标函数:
min P ( T ) , Q ∑ u = 1 M ∑ i = 1 N I i j ( R u i − p u ⋅ q i ) 2 + ∑ u = 1 M ( p u − ∑ v ∈ N u S u v p v ) 2 (4) \min_{P^{(T)},Q}\sum\limits_{u=1}^{M}\sum\limits_{i=1}^{N}I_{ij}(R_{ui}-p_u \cdot q_i)^2 + \sum\limits_{u=1}^{M}(p_u-\sum\limits_{v\in{N_u}}{S_{uv}p_v})^2 \tag{4} P(T),Qminu=1∑Mi=1∑NIij(Rui−pu⋅qi)2+u=1∑M(pu−v∈Nu∑Suvpv)2(4)
其中, N u N_u Nu表示用户 u u u 的好友集合。正如图7(b)所示的那样,矩阵 R R R由用户矩阵P和物品矩阵Q相乘进行拟合,同时矩阵P的每一行(每个用户)又与其好友保持最小的L2距离,因此在矩阵分解的同时使用了用户的好友关系信息。但是作者指出,这个模型的缺点在于用户的所有属性都收到其好友的影响,而这与现实是不相符合的。结合实际,我们知道我们不可能所有的购买行为都是因为我们的好友影响而完成的,我们自己也有较为稳定的、维持不变的购物偏好。
Our Solutions
这一部分作者对模型的具体细节进行了讲解。整个模型的原理如图7©所示,原理相当于结合了CMF和SocialMF。
模型的损失函数由两部分构成:
L = L ( A ) + L ( T ) (5) L=L^{(A)}+L^{(T)} \tag{5} L=L(A)+L(T)(5)
其中, L ( A ) L^{(A)} L(A)表示APP中用户的购物行为的损失, L ( T ) L^{(T)} L(T)表示微信端用户购物函数的损失。
APP平台部分
即 L ( A ) L^{(A)} L(A)部分,由于用户在APP上购买,不存在用户之间的相互影响,因此这部分简单实用MF(矩阵分解)方法进行计算,即
R ^ u i ( A ) = p u ( A ) ⋅ q i (6) \hat{R}_{ui}^{(A)} = p_u^{(A)} \cdot q_i \tag{6} R^ui(A)=pu(A)⋅qi(6)
因此对应的APP部分的平方差损失函数如下:
L ( A ) = ∑ u = 1 M ∑ i = 1 N I i j ( A ) ( R u i ( A ) − p u ( A ) ⋅ q i ) 2 (7) L^{(A)} = \sum\limits_{u=1}^{M}\sum\limits_{i=1}^{N}I_{ij}^{(A)}(R_{ui}^{(A)}-p_u^{(A)} \cdot q_i)^2 \tag{7} L(A)=u=1∑Mi=1∑NIij(A)(Rui(A)−pu(A)⋅qi)2(7)
社交媒体部分
这部分用于学习微信端的用户行为,作者将用户行为分为两部分:1)用户本身的行为,这部分行为是用户自己的行为习惯,不受好友的影响,和在APP购物的习惯是相同的,因此直接使用APP上的用户embedding;2)用户受到好友影响的行为,形式上表现为用户好友embedding的期望。因此,得到下列计算:
R ^ u i ( T ) = R ^ u i ( A ) + R ^ u i ∗ = p u ( A ) ⋅ q i + p u ( T ) ⋅ q i (8) \hat{R}_{ui}^{(T)} = \hat{R}_{ui}^{(A)} + \hat{R}_{ui}^{*} = p_u^{(A)} \cdot q_i + p_u^{(T)} \cdot q_i \tag{8} R^ui(T)=R^ui(A)+R^ui∗=pu(A)⋅qi+pu(T)⋅qi(8)
上式(8)中,我们希望用户 u u u的社交媒体部分( p u ( T ) p_u^{(T)} pu(T))与其好友的社交媒体部分保持接近,即
p ^ u ( T ) = ∑ v ∈ N u S u v p v ( T ) ∑ v ∈ N u S u v = ∑ v ∈ N u S u v p v ( T ) ∣ N u ∣ (9) \hat{p}_u^{(T)} = \frac{\sum\nolimits_{v \in N_u}{S_{uv}p_v^{(T)}}} {\sum\nolimits_{v \in N_u}{S_{uv}}}=\frac{\sum\nolimits_{v \in N_u}{S_{uv}p_v^{(T)}}}{|N_u|} \tag{9} p^u(T)=∑v∈NuSuv∑v∈NuSuvpv(T)=∣Nu∣∑v∈NuSuvpv(T)(9)
对矩阵 S S S进行行归一化,使其每一行加和为1,则可省略分母部分,上式(9)可简写为:
p ^ u ( T ) = ∑ v ∈ N u S u v p v ( T ) (10) \hat{p}_u^{(T)} = \sum\limits_{v \in N_u}{S_{uv}p_v^{(T)}} \tag{10} p^u(T)=v∈Nu∑Suvpv(T)(10)
根据式(10)在矩阵分解算法的基础上加入一个社交归一化项,形式上为 p ^ u ( T ) \hat{p}_u^{(T)} p^u(T) 与 p u ( T ) p_u^{(T)} pu(T) 的平方差之和,即:
L ( T ) = ∑ u = 1 M ∑ i = 1 N I i j ( T ) ( R u i ( T ) − p u ( A ) ⋅ q i − p u ( T ) ⋅ q i ) 2 + λ S ∑ u = 1 M ( p u ( T ) − ∑ v ∈ N u S u v p v ( T ) ) 2 (11) L^{(T)} = \sum\limits_{u=1}^{M}\sum\limits_{i=1}^{N}I_{ij}^{(T)}(R_{ui}^{(T)}-p_u^{(A)} \cdot q_i - p_u^{(T)} \cdot q_i)^2 \\+ \lambda_S\sum\limits_{u=1}^{M}(p_u^{(T)} - \sum\limits_{v \in N_u}{S_{uv}p_v^{(T)}})^2 \tag{11} L(T)=u=1∑Mi=1∑NIij(T)(Rui(T)−pu(A)⋅qi−pu(T)⋅qi)2+λSu=1∑M(pu(T)−v∈Nu∑Suvpv(T))2(11)
其中, λ S \lambda_S λS表示正则化项的权重。
训练
损失函数
综合上述两部分,得到整体的损失函数如下:
min P ( A ) , P ( T ) , Q L = ∑ u = 1 M ∑ i = 1 N I i j ( A ) ( R u i ( A ) − p u ( A ) ⋅ q i ) 2 + ∑ u = 1 M ∑ i = 1 N I i j ( T ) ( R u i ( T ) − p u ( A ) ⋅ q i − p u ( T ) ⋅ q i ) 2 + λ S ∑ u = 1 M ( p u ( T ) − ∑ v ∈ N u S u v p v ( T ) ) 2 (12) \min_{P^{(A)}, P^{(T)},Q} L = \sum\limits_{u=1}^{M}\sum\limits_{i=1}^{N}I_{ij}^{(A)}(R_{ui}^{(A)}-p_u^{(A)} \cdot q_i)^2 \\ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\sum\limits_{u=1}^{M}\sum\limits_{i=1}^{N}I_{ij}^{(T)}(R_{ui}^{(T)}-p_u^{(A)} \cdot q_i - p_u^{(T)} \cdot q_i)^2 \\ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \lambda_S\sum\limits_{u=1}^{M}(p_u^{(T)} - \sum\limits_{v \in N_u}{S_{uv}p_v^{(T)}})^2 \tag{12} P(A),P(T),QminL=u=1∑Mi=1∑NIij(A)(Rui(A)−pu(A)⋅qi)2 +u=1∑Mi=1∑NIij(T)(Rui(T)−pu(A)⋅qi−pu(T)⋅qi)2 +λSu=1∑M(pu(T)−v∈Nu∑Suvpv(T))2(12)
训练过程
作者使用随机梯度下降进行训练,但是具体代码没有给出,原因未知。
分类模型场景
式(12)针对的是回归模型,一般对应的推荐系统中的场景是评分,即给定的 R ( A ) R^{(A)} R(A)、 R ( T ) R^{(T)} R(T)是具体的分值。对应于只有0、 1的分类模型(称之为成对的情况,pairwise case),在推荐系统中,将其称为非显示反馈(implicit feedback)场景,优化函数认为有反馈的互动(interaction)优于无反馈的互动。更详细来讲,分类模型经常对应于购买过/没有购买过、浏览过/没有浏览过、加入过购物车/没有加入过购物车这种非0即1的行为,在这种情况下,推荐系统中给定一个排序,即用户更青睐买过的物品、浏览过的物品、加入购物车的物品,而不喜欢没买过的、没浏览过的、没加入过购物车的物品。因此,在分类场景下,扩展优化函数如下所示:
min p ( A ) , p ( T ) , Q L = ∑ ( u , i , j ) ∈ D S ( A ) ln σ ( x ^ u i j ( A ) ) + ∑ ( u , i , j ) ∈ D S ( T ) ln σ ( x ^ u i j ( T ) ) + λ s ∑ u = 1 M ( p u ( T ) − ∑ v ∈ N u S u v p v ( T ) ) 2 (13) \min_{p^{(A)}, p^{(T)},Q} L = \sum\limits_{(u,i,j)\in D_S^{(A)}} {\ln\sigma(\hat{x}_{uij}^{(A)})} + \sum\limits_{(u,i,j)\in D_S^{(T)}} {\ln\sigma(\hat{x}_{uij}^{(T)})} \\ + \lambda_s \sum\limits_{u=1}^{M}{(p_u^{(T)} - \sum\limits_{v\in N_u}{S_{uv}p_v^{(T)}} )^2} \tag{13} p(A),p(T),QminL=(u,i,j)∈DS(A)∑lnσ(x^uij(A))+(u,i,j)∈DS(T)∑lnσ(x^uij(T))+λsu=1∑M(pu(T)−v∈Nu∑Suvpv(T))2(13)
在上式(13)中,
x ^ u i j ( A ) = R ^ u i ( A ) − R ^ u j ( A ) = p u ( A ) ⋅ q i − p u ( A ) ⋅ q j x ^ u i j ( T ) = R ^ u i ( T ) − R ^ u j ( T ) = ( p u ( A ) ⋅ q i + p u ( T ) ⋅ q i ) − ( p u ( A ) ⋅ q j + p u ( T ) ⋅ q j ) (14) \hat{x}_{uij}^{(A)}=\hat{R}_{ui}^{(A)}-\hat{R}_{uj}^{(A)}=p_u^{(A)} \cdot q_i-p_u^{(A)} \cdot q_j \\ \ \\ \ \\ \hat{x}_{uij}^{(T)} = \hat{R}_{ui}^{(T)}-\hat{R}_{uj}^{(T)} \\ \ \\ = (p_u^{(A)} \cdot q_i + p_u^{(T)} \cdot q_i) - (p_u^{(A)} \cdot q_j + p_u^{(T)} \cdot q_j) \tag{14} x^uij(A)=R^ui(A)−R^uj(A)=pu(A)⋅qi−pu(A)⋅qj x^uij(T)=R^ui(T)−R^uj(T) =(pu(A)⋅qi+pu(T)⋅qi)−(pu(A)⋅qj+pu(T)⋅qj)(14)
其中, σ \sigma σ是sigmoid函数, ( u , i , j ) ∈ D S (u,i,j) \in D_S (u,i,j)∈DS就是根据用户 u u u对于物品 i i i的偏好程度大于物品 j j j的偏好次序形成的三元组集合。
总结
对于论文的实验部分和总结部分这里予以省略。这篇文章将social recommendation和cross-platform进行了很好的结合。