39 组合总和
**
找数组中 加减乘除等于某target 用递归回溯
**
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
个人总结
此类问题,一定会有一个 target 作为递归结束.
一定会有一个 tmp 用来存放递归回溯中的不同值,可以是nums 或者strs
一定会有一个 index 用来标识,对原输入,遍历到哪里了
每次将“输入”第index的值压入tmp,进行下一轮判断。 然后pop
收敛条件,target 命中,或者 index 到头。
class Solution:
def combinationSum(self, nums: List[int], target: int) -> List[List[int]]:
if len(nums) == 0:
return []
# 剪枝是为了提速,在本题非必需
nums.sort()
# 在遍历的过程中记录路径,它是一个栈
path = []
res = []
# 注意要传入 size ,在 range 中, size 取不到
self.dfs(nums, 0, path, res, target)
return res
def dfs(self, nums, begin, path, res, target):
# 先写递归终止的情况
if target == 0:
# Python 中可变对象是引用传递,因此需要将当前 path 里的值拷贝出来
res.append(path[:])
return
for i in range(begin, len(nums)):
residue = target - nums[i]
# “剪枝”操作,不必递归到下一层,并且后面的分支也不必执行
if residue < 0:
break
path.append(nums[i])
# 因为下一层不能比上一层还小,起始索引还从 index 开始
self.dfs(nums, i, path, res, residue)
path.pop()
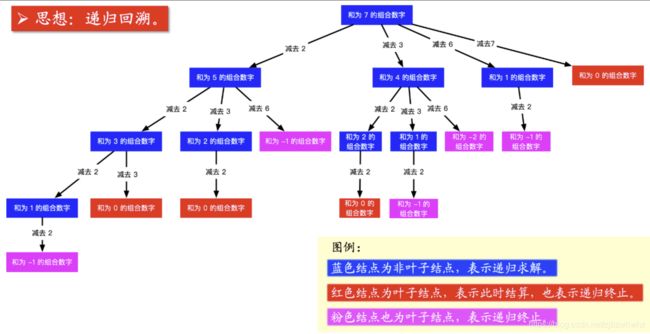
思路:根据示例 1:输入: candidates = [2,3,6,7],target = 7。
- 候选数组里有 2 ,如果找到了 7 - 2 = 5 的所有组合,再在之前加上 2 ,就是 7 的所有组合;
- 同理考虑 3,如果找到了 7 - 3 = 4 的所有组合,再在之前加上 3 ,就是 7 的所有组合,依次这样找下去;
- 上面的思路就可以画成下面的树形图。
其实这里思路已经介绍完了,大家可以自己尝试在纸上画一下这棵树。然后编码实现,如果遇到问题,再看下面的文字。
- 蓝色结点表示:尝试找到组合之和为该数的所有组合,怎么找呢?逐个减掉候选数组中的元素即可;
- 以 target = 7 为根结点,每一个分支做减法;
- 减到 00 或者负数的时候,到了叶子结点;
- 减到 00 的时候结算,这里 “结算” 的意思是添加到结果集;
- 从根结点到叶子结点(必须为 0)的路径,就是题目要我们找的一个组合。
把文字的部分去掉。
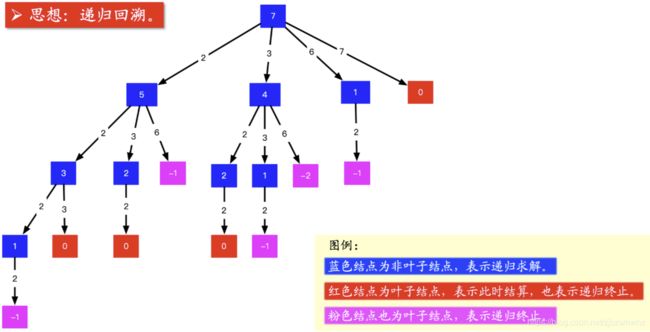
如果这样编码的话,会发现提交不能通过,这是因为递归树画的有问题,下面看一下是什么原因。
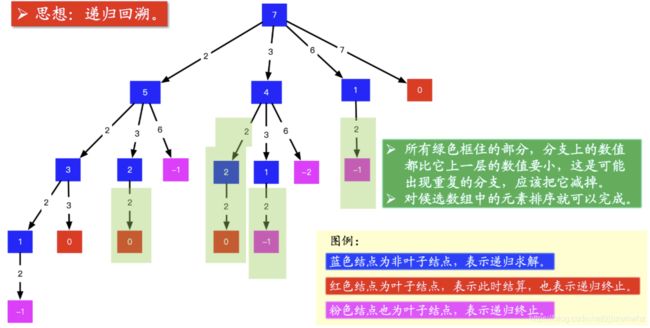
画出图以后,我看了一下,我这张图画出的结果有 44 个 00,对应的路径是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]],而示例中的解集只有 [[7], [2, 2, 3]],很显然,重复的原因是在较深层的结点值考虑了之前考虑过的元素,因此我们需要设置“下一轮搜索的起点”即可(这里可能没有说清楚,已经尽力了)。
去重复
- 在搜索的时候,需要设置搜索起点的下标 begin ,由于一个数可以使用多次,下一层的结点从这个搜索起点开始搜索;
- 在搜索起点 begin 之前的数因为以前的分支搜索过了,所以一定会产生重复。
剪枝提速
- 如果一个数位搜索起点都不能搜索到结果,那么比它还大的数肯定搜索不到结果,基于这个想法,我们可以对输入数组进行排序,以减少搜索的分支;
- 排序是为了提高搜索速度,非必要;
- 搜索问题一般复杂度较高,能剪枝就尽量需要剪枝。把候选数组排个序,遇到一个较大的数,如果以这个数为起点都搜索不到结果,后面的数就更搜索不到结果了。
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> res;
vector<int> mem;
fun(candidates,target,0,mem,res);
return res;
}
void fun(const vector<int> &candidates,int target,int index,vector<int> &mem,vector<vector<int>> &res)
//这里将mem定义为引用可以减少占用内存,提高速度。不定义为内存也正确
{
if(target<0) return;
if(target==0)
{
res.push_back(mem);
return;
}
while(index<candidates.size())
{
mem.push_back(candidates[index]);
fun(candidates,target-candidates[index],index,mem,res);
mem.pop_back();
++index;
}
}
};
python 迭代
class Solution(object):
def combinationSum(self, candidates, target):
"""
:type candidates: List[int]
:type target: int
:rtype: List[List[int]]
"""
candidates = sorted(set(candidates))
result = list()
stack = [(0, list(), target)]
cand_len = len(candidates)
while stack:
i, path, remain = stack.pop()
while i < cand_len:
if path and remain < path[-1]:
break
if candidates[i] == remain:
result.append(path + [candidates[i]])
stack += [(i, path + [candidates[i]], remain - candidates[i])]
i+=1
return result