【精通特征工程】学习笔记（一）

【精通特征工程】学习笔记Day1&1.26&D1-2章&P1-32页

1、机器学习流程&基本概念

• 数据–任务–模型–特征–模型评价
• **数据：**是对现实世界的现象的观测
• **特征：**就是原始数据某个方面的数值表示
• **特征工程：**是指从原始数据中提取特征并将其转换为适合机器学习模型的格式
• 在统计机器学习中，所有数据最终都会转化为数值型特征。因此，所有特征工程最终都会归结为某种数值型特征工程技术

2、简单而又奇妙的数值

2.1 标量、向量、空间

• 单独的数值型特征称为标量，标量的有序列表称为向量，向量位于向量空间中。

2.2 处理计数

2.2.1 二值化

• 将大于等于某个次数的设为1，小于这个次数的设为0

• 二值目标变量是一个既简单又强壮的用户偏好衡量指标

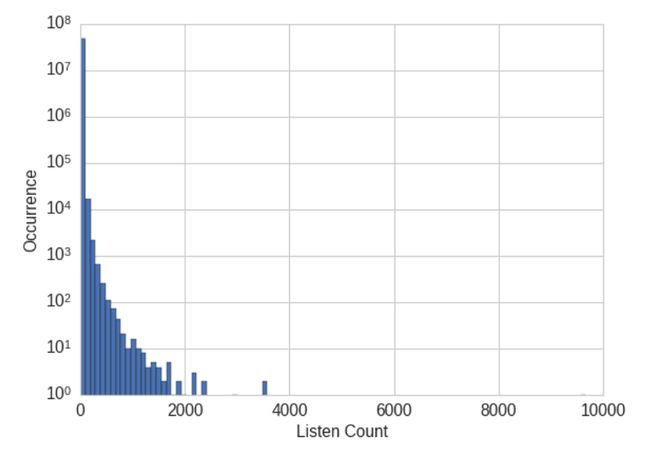
• eg1:歌曲收听次数及人数的原始分布如下，会发现原始的收听次数并不是衡量用户喜好的强壮指标，因此可以进行二值化，如果用户收听了某首歌曲至少一次，那么就认为该用户喜欢该歌曲
  

import pandas as pd
listen_count = pd.read_csv('millionsong/train_triplets.txt.zip',header=None, delimiter='\t')# 表中包含有形式为“用户-歌曲-收听次数”的三元组。只包含非零收听次数。 # 因此，要二值化收听次数，只需将整个收听次数列设为1。
listen_count[2] = 1

2.2.2 区间量化(分箱)

• 区间量化可以将连续型数值映射为离散型数值，可以将这种离散型数值看作一种有序的分箱序列，它表示的是对密度的测量

• 为了对数据进行区间量化，必须确定每个分箱的宽度。有两种确定分箱宽度的方法:固定宽度分箱和自适应分箱

• eg2：商家点评数量数据，点评数量及用户量的分布如下，会发现大多数商家的点评数量很少，但有些商家具有几千条点评，原始的点评数量横跨了若干个数量，一种解决方法是对计数值进行区间量化，然后使用量化后的结果。换言之，将点评数量分到多个箱子里面，去掉实际的计数值
  

（1）固定宽度分箱

• 通过固定宽度分箱，每个分箱中会包含一个具体范围内的数值。这些范围可以人工定制， 也可以通过自动分段来生成，它们可以是线性的，也可以是指数性的

• 例如，可以按 10 年为一段来将人员划分到多个年龄范围中:0~9 岁的在分箱 1 中、10~19 岁的在分箱 2 中

• 要将计数值映射到分箱，只需用计数值除以分箱的宽度，然后取整数部分

• eg3：通过固定宽度分箱对计数值进行区间量化

import numpy as np
small_counts = np.random.randint(0, 100, 20)# 生成20个随机整数，均匀分布在0~99之间
small_counts# 通过除法映射到间隔均匀的分箱中，每个分箱的取值范围都是0~9

np.floor_divide(small_counts, 10)#通过除法映射到间隔均匀的分箱中，每个分箱的取值范围都是0~9

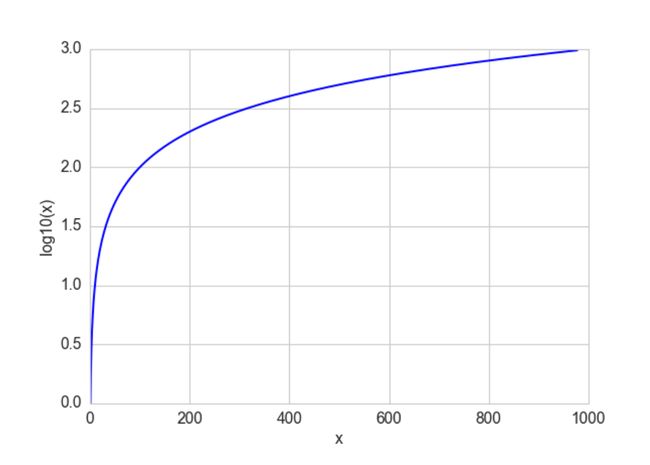
• 当数值横跨多个数量级时，最好按照 10 的幂(或任何常数的幂)来进行分组，如：0-9、 10-99、100-999、1000-9999

• 这时分箱宽度是呈指数增长的，要将计数值映射到分箱，需要取计数值的对数。指数宽度分箱与对数变换的关系非常紧密

• eg4：通过固定宽度分箱对计数值进行区间量化

large_counts = [296, 8286, 64011, 80, 3, 725, 867, 2215, 7689, 11495, 91897,44, 28, 7971, 926, 122, 22222]# 横跨若干数量级的计数值数组

np.floor(np.log10(large_counts))# 通过对数函数映射到指数宽度分箱

（2）分位数分箱

• 如果计数值中有比较大的缺口，就会产生很多没有任何数据的空箱子。根据数据的分布特点，进行自适应的箱体定位，可以使用数据分布的分位数来实现，分位数是可以将数据划分为相等的若干份数的值，如：中位数(即二分位数)、四分位数、十分位数等

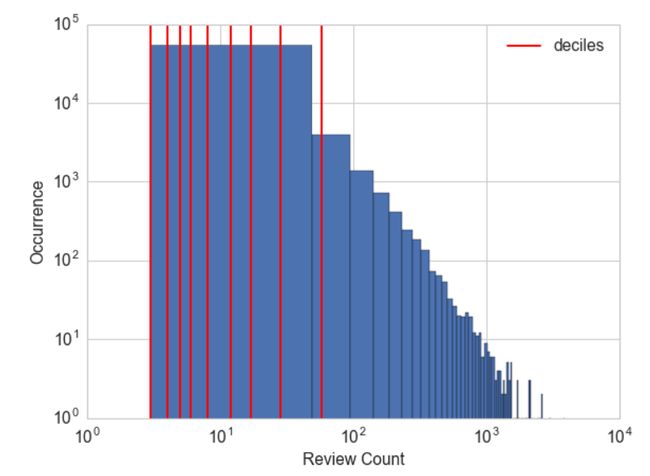
eg5：计算 Yelp 商家点评数量的十分位数

>>> deciles = biz_df['review_count'].quantile([.1, .2, .3, .4, .5, .6, .7, .8, .9])
>>> deciles
0.1 3.0
0.2 4.0
0.3 5.0
0.4 6.0
0.5 8.0
0.6 12.0
0.7 17.0
0.8 28.0
0.9 58.0

在直方图上画出十分位数

• 要计算分位数并将数据映射到分位数分箱中，可以使用 Pandas 库，如例 6所示。

  • pandas.DataFrame.quantile 可以计算分位数
  • pandas.Series.quantile 可以计算分位数
  • pandas.qcut 可以将数据映射为所需的分位数值

• eg6：通过分位数对计数值进行分箱

import pandas as pd # 继续使用例4中的large_couts
pd.qcut(large_counts, 4, labels=False)# 将计数值映射为分位数

# 计算实际的分位数值
large_counts_series = pd.Series(large_counts) 
large_counts_series.quantile([0.25, 0.5, 0.75])

2.3 对数变换

• 对数函数压缩高值区间并扩展低值区间
  

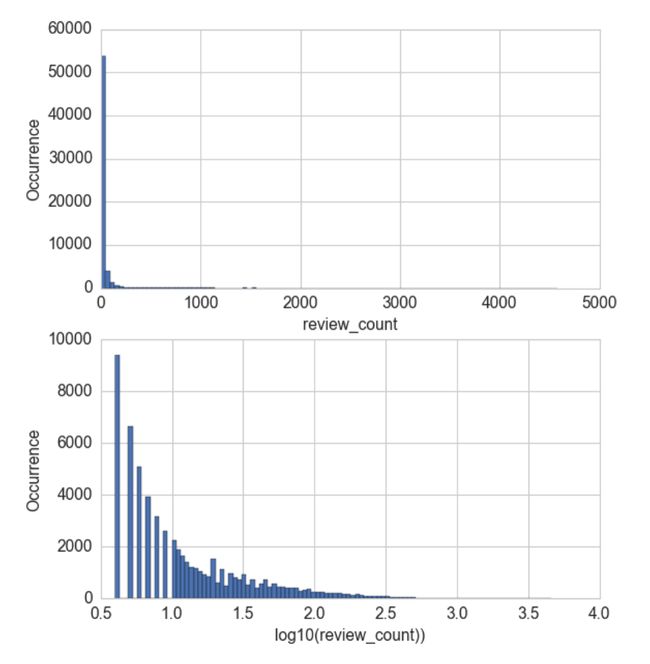
• eg7：对数变换前后的点评数量分布可视化。

  • 分析：比较对数变换前后的 Yelp 商家点评数量的直方图，如下所示，两幅图中的 y 轴都是正常(线性)标度。在下方的图形中，区间 (0.5, 1] 中的箱体间隔很大，是因为在 1 和 10 之间只有 10 个可能的整数计数值。请注意，初始的点评数量严重集中在低计数值区域，但有些异常值跑到了 4000 之外。经过对数变换之后，直方图在低计数值的集中趋势被减弱了，在 x 轴上的分布更均匀了一些

2.3.1 对数变换实战

• 代码demo：使用对数变换后的 Yelp 点评数量预测商家的平均评分

# 使用Yelp点评数据框，计算Yelp点评数量的对数变换值
# 注意，我们为原始点评数量加1，以免当点评数量为0时，对数运算结果得到负无穷大。 
>>> biz_df['log_review_count'] = np.log10(biz_df['review_count'] + 1)

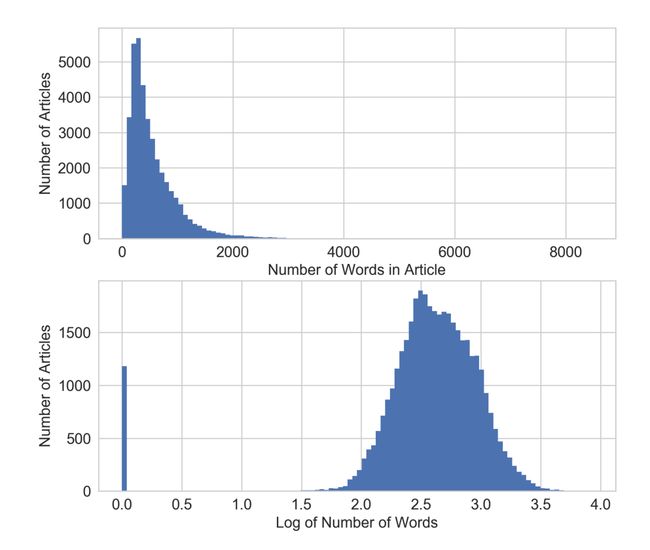
• 代码demo：使用在线新闻流行度数据集中经对数变换后的单词个数预测文章流行度

# 从UCI下载在线新闻流行度数据集，对n_tokens_content特征进行对数变换，这个特征表示的是一篇新闻文章中的单词 # (token)数量。
>>> df['log_n_tokens_content'] = np.log10(df['n_tokens_content'] + 1)

从下图可以看出，对数变换重组了 x 轴，对于那些目标变量值异常巨大(>200000 个分享)的文章，对数变换将它们更多地拉向了 x 轴的右侧，这就为线性模型在输入特征空间的低值端争取了更多的“呼吸空间”。 如果不进行对数变换(下面上方的图)，模型就会面临更大的压力，要在输入变化很小的情况下去拟合变化非常大的目标值。

2.3.2 指数变换:对数变换的推广

• 指数变换是个变换族，对数变换只是它的一个特例。用统计学术语来说，它们都是方差稳定化变换

• 泊松分布是一种 重尾分布，它的方差等于它的均值。因此，它的质心越大，方差就越大，重尾程度也越 大。指数变换可以改变变量的分布，使得方差不再依赖于均值

• 例如，假设一个随机变量X 具有泊松分布，如果通过取它的平方根对它进行变换，那么它的平方根的方差就近似是一 个常数，而不是与均值相等。

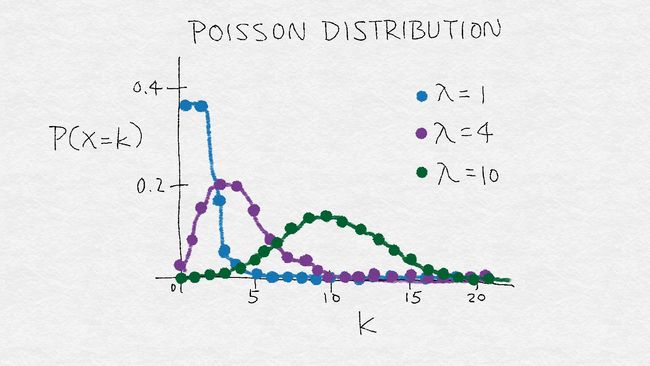
• 下图为泊松分布的粗略表示，这是一个方差随均值变大的分布示例。它表示出了 λ 对泊松分布的影响，λ 表示泊松分布的均值。当 λ 变大时，不仅整个分 布模式向右移动，质量也更加分散，方差随之变大。

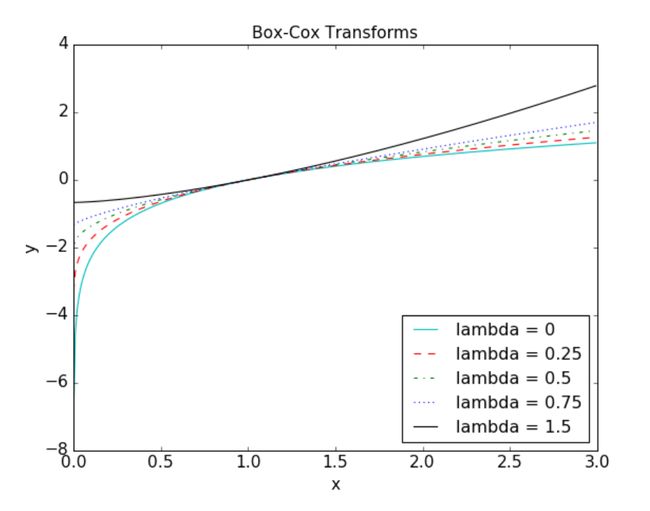
• 平方根变换和对数变换都可以简单推广为 Box-Cox 变换

• 下图展示了 λ = 0(对数变换)、λ = 0.25、λ = 0.5(平方根变换的一种缩放和平移形式)、 λ = 0.75 和 λ = 1.5 时的 Box-Cox 变换。λ 小于 1 时，可以压缩高端值;λ 大于 1 时，起的作 用是相反的。

• 只有当数据为正时，Box-Cox 公式才有效。对于非正数据，我们可以加上一个固定的常数， 对数据进行平移。
  

• 代码demo：对 Yelp 商家点评数量的 Box-Cox 变换

>>> from scipy import stats
# 接上一个例子，假设biz_df包含Yelp商家点评数据。
# Box-Cox变换假定输入数据都是正的。
# 检查数据的最小值以确定满足假定。
>>> biz_df['review_count'].min()
3
# 设置输入参数λ为0，使用对数变换(没有固定长度的位移)。
>>> rc_log = stats.boxcox(biz_df['review_count'], lmbda=0)
# 默认情况下，SciPy在实现Box-Cox转换时，会找出使得输出最接近于正态分布的λ参数。 
>>> rc_bc, bc_params = stats.boxcox(biz_df['review_count'])
>>> bc_params
-0.4106510862321085

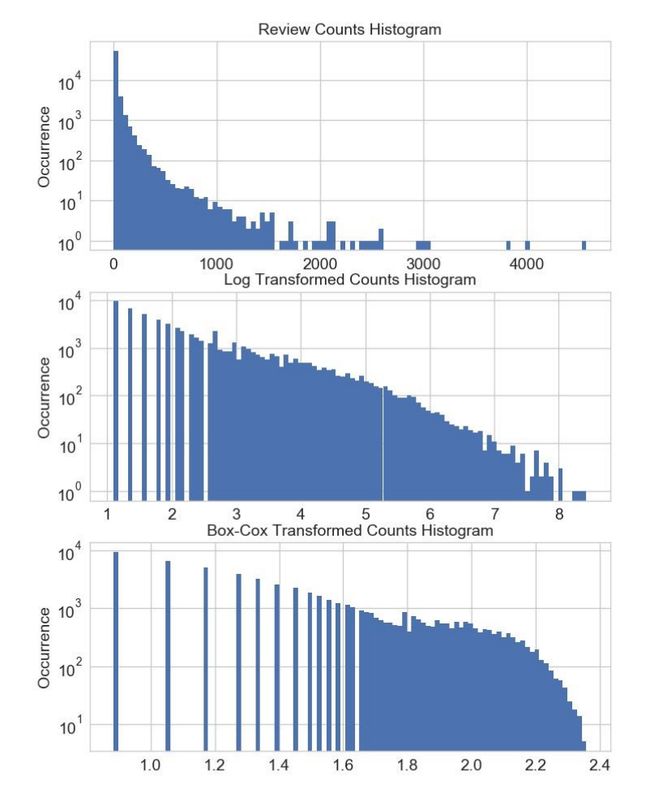
下面为Box-Cox 变换后的 Yelp 商家点评数量直方图(下)，以及初始点评数量直方图(上)和对数变换后的点评数量直方图(中)

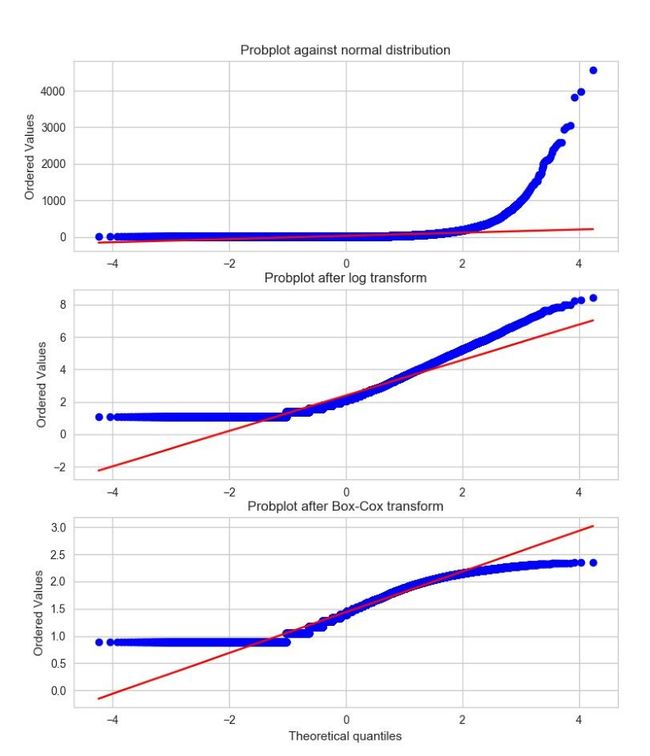
• 概率图是一种非常简单的可视化方法，用以比较数据的实际分布与理论分布， 它本质上是一种表示实测分位数和理论分位数的关系的散点图。
• 下图展示了 Yelp 点评 数据的两种概率图，分别是初始点评数量、变换后点评数量的概率图，并和正态分布进行了对比
• 因为观测数据肯定是正的，而高斯分布可以是负的，所以在负数端，实测分位数和理论分位数不可能匹配。因此，我们只关注正数部分。于是，我们可以看出与正态分布相比，初始的点评数量具有明显的重尾特征。(排序后的值可以达到 4000 以 上，而理论分位数只能到达 4 左右。)普通对数变换和最优 Box-Cox 变换都可以将正尾部 拉近正态分布。
• 根据图形明显可以看出，相比对数变换，最优 Box-Cox 变换对尾部的压缩更强，它使得尾部变平，跑到了红色等值斜线下面。

2.4 特征缩放/归一化

• 有些特征的值是有界限的，比如经度和纬度
• 但有些数值型特征可以无限制地增加，比如计数值
• 有些模型是输入的平滑函数，比如线性回归模型、逻辑回归模型或包含矩阵的模型，它们会受到输入尺度的影响。
• 相反，那些基于树的模型则根本不在乎输入尺度有多 大。
• 如果模型对输入特征的尺度很敏感，就需要进行特征缩放。
• 特征缩放会改变特征的尺度，有些人将其称为特征归一化
• 特征缩放通常对每个特征独立进行

2.4.1 min-max缩放

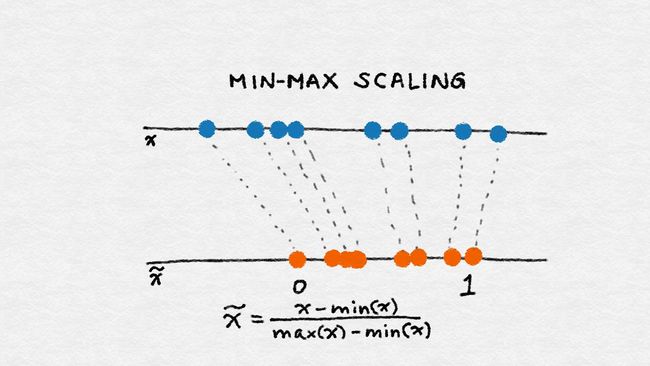
• 令 x 是一个独立的特征值(即某个数据点中的特征值)，min(x) 和 max(x) 分别为这个特征 在整个数据集中的最小值和最大值。min-max 缩放可以将所有特征值压缩(或扩展)到 [0, 1] 区间中
• min-max 缩放的公式如下:
  $$\frac{x-min(x)}{max(x)-min(x)}$$
  

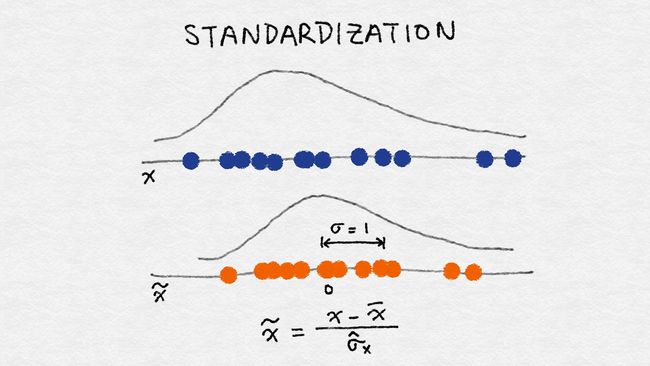
2.4.2 特征标准化/方差缩放

• 特征标准化:它先减去特征的均值(对所有数据点)，再除以方差，因此又称为方差缩放。缩放后的特征均值为 0，方差为 1。如果初始特征服从高斯分布，那么缩放后的特征也服从高斯分布。
• 特征标准化的公式如下：
  $$\hat{x}=\frac{x-mean(x)}{sqrt(var(x))}$$

2.4.3 $l^2$归一化

• 这种归一化技术是将初始特征值除以一个称为 $l^2$范数的量，$l^2$范数又称为欧几里得范数，它的定义如下:
  $$\hat{x}=\frac{x}{||x|{|}_2}$$

• $l^2$范数是坐标空间中向量长度的一种测量。它的定义可以根据著名的毕达哥拉斯定理(给 定一个直角三角形两条直角边的长度，可以求出斜边的长度)导出:
  $$||x|{|}_2=\sqrt{x_1^2+x_2^2+\cdot \cdot \cdot x_m^2}$$

• $l^2$范数先对所有数据点中该特征的值的平方求和，然后算出平方根。经过 $l^2$ 归一化后，特征列的范数就是1

• 不论使用何种缩放方法，特征缩放总是将特征除以一个常数(称为归一化常数)。因此，它不会改变单特征分布的形状

• 代码demo：特征缩放示例

# 加载在线新闻流行度数据集
>>> df = pd.read_csv('OnlineNewsPopularity.csv', delimiter=', ')
# 查看原始数据——文章中的单词数量
>>> df['n_tokens_content'].as_matrix()
array([ 219., 255., 211., ..., 442., 682., 157.])
# min-max缩放
>>> df['minmax'] = preproc.minmax_scale(df[['n_tokens_content']]) >>> df['minmax'].as_matrix()
array([ 0.02584376, 0.03009205, 0.02489969, ..., 0.05215955,0.08048147,  0.01852726])
# 标准化——注意根据标准化的定义，有些结果会是负的
>>> df['standardized'] = preproc.StandardScaler().fit_transform(df[['n_tokens_ content']])
>>> df['standardized'].as_matrix()
array([-0.69521045, -0.61879381, -0.71219192, ..., -0.2218518 ,0.28759248, -0.82681689])
# L2-归一化
>>> df['l2_normalized'] = preproc.normalize(df[['n_tokens_content']], axis=0) 
>>> df['l2_normalized'].as_matrix()
array([ 0.00152439, 0.00177498, 0.00146871, ..., 0.00307663, 0.0047472 ,  0.00109283])

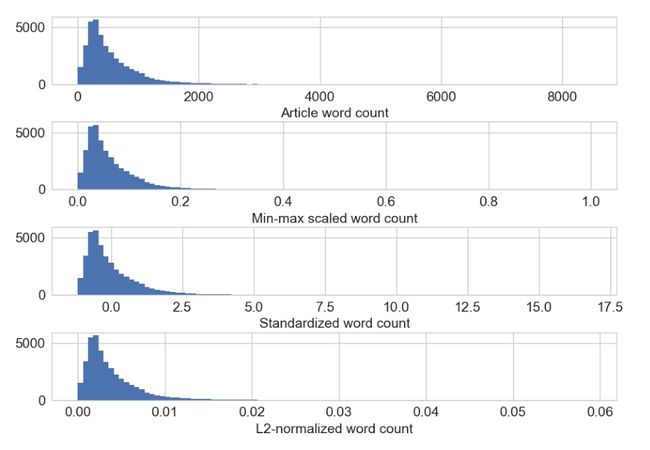
下图为原始及缩放后的新闻文章单词数量。注意只有 x 轴的尺度发生了变化，特征缩放后的分布 形状保持不变

当一组输入特征的尺度相差很大时，就需要进行特征缩放。例如，一个人气很高的商业网 站的日访问量可能是几十万次，而实际购买行为可能只有几千次。如果这两个特征都被模 型所使用，那么模型就需要在确定如何使用它们时先平衡一下尺度。如果输入特征的尺度 差别非常大，就会对模型训练算法带来数值稳定性方面的问题。在这种情况下，就应该对 特征进行标准化。

2.5 交互特征

• 两个特征的乘积可以组成一对简单的交互特征

• 这种相乘关系可以用逻辑操作符 AND 来 类比，它可以表示出由一对条件形成的结果:“该购买行为来自于邮政编码为 98121 的地区”AND“用户年龄在 18 和 35 岁之间”。

• eg： UCI 在线新闻流行度数据集中的交互特征对来预测每篇新闻文章的分享数量

>>> from sklearn import linear_model
>>> from sklearn.model_selection import train_test_split
>>> import sklearn.preprocessing as preproc
# 假设df是一个Pandas数据框，其中包含了UCI在线新闻流行度数据集 >>> df.columns
Index(['url', 'timedelta', 'n_tokens_title', 'n_tokens_content',
            'n_unique_tokens', 'n_non_stop_words', 'n_non_stop_unique_tokens','num_hrefs', 'num_self_hrefs', 'num_imgs', 'num_videos',
            'average_token_length', 'num_keywords', 'data_channel_is_lifestyle',
            'data_channel_is_entertainment', 'data_channel_is_bus',
            'data_channel_is_socmed', 'data_channel_is_tech',
            'data_channel_is_world', 'kw_min_min', 'kw_max_min', 'kw_avg_min',
            'kw_min_max', 'kw_max_max', 'kw_avg_max', 'kw_min_avg', 'kw_max_avg',
            'kw_avg_avg', 'self_reference_min_shares', 'self_reference_max_shares',
            'self_reference_avg_sharess', 'weekday_is_monday', 'weekday_is_tuesday',
            'weekday_is_wednesday', 'weekday_is_thursday', 'weekday_is_friday',
            'weekday_is_saturday', 'weekday_is_sunday', 'is_weekend', 'LDA_00',
            'LDA_01', 'LDA_02', 'LDA_03', 'LDA_04', 'global_subjectivity',
            'global_sentiment_polarity', 'global_rate_positive_words',
            'global_rate_negative_words', 'rate_positive_words',
            'rate_negative_words', 'avg_positive_polarity', 'min_positive_polarity',
            'max_positive_polarity', 'avg_negative_polarity',
            'min_negative_polarity', 'max_negative_polarity', 'title_subjectivity',
            'title_sentiment_polarity', 'abs_title_subjectivity',
            'abs_title_sentiment_polarity', 'shares'],
           dtype='object')
# 选择与内容有关的特征作为模型的单一特征，忽略那些衍生特征 
>>> features = ['n_tokens_title','n_tokens_content','n_unique_tokens', 'n_non_stop_words', 'n_non_stop_unique_tokens','num_hrefs', 'num_self_hrefs', 'num_imgs', 'num_videos', 'average_token_length','num_keywords','data_channel_is_lifestyle','data_channel_is_entertainment', 'data_channel_is_bus', 'data_channel_is_socmed', 'data_channel_is_tech', 'data_channel_is_world']
>>> X = df[features]
>>> y = df[['shares']]
# 创建交互特征对，跳过固定偏移项
>>> X2 = preproc.PolynomialFeatures(include_bias=False).fit_transform(X) >>> X2.shape
(39644, 170)
# 为两个特征集创建训练集和测试集
>>> X1_train, X1_test, X2_train, X2_test, y_train, y_test = train_test_split(X, X2, y, test_size=0.3, random_state=123)
>>> def evaluate_feature(X_train, X_test, y_train, y_test):
     ...     """Fit a linear regression model on the training set and
     ...     score on the test set"""
     ...     model = linear_model.LinearRegression().fit(X_train, y_train)
     ...     r_score = model.score(X_test, y_test)
     ...     return (model, r_score)
# 在两个特征集上训练模型并比较R方分数
>>> (m1, r1) = evaluate_feature(X1_train, X1_test, y_train, y_test)
>>> (m2, r2) = evaluate_feature(X2_train, X2_test, y_train, y_test) 
>>> print("R-squared score with singleton features: %0.5f" % r1) 
>>> print("R-squared score with pairwise features: %0.10f" % r2) 
R-squared score with singleton features: 0.00924
R-squared score with pairwise features: 0.0113276523

注：

• 交互特征的构造非常简单，使用起来却代价不菲。如果线性模型中包含有交互特征对，那它的训练时间和评分时间就会从 O(n) 增加到 O(n2)，其中 n 是单一特征的数量
• 有若干种方法可以绕过高阶交互特征所带来的计算成本。我们可以在构造出所有交互特征之后再执行特征选择，或者，也可以更加精心地设计出少量复杂特征。

2.6 特征选择

• 特征选择技术可以精简掉无用的特征，以降低最终模型的复杂性，它的最终目的是得到一个简约模型，在不降低预测准确率或对预测准确率影响不大的情况下提高计算速度

• 特征选择不是为了减 少训练时间，而是为了减少模型评分时间

• 特征选择技术可以分为以下三类：
  （1） 过滤
  过滤技术对特征进行预处理，以除去那些不太可能对模型有用处的特征。例如，我们可以计算出每个特征与响应变量之间的相关性或互信息，然后过滤掉那些在某个阈值之下 的特征。过滤技术的成本比下面描述的打包技 术低廉得多，但它们没有考虑我们要使用的模型，因此，它们有可能无法为模型选择出正确的特征。我们最好谨慎地使用预过滤技术，以免在有用特征进入到模型训练阶段之 前不经意地将其删除。

  （2）打包方法
  这些技术的成本非常高昂，但它们可以试验特征的各个子集，这意味着我们不会意外地删除那些本身不提供什么信息但和其他特征组合起来却非常有用的特征。打包方法将模型视为一个能对推荐的特征子集给出合理评分的黑盒子。它们使用另外一种方法迭代地对特征子集进行优化。

  （3）嵌入式方法
  这种方法将特征选择作为模型训练过程的一部分。例如，特征选择是决策树与生俱来的 一种功能，因为它在每个训练阶段都要选择一个特征来对树进行分割。另一个例子是 l1 正则项，它可以添加到任意线性模型的训练目标中。l1 正则项鼓励模型使用更少的特 征，而不是更多的特征，所以又称为模型的稀疏性约束。嵌入式方法将特征选择整合为 模型训练过程的一部分。它们不如打包方法强大，但成本也远不如打包方法那么高。与过滤技术相比，嵌入式方法可以选择出特别适合某种模型的特征。从这个意义上说，嵌 入式方法在计算成本和结果质量之间实现了某种平衡。

参考：《精通特征工程》爱丽丝·郑·阿曼达·卡萨丽