论文阅读笔记 Predicting Future Frames using Retrospective Cycle GAN
文章目录
- 0 摘要
- 1 介绍
- 2 相关工作
- 3 解决方案
- 3.1 目标函数
- 3.1.1 Reconstruction losses
- 3.1.2 Adversarial losses
已代码复现,应用于雷达数据集,效果不好,遂放弃
0 摘要
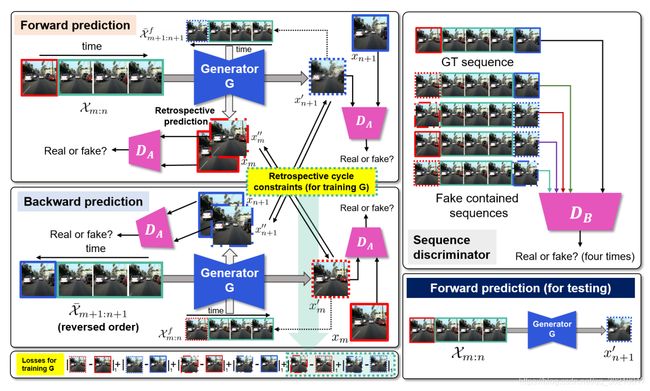
两个Discriminator(一个判断frame是否真实,一个判断frame的sequence是否真实), 一个Generator组成了作者的网络
1 介绍
首先作者的generator可以同时预测未来与过去的帧, 然后作者在预测的帧之间加上了周期一致性。回溯预测(retrospective)的基本思想是,如果预测的未来帧是真实的,即使预测的未来帧被作为输入给出,生成器也应该给出真实的过去帧
2 相关工作
预测图像模糊的原因,实战过的都知道,一部分锅在mse这个评估标准上,有篇论文叫做Deep multi-scale video prediction beyond mean square error提出了一个新的损失函数来解决这个问题。
对于GAN的研究: WGAN和LSGAN修改了discriminator的损失函数来提升训练的稳定性
3 解决方案
frame discriminator判别的是这帧是否是真实的,sequence discriminator判别的是是否这个序列里包含假的帧
使用正向生成一帧,再把它反向预测回去,再生成同样一帧,看前后对比,不能有太大差别 (这是同一个generator和sequence discriminator干的事)
首先要知道输入序列的数学表示:
X m : n = { x m , x m + 1 , … , x n } s . t . m < n \mathcal{X}_{m:n} = \{ x_m, x_{m+1}, \dots, x_n \} \, s.t. \, m < n Xm:n={xm,xm+1,…,xn}s.t.m<n
这是一个序列,包含了 n − m + 1 n-m+1 n−m+1张图片
- 在正向预测过程中, X m : n \mathcal{X}_{m:n} Xm:n作为输入,生成器会输出 x n + 1 ′ x_{n+1}' xn+1′
- 在反向预测过程中, 先把刚才的输入全部反转:
X ‾ m : n = { x n , x n − 1 , … , x m } s . t . m < n \overline \mathcal{X}_{m:n} = \{ x_n, x_{n-1}, \dots, x_m \} \, s.t. \, m < n Xm:n={xn,xn−1,…,xm}s.t.m<n
此时生成器会生成 x m − 1 ′ x_{m-1}' xm−1′ - 将 X m : n \mathcal{X}_{m:n} Xm:n中的 x n x_n xn替换为 x n ′ x_n' xn′, 得到:
X m : n f = { x m : n − 1 ∪ x n ′ } \mathcal{X}_{m:n}^f = \{ x_{m:n-1} \cup x_n' \} Xm:nf={xm:n−1∪xn′}
这里 x n ′ x_n' xn′是通过 X m − 1 : n − 1 \mathcal{X}_{m-1:n-1} Xm−1:n−1来预测得到的,
此时生成器会生成 x n + 1 ′ ′ x_{n+1}'' xn+1′′ - 将 X ‾ m : n \overline \mathcal{X}_{m:n} Xm:n中的 x m x_m xm 替换为 x m ′ x_m' xm′ ,得到:
X ‾ m : n f = { x ‾ m + 1 : n ∪ x m ′ } \overline \mathcal{X}_{m:n}^f = \{ \overline x_{m+1:n} \cup x_m' \} Xm:nf={xm+1:n∪xm′}
这里 x m ′ x_m' xm′是通过 X ‾ m + 1 : n + 1 \overline \mathcal{X}_{m+1:n+1} Xm+1:n+1预测得到的,
此时生成器会生成 x m − 1 ′ ′ x_{m-1}'' xm−1′′
总结下:
1 加了 f ^f f代表序列中最后一帧是fake的
2 加了横线的序列代表反序
3 加了 ′ ' ′ 的代表输入的全是真实帧
4 加了 ′ ′ '' ′′ 的代表输入的最后一帧是fake的(在正向过程中,滚动预测最后全是 ′ ′ '' ′′)
3.1 目标函数
此函数包含了两个重建损失(reconstruction losses)和两个对抗损失(adversarial losses)
L = L i m a g e + λ 1 L L o G + λ 2 L a d v f r a m e + λ 3 L a d v s e q L = L_{image} + \lambda_1 L_{LoG} + \lambda_2 L_{adv}^{frame} + \lambda_3 L_{adv}^{seq} L=Limage+λ1LLoG+λ2Ladvframe+λ3Ladvseq
3.1.1 Reconstruction losses
L i m a g e = ∑ ( p , q ) ∈ S m , n p a i r l 1 ( p , q ) L_{image} = \sum_{(p,q) \in S_{m, n}^{pair}} l_1 (p, q) Limage=(p,q)∈Sm,npair∑l1(p,q)
l1代表的是L1损失函数,即MAE,而 S m , n p a i r S_{m,n}^{pair} Sm,npair代表以下序列(一共牵涉到两个timestep和6组图片):
S m , n p a i r = { ( x m , x m ′ ) , ( x m , x m ′ ′ ) , ( x m ′ , x m ′ ′ ) , ( x n + 1 , x n + 1 ′ ) , ( x n + 1 , x n + 1 ′ ′ ) , ( x n + 1 ′ , x n + 1 ′ ′ ) } \mathcal{S}_{m,n}^{pair} = \{ (x_m, x_m'),(x_m, x_m''),(x_m', x_m''), (x_{n+1}, x_{n+1}'), (x_{n+1}, x_{n+1}''), (x_{n+1}', x_{n+1}'') \} Sm,npair={(xm,xm′),(xm,xm′′),(xm′,xm′′),(xn+1,xn+1′),(xn+1,xn+1′′),(xn+1′,xn+1′′)}
其中 ( x n + 1 , x n + 1 ′ ) (x_{n+1}, x_{n+1}') (xn+1,xn+1′)和 ( x m , x m ′ ) (x_m, x_m') (xm,xm′)是为了最小化正向和反向预测过程中的预测误差
而 ( x n + 1 , x n + 1 ′ ′ ) (x_{n+1}, x_{n+1}'') (xn+1,xn+1′′)和 ( x m , x m ′ ′ ) (x_m, x_m'') (xm,xm′′)是回顾误差(retrospective error), 因为 x n + 1 ′ x_{n+1}' xn+1′是用来预测 x m ′ ′ x_m'' xm′′的,而 x m ′ x_{m}' xm′是用来预测 x n + 1 ′ ′ x_{n+1}'' xn+1′′的
( x m ′ , x m ′ ′ ) (x_m', x_m'') (xm′,xm′′)和 ( x n + 1 ′ , x n + 1 ′ ′ ) (x_{n+1}',x_{n+1}'') (xn+1′,xn+1′′)是周期误差(cyclic),因为分别是正向与反向生成的同一帧拿来作对比
再来看看下一个损失函数:
L L o G = ∑ ( p , q ) ∈ S m , n p a i r l 1 ( L o G ( p ) , L o G ( q ) ) L_{LoG} = \sum_{(p,q) \in S_{m, n}^{pair}} l_1 (LoG(p), LoG(q)) LLoG=(p,q)∈Sm,npair∑l1(LoG(p),LoG(q))
这个损失函数用Laplacian of Gaussian(LoG) 方法计算图片间的损失,来更好地保存图像的边缘(让它不会那么模糊),文章中说是用来去噪(其实本质上还是用Laplacian卷积核来滤波)
3.1.2 Adversarial losses
对抗损失有两个: 帧对抗损失 L a d v f r a m e L_{adv}^{frame} Ladvframe和序列对抗损失 L a d v s e q L_{adv}^{seq} Ladvseq
帧对抗损失主要是为了分类看这一帧是真实的还是虚假的,具体的:
L a d v f r a m e = l A ( X m : n , x n + 1 ) + l A ( X m : n f , x n + 1 ) + l A ( X ‾ m + 1 : n + 1 , x m ) + l A ( X ‾ m + 1 : n + 1 f , x m ) L_{adv}^{frame} = l_A(\mathcal{X}_{m:n}, x_{n+1}) + l_A(\mathcal{X}_{m:n}^f, x_{n+1}) + l_A(\overline \mathcal{X}_{m+1:n+1}, x_{m}) + l_A(\overline \mathcal{X}_{m+1:n+1}^f, x_{m}) Ladvframe=lA(Xm:n,xn+1)+lA(Xm:nf,xn+1)+lA(Xm+1:n+1,xm)+lA(Xm+1:n+1f,xm)
其中 l A ( p , q ) = max G min D A [ ( D A ( q ) − 1 ) 2 + D A ( G ( p ) ) 2 ] l_A (p,q) = \max \limits_G \min \limits_{D_A} [(D_A(q) - 1)^2 + D_A (G(p))^2] lA(p,q)=GmaxDAmin[(DA(q)−1)2+DA(G(p))2]
这里 p p p是 G G G的输入序列, q q q是 G G G的预测帧,这个损失函数是来自least square GAN (论文: Least squares generative
adversarial networks)
序列对抗损失是为了分辨一个输入序列是真实的还是虚假的:
L a d v s e q = l B ( X m : n , x m : n + 1 ) + l B ( X m : n f , x m : n + 1 ) + l B ( X ‾ m + 1 : n + 1 , x m : n + 1 ) + l B ( X ‾ m + 1 : n + 1 f , x m : n + 1 ) L_{adv}^{seq} = l_B(\mathcal{X}_{m:n}, x_{m:n+1}) + l_B(\mathcal{X}_{m:n}^f, x_{m:n+1}) + l_B(\overline \mathcal{X}_{m+1:n+1}, x_{m:n+1}) + l_B(\overline \mathcal{X}_{m+1:n+1}^f, x_{m:n+1}) Ladvseq=lB(Xm:n,xm:n+1)+lB(Xm:nf,xm:n+1)+lB(Xm+1:n+1,xm:n+1)+lB(Xm+1:n+1f,xm:n+1)
其中 l B ( p , r ) = max G min D B [ ( D B ( r ) − 1 ) 2 + ( D B ( G c ( p ) ) ) 2 ] l_B (p, r) = \max \limits_G \min \limits_{D_B} [(D_B(r) - 1)^2 + (D_B(G_c(p)))^2] lB(p,r)=GmaxDBmin[(DB(r)−1)2+(DB(Gc(p)))2] 输入是两个序列: