【文献阅读】 2020-WWW-Attentive Sequential Models of Latent Intent for Next Item Recommendation

说明

1.原文链接。

2.WWW2020其他推荐系统文章。

3.本人及翻译软件的翻译水平有限，粗读即可，精读请看原文。

标题

1.题目：基于潜在意图的注意力序列模型给下一个项目推荐 Attentive Sequential Models of Latent Intent for Next Item Recommendation

2.作者：​​​​​​

摘要

  用户在电子商务服务中表现出不同的意图（如发现商品、购买礼品等），这促使他们以多种方式（如单击、添加到购物车、添加到收藏夹、购买）与各种商品进行交互。为了给出更好的推荐，除了考虑用户的历史交互之外，捕获用户意图也是很重要的。然而，根据定义，这些意图是潜在的，因为我们只观察用户的交互，而不是他们的潜在意图。为了发现这些潜在意图，并有效地利用它们进行推荐，本文提出了一个潜在意图注意序列模型（简称ASLI）。我们的模型首先通过一个自我注意层从用户的交互历史中学习项目相似性，然后使用一个时间卷积网络层从用户对特定类别的行为中获得用户意图的潜在表示。我们使用这个表示来指导注意模型预测下一个项目。我们的实验结果表明，我们的模型能够捕捉用户行为和偏好的动态变化，从而在来自Etsy和Alibaba两个主要电子商务平台的数据集上获得最先进的性能。

1.介绍

  推荐系统的基本目标是从用户可能与之交互的大量项目中推荐候选人。为了实现这一目标，人们提出了各种系统来学习用户的偏好[7，16，23]。工业应用中一种流行的技术是协作过滤（CF），它利用用户最有可能与与其历史交互项目相似的项目交互的观察结果[12]。为了扩展这一概念，各种模型进一步寻求捕捉用户反馈的顺序动态[10，18]。一般来说，这些模型是在单一的交互类型（例如购买或点击）上进行训练的，并且不会进一步将预测分解为不同的动作或意图类型。

  实际上，用户意图可以根据上下文进行更改。考虑一下电子商务中的一个典型设置：用户可以单击项目，将其添加到自己的收藏夹或购物车中，或者在满足条件时购买它们。根据用户的意图和偏好，与其他人相比，她更可能在特定时间点对某个项目执行一种类型的交互。例如，考虑一个用户打算购买产品的情况；很自然，他们将单击、添加到购物车并最终购买的项目之间会有相似之处。因此，要推荐下一次购买，不仅要考虑用户以前购买过什么，还要考虑她过去查看过或添加到购物车中的产品。或者，另一个用户可能只是浏览产品并将其添加到购物车中，而没有立即购买的意图；这类商品可能具有共同的属性（例如价格、美观），但可能与最终购买的商品（例如更便宜的替代品）不同。因此，一个意图（探索）导致不同的互动相比，另一个（购买）。因此，我们可以尝试推荐满足用户当前目的的项目。我们认为这是当前推荐系统无法区分意图类型（甚至交互类型）的潜在限制。

  基于以上观察，我们寻找一个既能发现时间相似性又能捕捉用户意图的系统。这项任务提出了若干挑战。首先，虽然意图和交互是相关的，但它们并不相同；虽然我们可以直接观察用户的交互，但它们的意图是潜在的。因此，必须从用户的交互中推断出潜在意图。此外，用户的意图可能会逐渐演变（交互之间的长期依赖关系）或突然演变（短期依赖关系），这使得很难从嘈杂的操作列表中检测出这种漂移。

  本文针对这些挑战，提出了一种注意序列最新模型（ASLI），它利用自我注意和时间卷积网络来发现项目之间的相似性，捕捉用户的隐藏意图，并关注它们。首先，我们在用户与之交互的所有过去项目上应用自我注意层，以从序列中发现项目的相似性；然后，我们考虑用户在给定类别上执行的交互，并应用时间卷积网络来推断用户的潜在意图。最后，我们应用另一个注意层来解决项目和意图之间的长期和短期依赖关系。这在学习用户对项目的隐藏偏好方面被证明是有效的。我们进一步在两个电子商务网站Etsy和阿里巴巴的真实数据集上展示了我们的模型的有效性。实验表明，该模型能够获得序列预测任务的最新性能。

2.动机

2.1作为交互的类别上的操作

  在电子商务环境中，项目的数量通常远远大于类别的数量，因此用户-项目交互比用户-类别交互要稀疏得多。例如，对于Etsy，稀疏性（观察到的可能交互的分数）在用户项级别仅为0.02%，而在用户类别级别为1.68%。这意味着从行为中推断意图可能比从类别中推断意图更困难。为了更好地理解稀疏性问题，请考虑一个用户在“发现”状态下单击“婚纱”类别中的项目的情况。当她发现有趣的东西时，她把它们放进购物车里。但最终她改变了“购买”的意图，因为她从“礼物和纪念品”类别中找到了更便宜的商品。如图1（a）所示。在用户与“婚纱”中的特定商品进行交互后，可能很难从“礼物和纪念品”中检测出对特定商品的微妙兴趣，因为它们只是各自类别中许多商品中的两个实例。然而，“礼物与纪念品”和“婚纱”之间的联系要简洁得多，而且随着从一个类别到另一个类别的转换数据越来越密集，我们可以更容易地了解用户的兴趣。基于这些原因，我们考虑用户的类别交互以发现潜在意图。

2.2 意图的潜在因素模型

  为了更好地理解意图为什么是一个重要因素，我们尝试在观察到的状态（即项）和我们定义的交互之间建立依赖关系。如果我们希望预测两者，我们将根据过去项目和交互作用的顺序计算它们的联合概率。具体来说，如果我们想计算用户u的下一个项P和下一个交互i的概率，那么联合概率可以表示为：$P(p,i|S_p^u,S_i^u).$ 在这里，$S_p^u$和$S_i^u$ 分别为历史访问的项目和历史进行的交互的序列。有几种方法可以根据变量之间的相互依赖性假设（例如，项依赖于交互，反之亦然）来分解此概率。基于这个假设，分解可以变得简单也可以变得复杂。例如，如果我们假设项依赖于交互作用，那么因子分解变成：$P(i|S_i^u)P(p,i|S_p^u,S_i^u)$。如果假设相互作用依赖于项，则可以导出类似的构造。如果我们假设项目和交互作用都是条件独立的，并且给定了其他潜在变量，那么我们可以简化相同联合概率的分解。我们把这个变量表示为$\theta$。然后，将联合概率分解如下：
$$P(p,i|\theta ,S_p^u,S_i^u)=P(p|\theta ,S_p^u)\times P(i|\theta ,S_i^u)$$
  直观地说，我们在这里引入的潜在变量可以定义为内容的某种表示（购物、浏览、发现新项目等）。我们将此称为用户的“潜在意图”，并设计一个可以参与其中的模型，以便给出更好的推荐。

3. 提出的模型

3.1 问题定义

  表1中描述了标记。我们考虑了从交互项中捕获用户的隐藏意图以获得最相关的下一项推荐的问题。为此，我们将潜在意图定义为用户互动的一种表示形式，可用于预测（或“解释”）下一项和下一项互动。假设$\mathcal{P}=\{1,\dots ,p,\dots ,|\mathcal{P}|\}$是所有产品的集合，$\mathcal{C}=\{1,\dots ,c,\dots ,|\mathcal{C}|\}$是所有类别的集合，并且$\mathcal{A}=\{1,\dots ,a,\dots ,|\mathcal{A}|\}$是所有动作的集合。如果用户对类别$c$中的项目$p$采取动作$a$，则$\mathbf{p}，\mathbf{c}和\mathbf{a}$是产品，类别和动作的对应$d$维嵌入。如上所述，我们已将互动定义为特定类别（即$\mathbf{i}=\mathbf{c}+\mathbf{a}$）中动作的组合。然后，我们将问题表达如下：给定一系列产品和用户交互，${\mathcal{S}}^u=(<{\mathbf{p}}^1,{\mathbf{i}}^1>,<{\mathbf{p}}^2,{\mathbf{i}}^2>,\dots ,<{\mathbf{p}}^{|{\mathcal{S}}^u|},{\mathbf{i}}^{|{\mathcal{S}}^u|}>)$，在每个步骤中，目标是捕获隐藏的或潜在的意图，并使用它来预测下一项和互动，即给定$(<{\mathbf{p}}^1,{\mathbf{i}}^1>,\dots ,<{\mathbf{p}}^{|{\mathcal{S}}^u|-1},{\mathbf{i}}^{|{\mathcal{S}}^u|-1}>)$，预测$(<{\mathbf{p}}^2,{\mathbf{i}}^2>,\dots ,<{\mathbf{p}}^{|{\mathcal{S}}^u|},{\mathbf{i}}^{|{\mathcal{S}}^u|}>)$，在这里$|{\mathcal{S}}^u|$是用户$u$的序列的长度。

3.2 前言

  3.2.1 自注意力网络。自我注意模型是最近提出的顺序模型，在各种NLP任务中都达到了最先进的性能[21]。自我注意首先尝试计算查询和键之间的相似度得分，并将其用作值的注意权重。在这里，查询，键和值可以是相同的对象（例如，项目序列）。具体来说，自我注意被定义为:
$$Attention(\mathbf{Q},\mathbf{K},\mathbf{V})=softmax(\frac{\mathbf{Q}{\mathbf{K}}^T}{\sqrt{d}})\mathbf{V}........................(1)$$
  其中$\mathbf{Q}$，$\mathbf{K}$和$\mathbf{V}$分别是查询，键和值。这些是通过输入嵌入的线性投影来计算的。特别地,$\mathbf{Q}={\mathbf{S}\mathbf{W}}^Q,\mathbf{K}={\mathbf{S}\mathbf{W}}^K,\mathbf{V}={\mathbf{S}\mathbf{W}}^V$.其中，$\mathbf{S}\in {\mathbb{R}}^{n\times d}$为一个矩阵，它描述具有$d$维输入嵌入的长度为$n$的序列，即$\mathbf{S}=[{\mathbf{e}}^1;\dots ,{\mathbf{e}}^n]。{\mathbf{W}}^Q，{\mathbf{W}}^K，{\mathbf{W}}^V\in {\mathbb{R}}^{d\times d}$为投影矩阵。$\mathbf{Q}$和$\mathbf{V}$之间的注意力得分除以可以避免点积的较大值（尤其是具有很多维数）。为了保持因果关系并防止信息从头到尾泄漏，注意力通过禁止${\mathbf{Q}}_i$和${\mathbf{K}}_j(j>i)$之间的所有链接被修改。注意，由于自注意力操作不知道顺序，所以每个位置被分配一个学习嵌入，该学习嵌入被添加到输入嵌入。这个层的的复杂度由公式1可知为$\mathcal{O}(n^{2}d)$.
  时间卷积网络(TCN).与自注意力相比，卷积具有固定的上下文窗口。我们可以用许多不同的方法进行卷积。在我们的任务中，我们考虑基于固定的核大小在一维空间(即序列)中执行卷积，该核大小在输入序列上滑动并通过一组权重来确定上下文元素的重要性。
  如果我们执行具有权重$\mathbf{W}\in {\mathbb{R}}^{d\times l}$的深度卷积，参数的数量可以从$d^{2}l$减少到$dl$，其中$l$是核宽度。具体地说，输入序列$\mathbf{S}$中每个元素i的输出计算如下：
$$\mathrm{D}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{h}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}(\mathbf{S},{\mathbf{W}}_{\mathrm{c},:},i,c)=\sum _{j=1}^l{\mathbf{W}}_{c,j}\ast {\mathbf{S}}_{i+j-[l+1]/2),c}........................(2)$$
  这里的$c$是当前信道。潜在空间的每一维都可以看作一个信道，所以通常是$c=d$，这一层的计算复杂度为$\mathcal{O}(ndl)$。
  前馈网络(FFN)。虽然自注意力模型和卷积模型都能够通过自适应权重聚集序列信息，但它们仍然是线性模型。为了引入非线性，下一步是将这些模型的输出馈送到两层前馈网络(FFN)。具体地说，如果${\mathbf{o}}^t$是第t步的输出(来自Self-Content或TCN)，则：
$$\mathrm{F}\mathrm{F}\mathrm{N}({\mathbf{o}}^t)={\mathbf{W}}_2(\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}({\mathbf{W}}_1{\mathbf{o}}^t+{\mathbf{b}}_1))+{\mathbf{b}}_2$$
  其中，$\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}$是校正的线性单元激活函数[3]、${\mathbf{W}}_1$和${\mathbf{W}}_2$是$d\times d$的权重矩阵，${\mathbf{b}}_1\&{\mathbf{b}}_2$是$d$维的偏置向量。我们应该注意到，FFN是逐点应用的，即每个步骤的输出分别作为输入。因此，两个步骤的输出之间没有交互，并且防止了任何信息泄漏。由于我们采用的是逐点FFN，其计算复杂度为$\mathcal{O}(n{d}^2)$。

ASLI高级概述

  我们在图1(A)中显示了ASLI的高级摘要。在ASLI中，我们首先将自我注意应用于项目序列，以计算来自所有位置的项目的相似度。我们不再将自我关注应用于这些输出，因为我们想要探索项目序列的哪一部分与用户隐藏的意图最相关。为了捕捉潜在的意图，直观地说，我们需要一个隐藏的表示，而不是用户的行为。如前所述，这带来了独特的挑战，因为用户的逐项操作非常稀疏。为了缓解稀疏性问题，我们的关键建模决策之一是将类别操作视为交互。在ASLI中，我们选择TCN来从这些交互中获取特性，因为它相对较浅且易于并行化。稍后，为了确保这个潜在特征捕捉到意图，我们使用它对下一次交互(通过前馈网络)和下一项(通过共同注意的转换器层)进行双重预测。我们在第一层的输出(计算项目相似性)之间进行共同关注，并发现隐藏的意图，因为我们希望解决它们之间的长期和短期依赖关系，并更好地了解项目与用户意图的相关性。

ASLI

  3.4.1 嵌入层：我们在图1(B)中显示了ASLI的详细架构。我们首先将用户u的训练序列${\mathcal{S}}^u$变换成固定长度(N)的序列，其中$n$表示我们的模型可以处理的最大步数。对于项目$p$、种类$c$和动作$a$，我们有相应的嵌入$\mathbf{p}，\mathbf{c}，\mathbf{c}$，由$\mathbf{c}$和$\mathbf{a}$构造交互嵌入，即$\mathbf{i}$=$\mathbf{c}$+$\mathbf{a}$，如果序列长度大于$n$，则考虑最近的$n$个动作。如果序列长度小于$n$，则向左填充，直到长度为$n$。填充使用恒定的零向量$0$。
  3.4.2 自注意力层：这一层的目标是根据用户的顺序交互发现项目之间的相似性。我们可以通过在项目序列上应用自注意力来计算来自不同位置的项目之间的相似度得分。我们考虑添加到当前项嵌入$\mathbf{p}$[21]的当前步骤或位置$t$的可学习位置嵌入$\mathbf{t}$。这样，我们构建了一个序列矩阵，${\mathbf{S}}_p$使用它来计算查询、键和值，即$\mathbf{Q}={\mathbf{S}}_p{\mathbf{W}}^Q，\mathbf{K}={\mathbf{S}}_p{\mathbf{W}}^K，\mathbf{V}={\mathbf{S}}_p{\mathbf{W}}^V。$最后，我们用等式1并得到输出。然后，我们应用剩余连接来利用任何低级信息[5]和层归一化[1]来稳定和加速训练。图1(b)中的左下角方块显示了它的架构。
  3.4.3 TCN层。在这一层中，我们对相互作用的序列矩阵Si应用深度卷积(公式2)，$\mathrm{D}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{h}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}({\mathbf{S}}_i,\mathbf{W})$，随后是剩余连接和层归一化。这一层(在图1(b)中显示为右下角的块)给了我们潜在的意图表示，我们使用它作为查询来预测下一项。我们还将其用作前馈网络的输入，该网络给出了一个嵌入${\mathbf{o}}_i^t$，以预测下一次交互(图1(b)中的中间块)。
  3.4.5 损失函数。为了训练模型，我们采用了逐点损失，其中我们考虑了一个积极的例子和一个消极的例子[9，13]。因为我们预测每一步中的下一项和下一交互，所以每一步都有一个基本事实，即$p$和$i$。为了预测下一项，我们从数据中随机抽样一个负项(用户以前没有交互过的项)。然后计算模型输出与正反例之间的点积，得到一个分数。此分数用于计算排名损失，按以下方式得到下一项的排名损失：
$${\mathcal{L}}_{ranking}=-\sum _{S^u\in S}\sum _{t\in [1,\dots ,n]}[log(\sigma (r_{o_p^t}))+log(\sigma (r_{o_{p^{{}^{\prime }}}^t}))]$$
  这里，$r_{o_p^t}$是正项$p$的点积，$r_{o_{p^{{}^{\prime }}}^t}$是负项$p^{{}^{\prime }}$的分数。类似地，为了预测下一个交互，我们具有下一个交互$i$的基本事实。然后，我们随机抽样该用户没有观察到的类别-动作对的组合，并构造负交互$i^{{}^{\prime }}$.我们同样计算分数并计算交互损失。具体来说，
$${\mathcal{L}}_{interaction}=-\sum _{S^u\in S}\sum _{t\in [1,\dots ,n]}[log(\sigma (r_{o_i^t}))+log(\sigma (r_{o_{i^{{}^{\prime }}}^t}))]$$
  这里，$r_{o_i^t}$和$r_{o_{i^{{}^{\prime }}}^t}$是正项和负项的交互。我们最终的损失函数为$\mathcal{L}={\mathcal{L}}_{ranking}+{\mathcal{L}}_{interaction}$.

4 实验

  在这一部分中，我们介绍了我们的实验装置和实证结果。我们的实验旨在回答以下研究问题：RQ1：与其他推荐模型相比，我们捕获潜在意图的模型性能如何？RQ2：我们架构的各个组件有什么影响？RQ3：我们模式的培训效率和可扩展性如何？

4.1 数据集

  为了展示ASLI的表现，我们考虑了两个流行的电子商务网站的数据集：阿里巴巴和Etsy。表2显示了预处理后这些数据集的统计数据。按照下一个项目推荐[13，24]的设置，对于每个用户，我们测试最后一个项目，验证之前的项目，并与序列的其余部分一起训练。

  天猫是阿里巴巴提供的公开数据集。最初，它包含来自10,000个用户记录的大约1200万个操作。用户可以执行四种类型的操作，即点击、添加到收藏夹、添加到购物车和购买。对于预处理，我们遵循与[7，8，18]相同的步骤，删除任何交互少于5次的用户或项目。另外，请注意，某些项目可能会被用户多次点击，这可能会导致对某些动作的偏向。为了解决这个问题，我们只考虑用户采取的第一个这样的操作。经过预处理后，我们获得了9883个用户、569,658个项目、6,352个类别和2,454,115个操作。
  Etsy是一个专注于个性化和手工物品的电子商务平台。该数据集包含在2018年10月15日至2018年12月15日期间收集的拥有推荐模块账户的用户的活动日志。在[4]之后筛选数据，这样操作少于20个的所有项目或用户都会被删除。经过处理，它包含6,690个用户、119,310个项目、608个类别和215,227个操作。
  为了公平比较，我们还准备了一个版本的天猫，也就是天猫-Small，它的预处理方式和Etsy一样。它包含6,280个用户、47,759个项目、130个类别和439,497个操作。

4.2 评价指标

  我们报告了推荐系统中两个流行的top-k度量的结果，即：$\mathrm{H}\mathrm{i}\mathrm{t}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e}@\mathrm{k}$和$\mathrm{N}\mathrm{D}\mathrm{C}\mathrm{G}@\mathrm{k}$[7，9]。Hitrate@k是地面真实项在前k个预测项中出现的次数，而NDCG@k(归一化折扣累积增益)是一个位置感知度量，它为较高的位置分配更大的权重。具体地说，如果用户的基本事实项的排名是$ran{k}_u,并且ran{k}_u\le k$，则该用户的$\mathrm{N}\mathrm{D}\mathrm{C}\mathrm{G}@\mathrm{k}$计算如下：$\frac{1}{{\mathrm{l}\mathrm{o}\mathrm{g}}_2(ran{k}_u+1)}$。如果$ran{k}_u>k$，则$\mathrm{N}\mathrm{D}\mathrm{C}\mathrm{G}@\mathrm{k}$为0。对于排名项目，我们为每个基本事实项目考虑100个负样本。对于$k$值，我们选择5和10。

4.3 基线

  为了显示模型的有效性，我们将ASLI与两组推荐基线进行了比较。第一组包含一般的非序列推荐模型：

• MostPop: 一个简单的基线，它根据项目的受欢迎程度对项目进行排名。
• BPR-MF: 贝叶斯个性化排名使用排名损失来分解用户项目交互矩阵[17]。

  第二组包含两个最近提出的序列深度学习模型：

• NextItRec: 这是[24]中提出的下一项推荐的卷积模型。NextItRec使用一维扩展卷积网络来获得过去L个项目的上下文。
• SASRec: 这是一个基于自注意力的序列模型，用于下一项推荐[13]。

  由于其他序列模型(如FPMC[18]、Fossil[8]、改进的GRU4Rec[10]、CASER[20])已被上述序贯模型超越，我们省略与它们的比较。

4.4 实施细节

  我们在TensorFlow中实现了我们提出的模型，并在一个GPU(NVIDIA 1080)上进行了所有的实验。我们使用ADAM优化器[14]来更新模型参数。基于每个用户的平均操作次数，我们将Etsy的最大序列长度定为50，天猫-Small的最大序列长度为100，天猫的最大序列长度为300。NextItRec的批处理大小为32，其余的批处理大小为128。对于所有的模型，200个潜在维度都得到了令人满意的结果。为了调整其他特定于模型的超参数，我们遵循方法作者建议的策略。对于我们的模型，我们从$\{0.1，0.2，0.3，0.4，0.5\}$执行网格搜索后，将dropout设置为0.3，将学习率从$\{0.1，0.01，0.001，0.0001，0.00001\}$设置为0.001。我们还调优了TCN层的内核大小，这将在后面讨论。

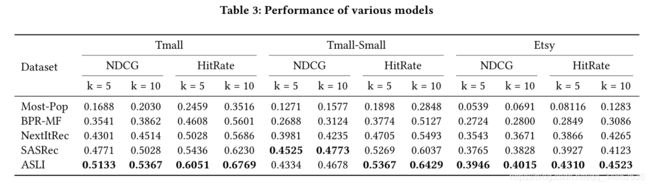
4.5 表现

  为了回答RQ1，我们在表3中报告了每个模型的性能。从表中，我们的第一个观察结果是所有连续深度学习模型组的表现都优于非连续组。在第一组的两个基线模型中，BPR-MF的表现明显好于基于受欢迎程度的模型MostPop。虽然BPR-MF可以学习静态的用户偏好，但它不能捕获序列动态。因此，所有能够学习这种动态的深序列模型的性能都优于BPR-MF。在序列模型中，我们可以观察到，NextItRec在短序列数据(Etsy)上的表现一般要好于长序列数据(无论是天猫还是天猫-Small)。此外，与基于自我注意的模型SASRec相比，Etsy获得了更高的命中率@20(0.4265比0.4123)。据推测，这要归功于NextItRec中扩展内核的固定大小，这使得它能够更好地捕获短长度序列的序列模式，而不是较长序列的序列模式。除此之外，SASRec的表现总体上要好于NexItRec。总体而言，ASLI在所有指标下都取得了最好的性能，除了天猫-Small在NDCG下的性能比SASRec差(k=5时NDCG大约低4%，k=10时大约低2%)。这个结果显示了我们的模型对类别数量的一个最重要的依赖关系。使用只有一个类别的数据集的示例可以更好地解释这种依赖关系。在这种情况下，我们的模型将几乎平等地对待所有类别操作，因此，它将不能完全提取用于发现意图的有用模式。这个例子，无论多么简单，都为解释天猫小数据集的性能差距提供了直观的推理。值得注意的是，天猫-Small是使用Etsy的方案进行预处理的，这个数据集只有130个类别，这可能是NDCG中性能下降的原因。在天猫和Etsy数据集中，分类数都要高得多(超过500个)，并且我们的模型在所有度量下都取得了最好的性能。例如，在NDCG下，这两个数据集的改善至少为4.8%。在击球率下，这是**6%**或更多。接下来，我们讨论了不同注意力的影响，以及核大小$l$对回答RQ2的影响。

4.6 注意力对潜在意图的影响

  为了选择对最后一个注意力层的查询，除了潜在意图之外，我们还可以潜在地使用项、动作或类别的嵌入。表4比较了这些查询选择。这里，‘Seq’表示从第一自注意力层输出的序列。SASRec尝试从第一层查找项目的内在属性，并使用“Seq-Seq”注意力来解析第一层中遗漏的任何依赖项。“Seq-Item”表示使用项嵌入作为第二层中的查询。SEQ-Item的性能比SeqSeq差，可能是因为它冗余地计算项目与序列的相似度，并且可能会丢失第一层中发现的相似度。当使用动作或类别时，性能显著提高，表明两者都是重要因素，因此将两者用作发现潜在意图并关注它的交互会产生更好的推荐。

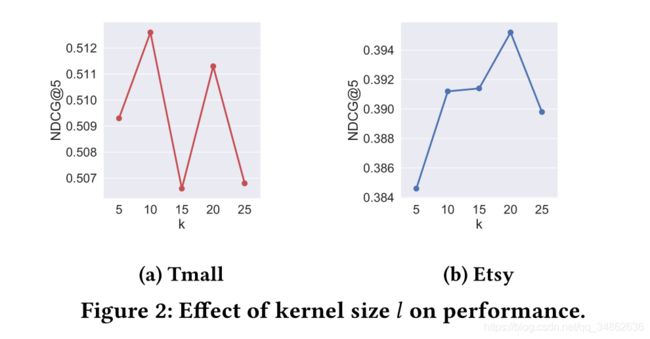
4.7 核大小 $l$ 对性能的影响

  在我们的模型中，TCN层的核大小 $l$ 是一个关键的超参数。为了分析其效果，我们将其大小从5变化到25(间隔为5)，并在图2中的两个数据集显示NDCG@5。如果我们增加l，我们将使用更大的上下文大小来提取潜在意图，这可能会导致性能提高。有趣的是，从图中我们发现，任意增加 $l$ 可能不会带来更好的性能。在我们的例子中，10和20的内核大小在天猫和Etsy上运行得更好。下面讨论回答RQ3的实验结果。

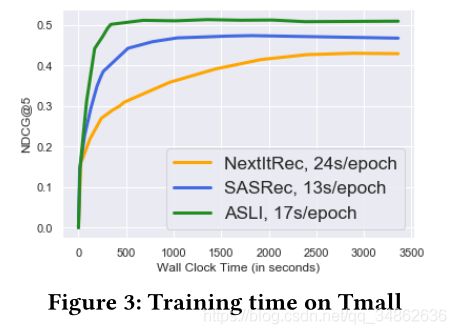
4.8 训练效率和可扩展性

  为了实证地展示我们模型的训练效率，我们测试了我们的模型与其他序列模型相比的收敛速度。图3显示了天猫数据集的收敛结果。我们看到，虽然ASLI的每个epoch时间比SASRec快，但它比其他两个算法收敛得更快(在20个epoch内或大约350秒内)。我们认为这主要是因为我们对下一个项目和下一个交互的联合优化有助于模型快速了解项目之间的关系。在可伸缩性方面，我们应该注意到我们的模型的总体计算复杂度是$\mathcal{O}(n^{2}d+ndl+n{d}^2)$(由自注意力、TCN和FFN层得到)。由于$n$通常较大，所以复杂度由$n^{2}d$项主导。然而，自注意力和TCN层在GPU中都是完全可并行的，并且可以很容易地进行扩展。例如，当我们将天猫的$n$从50增加到600时，每个epoch的时间从7秒增加到45秒。(为简洁起见，未显示完整结果)。

5 相关工作

  传统的推荐系统通过交互矩阵关注用户和项目。这些交互可以是显式的(例如，评级)，也可以是隐式的(例如，点击、购买、评论等)[12，17]。流行的方法包括矩阵分解(MF)方法，该方法旨在从交互矩阵中发现潜在维度[15，19]。由于对“未观察到的”数据(即，用户未与之交互的项)的解释不明确，因此对隐含行为进行建模是具有挑战性的。为了解决这个问题，已经提出了逐点[12]和成对[17]的方法。
  推荐可以通过考虑时间动态来改进。例如，TimeSVD++[2]通过将时间分成几个部分，并在每个部分中分别对用户和项目进行建模，从而在Netflix挑战中取得了很好的结果。这样的模型对于理解表现出时间“漂移”的数据集至关重要[2，23]。
  序列推荐(或下一项推荐)与时态推荐略有不同，因为它只考虑动作的顺序，而不考虑时间戳。FPMC使用矩阵因式分解，并增加了项-项转换项来捕捉长期偏好和短期转换[18]。由于前一项为下一步操作提供了“上下文”，基于第一阶MC的方法表现出很强的性能，特别是在稀疏数据集上[7]。
  一些方法采用高阶MC，它考虑了更多先前的项[6]、[8]。例如，GRU4Rec使用门控循环单元(GRU)对基于会话的推荐的点击序列进行建模[11]，改进后的版本进一步提高了其Top-N推荐性能[10]。在每个时间步长中，RNN将上一步的状态和当前动作作为其输入。这些依赖关系降低了RNN的效率，尽管已经提出了诸如“会话并行”之类的技术来提高效率[11]。卷积网络最近已被应用于顺序推荐设置。CASER[20]将L个前一项的嵌入矩阵视为“图像”，并应用卷积运算来提取过渡，而NextItRec[24]则应用一维膨胀卷积来获得上下文。基于自我注意的[13，25]网络也因其在各种NLP任务中的巨大成功而被提出用于顺序推荐。最近，[22]提出了一种混合通道目的路由网络来模拟匿名会话中物品的不同目的。虽然这些方法可以对动态用户偏好或项目目的进行建模，但它们没有考虑用户意图的影响。我们将推荐视为一项联合任务，即预测下一次交互和下一项，目标是通过一个统一的框架对两者进行建模，以发现用户的潜在意图。

总结

  在本文中，我们提出了ASLI，它通过从用户的交互中捕获用户隐藏的意图来获得更好的推荐。除了发现条目之间的相似性外，ASLI还利用TCN层获得用户意图的潜在表示，用于查询注意力层以发现哪些条目与用户意图最相关。通过实验，我们发现我们的模型在两个真实世界的数据集上的性能要优于目前最先进的模型。