关联规则挖掘 Apriori算法

Apriori算法原理实例解释及python程序

先说两个定律

Apriori定律1：如果一个集合是频繁项集，则它的所有子集都是频繁项集。

举个栗子：假设一个集合{A,B}是频繁项集，即A、B同时出现在一条记录的次数大于等于最小支持度min_support，则它的子集{A},{B}出现次数必定大于等于min_support，即它的子集都是频繁项集。

Apriori定律2：如果一个集合不是频繁项集，则它的所有超集都不是频繁项集。

举个栗子：假设集合{A}不是频繁项集，即A出现的次数小于 min_support，则它的任何超集如{A,B}出现的次数必定小于min_support，因此其超集必定也不是频繁项集。

定律2是定律1的逆否命题，用于构建频繁项集过程中的剪枝操作

上栗子

下面这个表格是代表一个事务数据库D，
其中最小支持度为50%，最小置信度为70%，求事务数据库中的频繁关联规则。

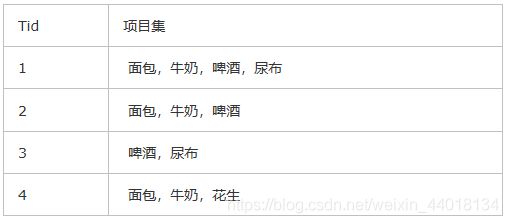
apriori算法的步骤如下所示:
　　(1) 生成候选频繁1-项目集C1={{面包}，{牛奶}，{啤酒}，{花生}，{尿布}}。
　　(2) 扫描事务数据库D，计算C1中每个项目集在D中的支持度。从事务数据库D中可以得出每个项目集的支持数分别为3,3,3,1,2，事务数据库D的项目集总数为4，因此可得出C1中每个项目集的支持度分别为75%，75%，75%，25%，50%。根据最小支持度为50%，可以得出频繁1-项目集L1={{面包}，{牛奶}，{啤酒}，{尿布}}。（实际上删掉支持度低的也是因为其超集也不可能是频繁项，契合定律2）
　　(3) 根据L1生成候选频繁2-项目集C2={{面包，牛奶}，{面包，啤酒}，{面包，尿布}，{牛奶，啤酒}，{牛奶，尿布}，{啤酒，尿布}}。
　　(4) 扫描事务数据库D，计算C2中每个项目集在D中的支持度。从事务数据库D中可以得出每个项目集的支持数分别为3,2,1,2,1,2，事务数据库D的项目集总数为4，因此可得出C2中每个项目集的支持度分别为75%，50%，25%，50%，25%，50%。根据最小支持度为50%，可以得出频繁2-项目集L2={{面包，牛奶}，{面包，啤酒}，{牛奶，啤酒}，{啤酒，尿布}}。
　　(5) 根据L2生成候选频繁3-项目集C3={{面包，牛奶，啤酒}，{面包，牛奶，尿布}，{面包，啤酒，尿布}，{牛奶，啤酒，尿布}}，由于C3中项目集{面包，牛奶，尿布}中的一个子集{牛奶，尿布}是L2中不存在的，因此可以去除（定律2）。同理项目集{面包，啤酒，尿布}、{牛奶，啤酒，尿布}也可去除。因此C3={面包，牛奶，啤酒}。
　　(6) 扫描事务数据库D，计算C3中每个项目集在D中的支持度。从事务数据库D中可以得出每个项目集的支持数分别为2，事务数据库D的项目集总数为4，因此可得出C2中每个项目集的支持度分别为50%。根据最小支持度为50%，可以得出频繁3-项目集L3={{面包，牛奶，啤酒}}。
　　(7) L=L1UL2UL3={{面包}，{牛奶}，{啤酒}，{尿布}，{面包，牛奶}，{面包，啤酒}，{牛奶，啤酒}，{啤酒，尿布}，{面包，牛奶，啤酒}}。
　　(8) 我们只考虑项目集长度大于1的项目集（这里寻找的是真子集，1对1的关联规则会在频繁2项集的真子集中获得），例如{面包，牛奶，啤酒}，它的所有真子集{面包}，{牛奶}，{啤酒}，{面包，牛奶}，{面包，啤酒}，{牛奶，啤酒}，分别计算关联规则{面包}—>{牛奶，啤酒}，{牛奶}—>{面包，啤酒}，{啤酒}—>{面包，牛奶}，{面包，牛奶}—>{啤酒}，{面包，啤酒}—>{牛奶}，{牛奶，啤酒}—>{面包}的置信度，其值分别为67%，67%，67%，67%，100%，100%。由于最小置信度为70%，可得}，{面包，啤酒}—>{牛奶}，{牛奶，啤酒}—>{面包}为频繁关联规则。也就是说买面包和啤酒的同时肯定会买牛奶，买牛奶和啤酒的同时也是会买面包。L中剩下的频繁项集用相同的方式进行处理

上程序

数据要求

执行部分里修改文件路径， csv文件输入，第一列为事务列，第二列及以后为项集列

参数调节

可调参数：执行部分里的k=2, min_support=0.01，min_conf=0.15可调节，并有说明

import time
import csv
def readData(fileName):#数据导入
    """
    将csv文件数据转化为list of list格式
    :param fileName:
    :return: a list, as form as [[items list],[items list]...]
    """
    with open(fileName) as csvFile:
        reader = csv.reader(csvFile)
        transactions = []
        for line in reader:
            ID = line[0]
            itemList = []
            for item in line[1:]:
                if item=='':
                    break                
                itemList.append(item)
            transactions.append(itemList)
    return transactions
 def create_C1(data_set):#创建频繁一项集
    C1 = set()
    for t in data_set:
        for item in t:
            item_set = frozenset([item])#将单个产品类型放入不可变集合
            C1.add(item_set)
    return C1
 def is_apriori(Ck_item, Lksub1):
    for item in Ck_item:
        sub_Ck = Ck_item - frozenset([item])
        if sub_Ck not in Lksub1:
            return False
    return True
 def create_Ck(Lksub1, k):#频繁k项集创建
    Ck = set()
    len_Lksub1 = len(Lksub1)
    list_Lksub1 = list(Lksub1)
    for i in range(len_Lksub1):
        for j in range(1, len_Lksub1):
            l1 = list(list_Lksub1[i])
            l2 = list(list_Lksub1[j])
            l1.sort()
            l2.sort()
            if l1[0:k-2] == l2[0:k-2]:
                Ck_item = list_Lksub1[i] | list_Lksub1[j]
                # pruning
                if is_apriori(Ck_item, Lksub1):
                    Ck.add(Ck_item)
    return Ck
 def generate_Lk_by_Ck(data_set, Ck, min_support, support_data):
    Lk = set()
    item_count = {}
    for t in data_set:
        for item in Ck:
            if item.issubset(t):
                if item not in item_count:
                    item_count[item] = 1
                else:
                    item_count[item] += 1
    t_num = float(len(data_set))
    for item in item_count:
        if (item_count[item] / t_num) >= min_support:
            Lk.add(item)
            support_data[item] = item_count[item] / t_num
    return Lk
 def generate_L(data_set, k, min_support):
    support_data = {}
    C1 = create_C1(data_set)
    L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
    Lksub1 = L1.copy()
    L = []
    L.append(Lksub1)
    for i in range(2, k+1):
        Ci = create_Ck(Lksub1, i)
        Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
        Lksub1 = Li.copy()
        L.append(Lksub1)
    return L, support_data
def generate_big_rules(L, support_data, min_conf):
    big_rule_list = []
    sub_set_list = []
    for i in range(0, len(L)):
        for freq_set in L[i]:
            for sub_set in sub_set_list:
                if sub_set.issubset(freq_set):
                    conf = support_data[freq_set] / support_data[freq_set - sub_set]
                    big_rule = (freq_set - sub_set, sub_set, conf)
                    if conf >= min_conf and big_rule not in big_rule_list:
                        # print freq_set-sub_set, " => ", sub_set, "conf: ", conf
                        big_rule_list.append(big_rule)
            sub_set_list.append(freq_set)
    return big_rule_list
 if __name__ == "__main__":
    start = time.time()
    #data_set = load_data_set()
    #数据导入
    filename='test.csv'
    data_set=readData(filename)
    #设置最小支持度，表示某规则在整体数据库中的占比，取值可小一点；K表示K项集，即候选的每个关联规则中最多涉及几个产品
    L, support_data = generate_L(data_set, k=2, min_support=0.01)
    #设置最小置信度，表示的是关联规则中一个出现的情况下，另一个出现的概率，可以适当大一些
    big_rules_list = generate_big_rules(L, support_data, min_conf=0.15)
    for Lk in L:
        print ("="*50)
        print ("frequent " + str(len(list(Lk)[0])) + "-itemsets（频繁项集）\t\tsupport（支持度）")
        print ("="*50)
        for freq_set in Lk:
            print (freq_set, support_data[freq_set])
    print ("强关联")
    for item in big_rules_list:
        print (item[0], "=>", item[1], "conf(置信度): ", item[2])
    end=time.time()
    print('运行时间：',str(end-start))

附加一点：上面这个支持csv，数据量过大时一般为txt存储，下面这个是处理txt，将txt文件转化为list of list,只贴处理txt文件的程序，txt的列和上面csv保持一致

def loadDatadet(infile):  #读TXT文件转化为list of list  
    f=open(infile,'r',encoding='utf-8')    
    sourceInLine=f.readlines()    
    dataset=[]
    for line in sourceInLine:        
        temp1=line.strip('\n')
        temp2=temp1.split('\t')
        temp=temp2[1].split()
        dataset.append(temp)     
    return dataset