时间序列分析应用实例（使用Eviews软件实现）

引言
某公司的苹果来货量数据是以时间先后为顺序记录的一组数据，从计量经济学的角度来分类就是一组时间序列数据。为了提高苹果来货量预测的准确度以及预测结果的可信度，下面运用Eviews软件包（即Econometrics Views 计量经济学软件包）并结合计量经济学的理论知识，选取2017年1月至2019年4月的苹果来货量月度数据（事前对原始数据进行处理，把数值单位从吨转换为万吨）为样本数据，用一个时间序列模型来拟合上述样本数据，然后利用建立好的模型预测苹果未来几个月的来货量情况，并对预测结果进行分析。

1 平稳性检验

1.1 初步检验

设来货量时间序列为Qt，首先观察Qt的折线图，如图1所示：

图1 Qt的折线图

从图1可知，苹果来货量的月度数据总体呈下降趋势，并存在季节性因素，进而通过序列原水平的自相关系数图进一步探讨序列的平稳性，结果如图2所示：

图2 Qt的自相关系数图

从图2可以看到，所有的自相关系数（Autocorrelation）均落在2倍标准差之内（垂立的两道虚线表示2倍标准差），初步判定序列Qt是平稳的。下面运用ADF单位根检验法证明序列的平稳性。

1.2 ADF单位根检验
假设序列Qt的特征方程存在多个特征根，那么序列平稳的条件为所有特征根λi的绝对值均小于1，即所有特征根都在单位圆内。构造该ADF检验的原假设H0：存在i，使得λi＞1，备择假设H1：λ1, λ2, … , λp＜1，运用Eviews软件对序列Qt的原水平进行带常数项（Intercept）的ADF检验，采用SC准则自动选择滞后阶数，检验结果如图3所示：

图3 ADF检验

根据图3的检验结果可知，t统计量（t-Statistic）的伴随概率p为0.00，在显著性水平α=0.05下，因此我们有理由拒绝原假设（p＜α），说明序列Qt是平稳的。

2 模型识别

从图2可知，序列Qt的自相关系数（Autocorrelation）和偏自相关系数（Partial correlation）均在阶数1处突然衰减为在零附近小值波动，因此我们初步选择AR(1)、ARMA(1,1)这两个模型拟合样本数据

3 模型参数估计

3.1 AR(1)模型的拟合与参数估计

设AR(1)模型为：Qt=C + Φ*Qt-1 +εt，其中C为常数项，Φ为待估计的Qt滞后一阶的系数，εt为服从均值为零、方差为常数正态分布的正态分布（即白噪声序列），下面运用Eviews软件对AR(1)模型的参数采用最小二乘估计法（无偏估计）进行参数估计，模型估计结果如图4所示：

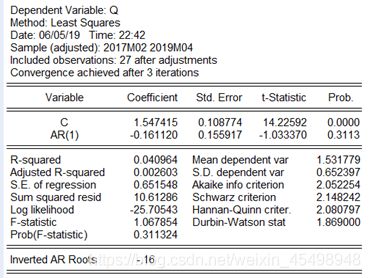
图4 AR(1)模型拟合结果

根据图4的参数估计结果来看，在显著性水平α=0.05下，常数项显著不为零，而参数Φ的显著性估计结果并不是太好，另外AR(1)模型的特征方程的根（Inverted AR Roots）为-0.16，印证了序列Qt是平稳的。AR(1)模型的拟合结果如下:

  Qt=1.547415 - 0.161120 Qt-1 +εt

3.2 AR(1)模型的残差序列的独立性检验（Residual Diagnostics）
我们希望运用样本数据拟合AR(1)模型的残差序列是一个白噪声序列，即残差序列各项是相互独立的，模型的拟合结果不由残差序列来解释。AR(1)模型拟合后的残差序列的独立性检验结果如图5所示：

图5 AR(1)残差序列自相关系数图

根据图5的检验结果来看，在显著性水平α=0.05下，我们没有充分的理由拒绝残差序列为白噪声的原假设，即AR(1)模型通过残差独立性的检验。

3.3 ARMA(1,1)模型的拟合与参数估计

设ARMA(1,1)模型为：Qt=C + ΦQt-1 +εt +θεt-1，其中C为常数项，Φ为待估计的Qt滞后一阶的系数，θ为待估计的εt滞后一阶的参数，εt为均值为零、方差为常数的白噪声序列。下面运用Eviews软件对ARMA(1,1)模型的参数采用最小二乘估计法（无偏估计）进行参数估计，模型估计结果如图6所示：

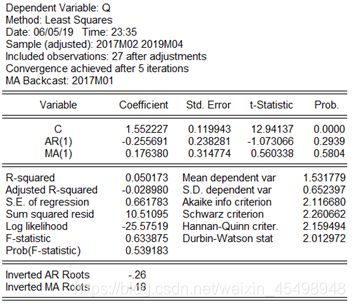
图6 ARMA(1,1)模型拟合结果

根据图6的参数估计结果来看，在显著性水平α=0.05下，只有常数项显著不为零，而参数Φ和θ的显著性估计结果并不是太好，而ARMA(1,1)模型的模型的特征方程的根均在单位圆内，印证了序列Qt是平稳的。ARMA(1,1)模型的拟合结果如下:

Qt=1.552227– 0.255691Qt-1 +εt + 0.176380εt-1

3.4 ARMA(1,1)模型的残差序列的独立性检验（Residual Diagnostics）

同理，ARMA(1,1)模型拟合后的残差序列的独立性检验结果如图7所示：

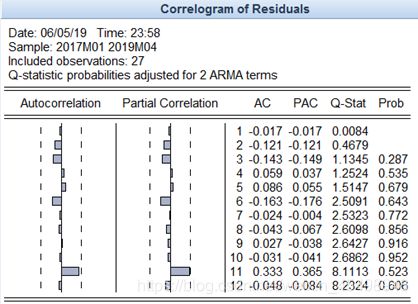
图7 ARMA(1,1)模型的残差序列自相关系数图

根据图7的检验结果来看，在显著性水平α=0.05下，我们没有充分的理由拒绝残差序列为白噪声的原假设，即ARMA(1,1)模型通过残差独立性的检验。

4 模型比较及选择

对于模型的比较与选择，往往不是简单看某一个指标，而是综合考虑各方面的情况，作出一个综合的判断，选择一个最优模型。一般考虑以下几个因素：

（1）R-squared（R方）、Adjusted R-squared（调整R方），这两个指标应该是越大越好。当两个指标较大时，说明所拟合的模型较好地提取了数据中的信息。

（2）模型拟合中的各参数估计情况是否显著地非零。一般来说，可以通过参数估计的t统计量对应的伴随概率Prob. 项是否显著地小于给定的显著性水平α（一般α取0.05）。

（3）AIC及SBC准则，也就是Akaike info criterion 项及Schwarz criterion项，一般来说，这两项指标应该是越小越好。

（4）DW值，应该看该值是否接近2.也就是Durbin-Watson stat项，这一指标代表的是模型拟合后的残差序列是否存在一阶自相关关系。如果残差序列中存在一阶自相关关系，说明模型的拟合效果不是很理想，在残差序列中还有信息没有充分提取。当DW值接近2时，代表着残差序列不存在自相关关系，模型拟合良好；当DW值接近0时，代表残差序列存在很强的正自相关；当DW值接近4时，代表着残差序列存在很强的负自相关关系。

（5）模型的单位根的绝对值，即系数方程根的倒数的绝对值（Inverted AR Roots与Inverted MA Roots）要小于1，进一步印证可以建立模型的时间序列是平稳的。

（6）需要估计参数的个数。一般来说，需要估计的参数越少越好，比较少的估计可以尽可能地减少估计过程中的偏差。

根据以上几个因素综合考虑，把模型参数估计的显著性水平α上调至0.5，我们最终选择AR(1)模型

5 预测分析
已知AR(1)模型的拟合结果为Qt=1.547415 - 0.161120 Qt-1 +εt，下面根据选择的模型采用动态预测（Dynamic）的方法对未来3个月(即2019.05-2019.07)进行预测，预测结果如图8所示：

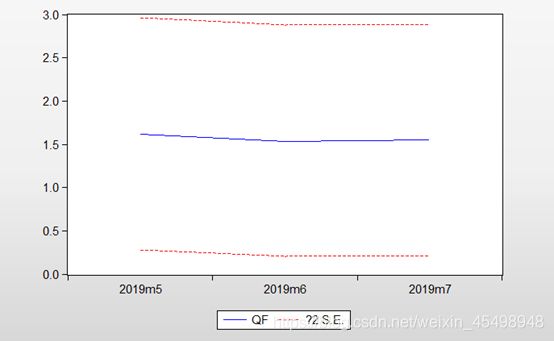
图8 5-7月预测折线图

其中，中间蓝色折线表示预测的理论值，上下两条虚线表示在2倍标准差波动范围内的最大预测值及最小预测值，5月份苹果来货量预测值为1.616608万吨（即16166.08吨），6月份的预测值为1.536267万吨（即15362.67吨），7月份的预测值为1.549212万吨（即15492.12吨）。已知5月份苹果实际来货量为8297.5吨，对比相差7868.58吨，误差为高达48.67%，说明模型需要进一步优化。另一方面，该结果也表明苹果的实际来货量对比预期判断的来货量，下降幅度存在异常，需要后续进一步挖掘和分析。