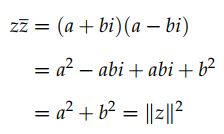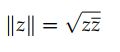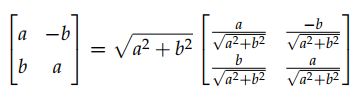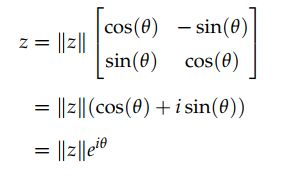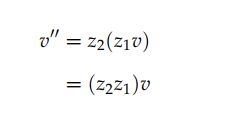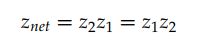复数的相关知识
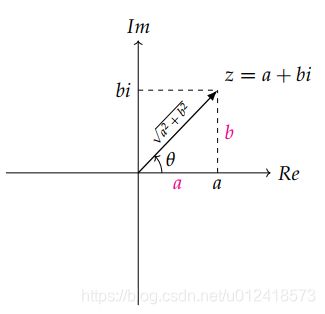
1.任意一个复数 z ∈ C z\in C z∈C都可以表示成 z = a + b i z=a+bi z=a+bi的形式，其中 a , b ∈ R a,b\in R a,b∈R 而且 i 2 = − 1. a i^2=-1. a i2=−1.a为实部（Real Part）, b b b为虚部（Imaginary Part）。
z = a + b i z=a+bi z=a+bi是对于 { 1 , i } \{1,i\} {1,i}这个基（Basis）的线性组合：
2.性质
（1）复数加减法
（2）复数乘法
z 1 z 2 = ( a + b i ) ( c + d i ) = a c + a d i + b c i + b d i 2 = ( a c − b d ) + ( b c + a d ) i z_1z_2=(a+bi)(c+di)=ac+adi+bci+bdi^2=(ac-bd)+(bc+ad)i z1z2=(a+bi)(c+di)=ac+adi+bci+bdi2=(ac−bd)+(bc+ad)i
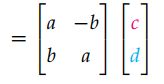
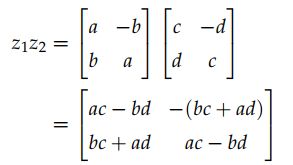
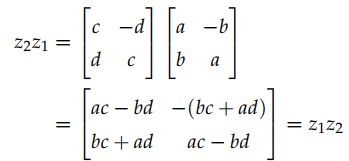
(3)复数的模长与共轭
模长：
共轭：
性质：
3.复数相乘与2D旋转
复数相乘可以写成： z 1 z 2 z_1z_2 z1z2
则变换矩阵可以写成：
复数如何表示2D旋转：
由上边的公式可以看车，复数相乘可以表示成旋转矩阵与复数向量相乘，因此对于基向量 [ 1 , 0 ] T 和 [ 0 , 1 ] T [1,0]^T和[0,1]^T [1,0]T和[0,1]T的变换效果:
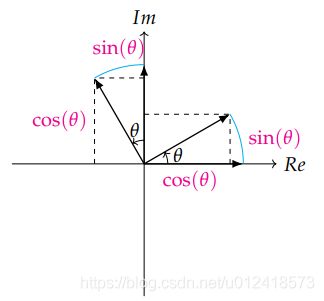
因此，复数相乘其实就是旋转与缩放变换的复合。如果 ∣ ∣ ∣ z ∣ = 1 |||z|=1 ∣∣∣z∣=1，则复数矩阵可以表示成：
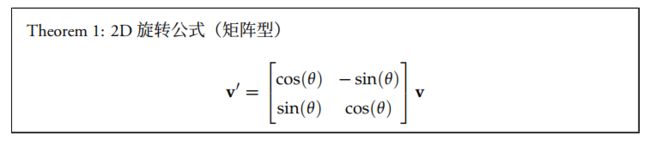
为纯旋转矩阵，没有缩放功能。因此，如果想让2D空间中任意向量 v \bm{v} v旋转 θ \theta θ度，就可以使用定理1的变换公式：
复数的极坐标表示形式：
因此，复数同样可以表示成
4.旋转的复合
结论：当我们对两个2D旋转进行复合时，所得的变换 z n e t z_{net} znet仍然是一个旋转，并且与施加次序无关，旋转角是 z 1 和 z 2 z_1和z_2 z1和z2之和。