Discrete Mathematics 离散数学——图论
Discrete Mathematics 离散数学——图论
- 定理: The Hand Shaking Theorem
- 基本的图
- Complete graph Kn
- Cycles Cn
- Whells Wn
- n-cube Qn
- 二分图:Bipartite Graphs
- 定理:二分图的一种判定
- 完全二分图 Complete bipartite graph
- 匹配(matching)和最大匹配
- Hall's Marriage Theorem
定理: The Hand Shaking Theorem
Hand Shaking Theorem: Let G = (V, E) be an undirected graph with m edges, then
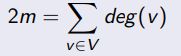
Proof: Each edge contribute twice to the sum of the degrees of vertices, so the sum of the degrees is twice the number of edges.
Corollary of HS Theorem(推论): An undirected graph has an even number of vertices of odd degree.
证明非常简单,因为总的度数是偶数(2m),所以只可能有奇数条边(否则度数出现奇数)
基本的图
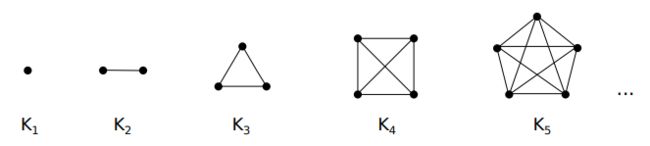
Complete graph Kn
The complete graph is the graph with n vertices and an edge connecting each pair of distinct(不同的) vertices. (n >= 1)
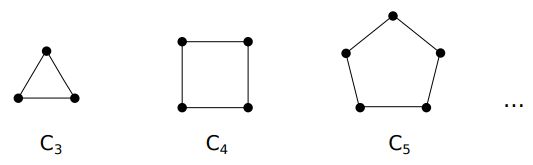
Cycles Cn
Cn is the graph with n vertices v1, v2, … , vn, and edges (v1, v2), (v2, v3), … , (vn, v1) (n >= 3)
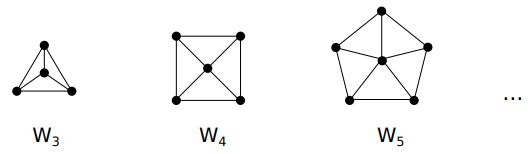
Whells Wn
Obtained from Cn by adding a vertex and connecting it to each vertex of Cn (n >= 3)
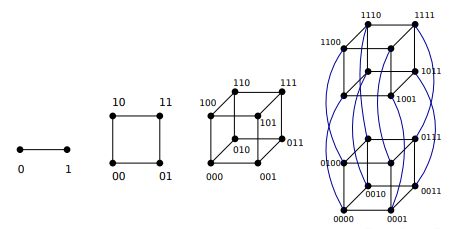
n-cube Qn
The graph with 2^n vertices representing the bit string of length n. Two vertices are connected if the bit string they represent differ by one bit. (n >= 1)
二分图:Bipartite Graphs
满足,V集合()所有点可以被分成两个不相交集,满足图中的每条边都连接一个 V1 中的点和一个 V2 中的点,那这个图是二分图。
定理:二分图的一种判定
定理:一个图是二分的,当且仅当它可以被两种颜色涂满
完全二分图 Complete bipartite graph
定义:如果 A 和 B 分别是 V1,V2 集中的两个点,那么他们之间一定会有连线
表示: K(m, n): m 和 n 是两个集合中的点数
匹配(matching)和最大匹配
一个图中的matching指的是:一个集合 E 的子集 M ,使得没有任何两个边连向同一个节点
Maximum Matching: 有着最多边数的matching
Complete Matching from V1 to V2(从 V1 到 V2 的完全匹配):如果每个 V1 里的节点都是匹配的端点
Hall’s Marriage Theorem
定义(邻居 neighborhood):A 是 E 的子集,那么 N(A) 是相邻于至少一个 A 中节点的节点集合
Hall’s Marriage Theorem: 一个二分图,如果对于所有 V1 的子集 A 而言都有 |N(A)| >= |A|,那么这个二分图有从 V1 到 V2 的完全匹配