机械码补码，阶码的表示与范围思考总结

       对于这个标题我也是无奈之举，实在想不出比较合适的标题，但我想陈述的问题其实很简单——有关二进制机械码范围问题的思考：

       其实主要是补码和浮点数表示中的指数阶码表示范围的一些想法，举个例子，8位二进制补码表示范围为-128到127，而8位浮点数表示中的指数阶码表示为-127到128，这些小问题确实很头疼（尤其对于我这样的IQ不咋地人......）,但好在最后还是想通了......言归正传，先从原反补码说起：

       对于原反补码的最常用解释就是——

          （1）原码——将十进制数真值绝对值转化为二进制，若真值为正，则在对应二进制数前加0，若为负则加1；  

          （2）反码——负数：将十进制数对应的二进数原码除符号位外按位取反，正数：和原码一致；

          （3）补码——负数：将十进制数对应的二进制反码加1，正数：和原码一致；

                                                            以十进制数 -2 为例：

                                                                       原码：110；

                                                                       反码：101；

                                                                       补码：110；

以上的解释是最长用的，但却不能解决以上问题，准确的说，以上解释仅仅是解释而非定义，在白中英教授的《计算机组成原理》中就对这些机械码做了函数上的定义，以补码为例：

   【x】补 =  x , 2^n>x≥0 ;  2^(n+1)+x=2^(n+1)-|x| , 0≥x≥-2^n

而且通过这个定义，有了一个较标准的公式来计算补码到真值的转化：x=-2^n*xn+∑2^i*xi  (i=0 ; i -> n-1)①

这个式子中x为真值，为了解释这个式子，举两个例子：

               T1：已知【x】补=010011011，求x=？

                       解：利用式①，得x = 0*2^8 + 1*2^7 + 0*2^6 + 0*2^5 + 1*2^4 + 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0=155

                故x=155。

               T2：已知【x】补=110011011，求x=？

                      解：利用式①，得x = -1*2^8 + 1*2^7 + 0*2^6 + 0*2^5 + 1*2^4 + 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = -256 + 155 = -101

                故x=-101。

从以上两个例子就不难理解式子 ①了，那么我们可以回归正题了，以n+1位二进制为例：

这张图中就描述了n+1位二进制表示的范围，为了更详细点，以3位二进制数为例，此时n=2：

                               -3                 -2               -1                0                1                  2                   3

原码：                    111               110            101         100/000         001             010               011

反码：                    100               101           110          111/000         001             010               011

补码：    100           101               110           111             000            001              010               011

       神奇的事发生了，多了一个100出来，按上图所示100应该为-2^2也就是-4的补码，但-4的原码为1100，按我们常用的解释求其反码按位取反得到其补码应该是1100，

也就是说-4有两个补码？还是说有一个不对，我们用式①验证一下，对于100，x = -1*2^2 + 0*2^1+ 0*2^0= -4, 对于1100， x= -1*2^3+1*2^2 + 0*2^1+ 0*2^0=-4,所以不难得出结论，这两个都是-4的补码，（这就是为什么我花大量篇幅去解释这个式子的原因）其实还-4的补码还不止这两个，因为-4的原码就有许多个，

       比如10100,100100,1000100，......只要首位为1，末3位位100，中间无论多少个0表示的都是-4的原码，只是我们跟常用1100来表示-4的原码，按照按位取反加1，就可以得到许多个不同位数的补码了，我们所说的补码唯一是在规定二进制码位数的情况下某一个十进制数的补码是唯一的，只是-4的3位二进制补码无法求得其对应的原码而已，这就是为什么本文一开头就强调我们对机械码的表述仅仅是解释而非定义的原因，因为对于-4而言它没有3位下的二进制原码，所以也就无法由解释得到其3位二进制补码，而必须由补码的定义确认，而-4的3位二进制的补码的产生也正是由-0（也就是0）的反码得到的补码，这样0的补码就唯一了，由此推论到n次幂，这就成功解释为什么n+1位补码能多表示一个负数的补码，因为那是0让出来的位置，而它由满足补码定义，故它就是-2^n在n+1位下的补码。

      说完了补码，再说说阶码，阶码是用来表示浮点数指数的编码，其采用的方式为移码表示法，对移码的定义同样也有一个式子，【e】移=2^k + e, （其中e为真值）而阶码所采用的移码则并非加的是2^k,而是加上的2^k-1,为什么要这样处理呢？我们看下图：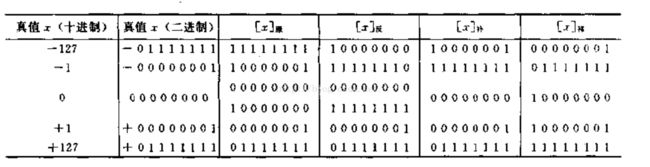

此图所描述的是当k=2时的各机械码表示，最后一行为移码，你发现了吗？00000000这个编码没有用上去，这是因为移动的位数为2^k，而当移动值为2^k-1时，-127所对应的阶码就是00000000了，那么+127就可以用11111110表示了，而11111111则表示的是+128，是不是顿时觉得这种移码表示的阶码很机智啊，成功的在有限位数条件下多表示了一个数，而且用移码表示阶码的优点也得到保存，那就是移码大的数其真值也大，在此就先总结这么多，仅为我的一点想法没若有不正确的地方还请诸位指出，，，在此感谢，，，balalalalala~~~