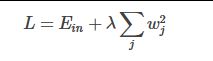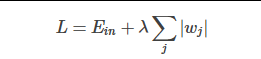4.11网易互娱笔试知识点补充
啥 也 不 会
delete drop remove
SQL的drop,delete,remove,update和truncate之间的区别
delete:删除满足条件的某行/表内所有行
Delete * from table 表名 where……
Delete from table 表名
drop:删除数据表/数据库/数据表字段
删除数据表时 表的结构、属性、索引也会被删除
drop table 数据表1名称,数据表2名称
drop column 字段名(列名称)
remove:删除数据库文件
alter database Mydatabase1
remove file Mydatabase1_log
truncate:删除数据表中的数据
仅删除数据表中的数据 表结构不会被删除
truncate table 数据表名称
Logistic回归模型
模型选择之AIC与BIC
通常选择AIC最小的模型
logistic学习笔记
KNN模型
KNN简介
KNN算法常见问题总结
1、计算测试对象到训练集中每个对象的距离
2、按照距离的远近排序
3、选取与当前测试对象最近的k的训练对象,作为该测试对象的邻居
4、统计这k个邻居的类别频率
5、k个邻居里频率最高的类别,即为测试对象的类别
随机函数
python--随机函数(random,uniform,randint,randrange,shuffle,sample)
random.uniform(a,b):用于生成一个指定范围内的随机浮点数
两个参数中,其中一个是上限,一个是下限。如果a>b,则生成的随机数n,即b<=n<=a;如果a>b,则a<=n<=b
Bagging&Boosting
Bagging和Boosting的区别
| bagging | boosting |
| 训练集有放回选取 | 训练集不变 |
| 样例的权重相等 | 样例的权重变化 |
| 预测函数的权重相等 | 预测函数的权重变化 |
| 预测函数可以并行生成 | 预测函数只能顺序生成 |
| 减少variance | 减少bias |
三引号
python单引号(')、双引号(")、三引号(''',""")
python中的单引号双引号和三引号
三单引号可以直接打印多行内容 而单引号和双引号需要\n才能换行
基尼指数
基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
在样本集合中一个随机选中的样本被分错的概率
基尼系数的性质与信息熵一样:度量随机变量的不确定度的大小;
G 越大,数据的不确定性越高;
G 越小,数据的不确定性越低;
G = 0,数据集中的所有样本都是同一类别
模型评价
准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F值(F-Measure)、AUC、ROC的理解
准确率、精确率、召回率、F1值、ROC/AUC整理笔记
准确率/正确率 = 所有预测正确的样本/总的样本
精确率/查准率 = 正确预测为正的占全部预测为正的比例
召回率/查全率 = 即正确预测为正的占全部实际为正的比例
F值 = 精确率 * 召回率 * 2 / ( 精确率 + 召回率) (F 值即为精确率和召回率的调和平均值)
ROC曲线越靠拢(0,1)点,越偏离45度对角线越好
AUC值越大的分类器,正确率越高
正则化
【通俗易懂】机器学习中 L1 和 L2 正则化的直观解释
L1、L2正则化知识详解
L1正则化和L2正则化
L2 正则化公式:直接在原来的损失函数基础上加上权重参数的平方和
L1正则化公式:直接在原来的损失函数基础上加上权重参数的绝对值
L2正则化的效果是对原最优解的每个元素进行不同比例的放缩
L1正则化则会使原最优解的元素产生不同量的偏移,并使某些元素为0,从而产生稀疏性
结构风险最小化:在经验风险最小化(训练误差最小化)的基础上,尽可能采用简单的模型,以提高模型泛化预测精度
范数
机器学习中的范数规则化之(一)L0、L1与L2范数
L0、L1、L2范数在机器学习中的应用
L0范数是指向量中非0的元素的个数
L1范数是指向量中各个元素绝对值之和
L2范数是指向量各元素的平方和然后求平方根
L0范数很难优化求解(NP难问题)&L1范数是L0范数的最优凸近似,比L0范数要容易优化求解
typeⅠ typeⅡ错误
《概率论与数理统计》之 typeⅠ、typeⅡ(第一类错误和第二类错误)理解
H0:A!=B H1:A=B
第一类错误:H0实际上成立 但拒绝了这一假设 在A!=B的情况下认为A=B 真当假
第二类错误:H0实际上不成立 但接受了这一假设 在A=B的情况下认为A!=B 假当真