hdu1667-IDA*-迭代加深搜索 A*算法

迭代加深搜索

迭代加深搜索，实质上是限定下界的深度优先搜索。即首先允许深度优先搜索K层，若没有发现可行解，再将K+1后重复以上步骤搜索（即深度优先搜索k+1层），直到搜索到可行解。

在迭代加深搜索的算法中，连续的深度优先搜索被引入，每一个深度约束逐次加1，直到搜索到目标为止。可以看出，很多情况会重复搜索。但是它的好处在于：

1. 空间开销小。每个深度下实际上是一个有深度限制的深度优先搜索。而DFS的空间消耗小是众所周知的。
2. 利于深度剪枝。
3. 时间效率不低。虽然重复搜索，但是整体并不比广度有限搜索慢很多。

我们可以看出，迭代加深搜索算法就是仿广度优先搜索的深度优先搜索。既能满足深度优先搜索的线性存储要求，又能保证发现一个最小深度的目标结点。

从实际应用来看，迭代加深搜索的效果比较好，并不比广度优先搜索慢很多，但是空间复杂度却与深度优先搜索相同，比广度优先搜索小很多。

使用搜索算法的时候，选择正确的搜索方式很重要。当有一类问题需要做广度优先搜索，但却没有足够的空间，而时间却很充裕，碰到这类问题，我们可以选择迭代加深搜索算法。

一般来说，如果目标结点离根结点远，需要遍历整棵树，可以考虑使用深度优先搜索；如果目标离根结点近，或求最小步数，则考虑广度优先搜索或迭代加深搜索；若广度优先搜索存在空间不够的问题，则考虑使用迭代加深搜索。

A*

A*算法我现在也不是很懂，就不说了，免得误导大家。可以自己google一下，有点了解后就可以看这题了。感觉这题是迭代加深搜索的模板题，只不过用了一点A*的思想。

HDU1667

上面的看一遍没看懂没关系，先看看题目，把代码看懂了再看上面的解释就好懂了。
我搜这一题的博客搜了好多，基本都没有详细一点的讲解，直接贴的代码。不过后来发现一个博客讲的很好，还好看到他的博客，不然真没学到什么。自觉这个博客已经讲的很详细很好了，我就直接转载了。
转载自：https://lo-li.net/1363.html#comment-737

问题描述

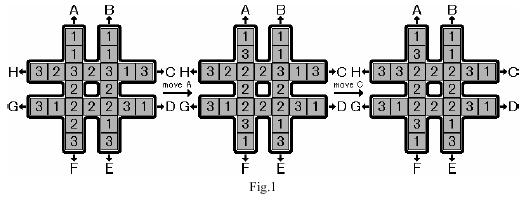
现有一块有24个格子的井字板子，每个格子用1、2或3标记，每种格子各有8个。
起初这些格子分布随机，你需要通过A-H 8种操作将中心8个格子作变为相同的标记。（图中使用A操作将A列向上拉了一格，C操作将C列向右拉了一列，中心变为2）

输入

有多组数据(≤30)，每组数据包含一行24个数字，代表从左上到右下24个格子的初始状态。输入0代表结束。

输出

每组数据包含两行，第一行是最佳的操作顺序，第二行是此时中心的字符。若不需要操作，即初始时中心八个字符就相同，则输出No moves needed。（也要输出中心字符）
最佳操作顺序为：操作次数最少，同次数若有多种则为字典序小者

将板子如上图编号存下来，操作A-H编号为0-7

#include 
using namespace std;

const int center[] = {6,7,8,11,12,15,16,17};  //中心8个点坐标
const int reverseop[] = {5,4,7,6,1,0,3,2,-1};  //每种操作的逆操作
const int index[8][7] = {  //从A-H操作变动的下标
    { 0,2,6,11,15,20,22 },    //A
    { 1,3,8,12,17,21,23 },    //B
    { 10,9,8,7,6,5,4 },       //C
    { 19,18,17,16,15,14,13 }, //D
    { 23,21,17,12,8,3,1 },    //E
    { 22,20,15,11,6,2,0 },    //F 
    { 13,14,15,16,17,18,19 }, //G
    { 4,5,6,7,8,9,10 },       //H
};
int mp[24];
char finop[105];  //搜到目标的操作序列
bool flag;  //是否搜到目标

执行某一个操作只需将那一列/行每格顺序往后挪

void option(int op)
{
    int tmp=mp[index[op][0]];
    for(int i=0;i<6;i++)
    {
        mp[index[op][i]] = mp[index[op][i+1]];
    }
    mp[index[op][6]]=tmp;
}

估值函数，找出当前局面下使得中心点变成1、2和3所需的最小步数。因为总共就3个数，一次任何一种操作只会改变中间一种数字的数量，用8减去数量最多那个数字的个数即为最小步数。

int get_h()
{
    int cnt[3]={0};
    int num=-1;
    for(int i=0;i<8;i++)
    {
        cnt[mp[center[i]]-1]++;
        num = max(num,cnt[mp[center[i]]-1]);
    }
    return 8-num;
}

搜索

迭代加深：保证第一次搜到的解是最短的

从A操作到H操作搜，保证字典序最小

可行性剪枝：当前深度（已操作的次数）+估价函数值= （至少还需要的步数）若大于当前规定的最大深度（最多步数）则剪枝

相邻操作不为互逆操作

void dfs(int depth,int lastop,int maxdepth)  //depth当前深度 lastop上一次的操作 maxdepth每次迭代加深搜索的最大深度
{
    if(flag) return;
    if(depth>maxdepth || depth+get_h()>maxdepth) return;  //可行性剪枝
    if(get_h()==0)  //中心相同了
    {
        flag=true;
        finop[depth]='\0';
        printf("%s\n%d\n",finop,mp[center[0]]);
        return;
    }
    for(int nextop=0;nextop<8;nextop++)  //从A开始搜索
    {
        if(nextop!=reverseop[lastop])  //与上一次操作不互逆
        {
            option(nextop);
            finop[depth]=nextop+'A';
            dfs(depth+1,nextop,maxdepth);
            option(reverseop[nextop]);  //回溯还原
        }
    }
}

int main()
{
    while(1)
    {
        for(int i=0;i<24;i++)
        {
            scanf("%d",&mp[i]);
            if(mp[i]==0) return 0;
        }
        if(get_h()==0)
        {
            printf("No moves needed\n%d\n", mp[center[0]]);
            continue;
        }
        flag=false;
        for(int depth=1;!flag;depth++) //迭代加深
        {
            dfs(0,8,depth);
        }
    }
    return 0;
}

完整代码

#include 
using namespace std;

const int center[] = {6,7,8,11,12,15,16,17};  //中心8个点坐标
const int reverseop[] = {5,4,7,6,1,0,3,2,-1};  //每种操作的逆操作
const int index[8][7] = {  //从A-H操作变动的下标
    { 0,2,6,11,15,20,22 },    //A
    { 1,3,8,12,17,21,23 },    //B
    { 10,9,8,7,6,5,4 },       //C
    { 19,18,17,16,15,14,13 }, //D
    { 23,21,17,12,8,3,1 },    //E
    { 22,20,15,11,6,2,0 },    //F 
    { 13,14,15,16,17,18,19 }, //G
    { 4,5,6,7,8,9,10 },       //H
};
int mp[24];
char finop[105];  //搜到目标的操作序列
bool flag;  //是否搜到目标

int get_h()
{
    int cnt[3]={0};
    int num=-1;
    for(int i=0;i<8;i++)
    {
        cnt[mp[center[i]]-1]++;
        num = max(num,cnt[mp[center[i]]-1]);
    }
    return 8-num;
}

void option(int op)
{
    int tmp=mp[index[op][0]];
    for(int i=0;i<6;i++)
    {
        mp[index[op][i]] = mp[index[op][i+1]];
    }
    mp[index[op][6]]=tmp;
}

void dfs(int depth,int lastop,int maxdepth)  //depth当前深度 lastop上一次的操作 maxdepth每次迭代加深搜索的最大深度
{
    if(flag) return;
    if(depth>maxdepth || depth+get_h()>maxdepth) return;  //可行性剪枝
    if(get_h()==0)  //中心相同了
    {
        flag=true;
        finop[depth]='\0';
        printf("%s\n%d\n",finop,mp[center[0]]);
        return;
    }
    for(int nextop=0;nextop<8;nextop++)  //从A开始搜索
    {
        if(nextop!=reverseop[lastop])  //与上一次操作不互逆
        {
            option(nextop);
            finop[depth]=nextop+'A';
            dfs(depth+1,nextop,maxdepth);
            option(reverseop[nextop]);  //回溯还原
        }
    }
}

int main()
{
    while(1)
    {
        for(int i=0;i<24;i++)
        {
            scanf("%d",&mp[i]);
            if(mp[i]==0) return 0;
        }
        if(get_h()==0)
        {
            printf("No moves needed\n%d\n", mp[center[0]]);
            continue;
        }
        flag=false;
        for(int depth=1;!flag;depth++) //迭代加深
        {
            dfs(0,8,depth);
        }
    }
    return 0;
}