JZOJ5466. 【NOIP2017提高A组冲刺11.9】玩游戏

Description

小A得了忧郁综合症，小B正在想办法开导她。
机智的小B决定陪着小A玩游戏，他从魔法的世界里变出一张无向联通图，每条边上都有边权。小B定义一条路径的权值为所有经过边中的最大权值，小A则定义两点的最短路径为所有路径中权值最小的路径权。
每次小A和小B会选出k对点mi_1,mi_2，分别计算出mi_1,mi_2的最短路径ti,然后小B会拿出k堆灵魂宝石，每堆有ti个。然后小A先从一堆中选出若干个灵魂宝石拿走，接下来小B重复同样的操作，如此反复，直到取走最后一颗灵魂宝石，然后取走最后一颗宝石的人获胜。
小B认为这样游戏太简单，于是他会不定期向这张图上加上一些边，以增大游戏难度。
小A具有预知未来的能力，她看到了自己和小B在未来游戏中的选择，以及小B增加的边。现在对于每次游戏，小A想知道自己是否存在必胜的方法。但是预知未来已经消耗了她太多精力，出于疲惫她只好找到了你。

Input

第一行三个数N和M和K，表示这张无向图初始的点数与边数，以及每次询问的点对的个数；
接下来M行，每行三个数u,v,q，表示点u和点v之间存在一条权值为q的
边；
接下来一行一个数Q，表示操作总数；
接下来Q行，表示操作，每行格式为下面两条中的一条：
1.add u v q：表示在u与v之间加上一条边权为q的边；
2.game m1_1 m1_2 … mk_1 mk_2：表示一次游戏中选择的k对点。
数据保证1≤u,v,mi_1,mi_2≤n，1≤q，mi_1≠mi_2

Output

对于每个game输出一行，若小A存在必胜策略，则输出“madoka”，否则输出“Baozika”，以回车结尾

Sample Input

5 6 2
1 2 3
2 3 6
4 2 4
5 3 5
3 4 5
5 1 5
4
game 1 3 4 3
game 1 5 2 4
add 2 5 4
game 1 5 3 4

Sample Output

Baozika
madoka
madoka

数据范围

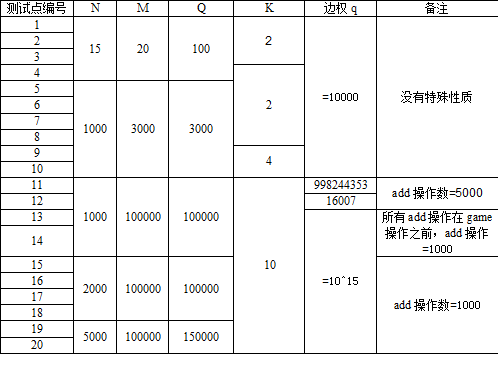
首先，先要有一个结论，
如果宝石异或和为0，则先手输，否则就先手赢。

简单说一下吧，
如果不为0，则先手闭有一种方法使得它变为0，
当异或和为0的时候，无论怎样都会改变。
最后的异或和一定是0的。

因为求最大边权的最小值，
很显然是最小生成树。

加边操作只有1000次，
每次暴力重构都没有问题，
而询问就用倍增lca解决。

code

#include
#include
#include
#include
#include
#define ll long long
#define N 5050
using namespace std;

char ch;
void read(int& n)
{
    n=0;
    for(ch=getchar();ch<'0' || ch>'9';ch=getchar());
    for(;'0'<=ch && ch<='9';n=(n<<3)+(n<<1)+ch-48,ch=getchar());
}
void readl(ll& n)
{
    n=0;
    for(ch=getchar();ch<'0' || ch>'9';ch=getchar());
    for(;'0'<=ch && ch<='9';n=(n<<3)+(n<<1)+ch-48,ch=getchar());
}

struct node
{
    int x,y;ll z;
}a[N],c[N*20];

bool cmp(node a,node b)
{
    return a.zint n,m,k,q,x,y,nxt[N*40],b[N],to[N*40],tot;
ll z,v[N*40],sum,g[N][13];
int fa[N],f[N][13],deep[N],t,f1,f2,useless;
bool bz[2*N],vis[N];

ll min(ll x,ll y){return x<y?x:y;}
ll max(ll x,ll y){return x>y?x:y;}

void ins(int x,int y,ll z)
{
    nxt[++tot]=b[x];
    to[tot]=y;
    v[tot]=z;
    b[x]=tot;
}

ll lca(int x,int y)
{
    ll mx=0;
    if(deep[y]>deep[x])swap(x,y);
    for(int i=12;i>=0;i--)
        if(deep[f[x][i]]>=deep[y])mx=mxx][i]?g[x][i]:mx,x=f[x][i];

    if(x==y)return mx;

    for(int i=12;i>=0;i--)
        if(f[x][i]!=f[y][i])mx=mxx][i]?g[x][i]:mx,x=f[x][i],mx=mxy][i]?g[y][i]:mx,y=f[y][i];

    mx=mxx][0]?g[x][0]:mx,mx=mxy][0]?g[y][0]:mx;
    return mx;
}

void dfs(int x)
{
    vis[x]=0;
    //printf("%d\n",deep[x]);
    for(int i=b[x];i;i=nxt[i])
        if(vis[to[i]])
        {
            f[to[i]][0]=x;
            deep[to[i]]=deep[x]+1;
            g[to[i]][0]=v[i];
            dfs(to[i]);
        }
}

int get(int x)
{
    if(fa[x]!=x)fa[x]=get(fa[x]);
    return fa[x];
}

void reset()
{
    tot=t=0;sort(a+1,a+n+1,cmp);
    memset(b,0,sizeof(b));
    memset(vis,1,sizeof(vis));
    for(int i=1;i<=n;i++)
        fa[i]=i;
    for(int i=1;i<=n;i++)
    {
        f1=get(a[i].x);
        f2=get(a[i].y);
        if(f1!=f2)
        {
            ins(a[i].x,a[i].y,a[i].z);
            ins(a[i].y,a[i].x,a[i].z);
            fa[f2]=f1;
            t++;
        }else useless=i;
    }
    deep[1]=1;
    dfs(1);
    for(int j=1;j<13;j++)
        for(int i=1;i<=n;i++)
            f[i][j]=f[f[i][j-1]][j-1],g[i][j]=max(g[i][j-1],g[f[i][j-1]][j-1]);
} 

void pre()
{
    sort(c+1,c+1+m,cmp);
    for(int i=1;i<=n;i++)
        fa[i]=i;
    for(int i=1;t1;i++)
    {
        f1=get(c[i].x);
        f2=get(c[i].y);
        if(f1!=f2)
        {
            fa[f2]=f1;
            t++;
            a[t]=c[i];
        }
    }
    a[n]=c[m];
}

int main()
{
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    read(n);read(m);read(k);
    for(int i=1;i<=m;i++)
        read(c[i].x),read(c[i].y),readl(c[i].z);

    pre();
    reset();

    read(q);
    for(int i=1;i<=q;i++)
    {
        for(ch=getchar();ch!='g' && ch!='a';ch=getchar());
        if(ch=='g')
        {
            sum=0;
            for(int j=1;j<=k;j++)
                read(x),read(y),sum=sum^lca(x,y);
            if(sum)printf("madoka\n");else printf("Baozika\n");
        }
        else read(a[useless].x),read(a[useless].y),readl(a[useless].z),reset();
    }

    return 0;
}