选择排序
前言
原理:每次循环对比找出最小/大值,将最值的元素交换至左侧
思想:直接选择排序(Straight Select Sort)算法思想:第一趟从n个元素的数据序列中选出关键字最小/大的元素并放在最前/后位置,下一趟从n-1个元素中选出最小/大的元素并放在最前/后位置。以此类推,经过n-1趟完成排序
案例分析:
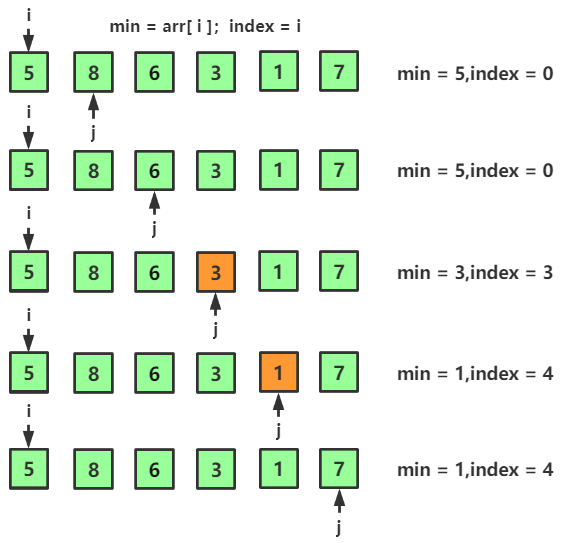
1、初始的无序数列 {5,8,6,3,1,7},希望对其升序排序
内层循环经过一轮对比后找到最小值,min = 1,下标为 index = 4;交换位置
代码实现
第 1 版代码
public static void straightSelectSort(int[] arr){
//i不需要 = 数组最尾部元素,因为后面没有值对比了
for (int i = 0; i < arr.length - 1; i++) {
//设置每次循环的起始点为最小/大值
int min = arr[i];
//记录下最小/大值的下标
int index = i;
for (int j = i + 1; j < arr.length; j++) {
//升序排序>,降序排序<
if (min > arr[j]){
min = arr[j];
index = j;
}
}
//一轮对比完成后,将默认的最小值赋予到找到的最值下标位置
arr[index] = arr[i];
//把找到的真实最值放到前面
arr[i] = min;
}
}
这里其实有可能出现默认的最小值其实就是真正的最小值,所以一轮内层循环下来,是没有交换数据,可以添加哨兵,如果没有找到最小值,就不进行值的交换,减少交换次数。
第 2 版代码
public static void straightSelectSort(int[] arr){
//i不需要 = 数组最尾部元素,因为后面没有值对比了
for (int i = 0; i < arr.length - 1; i++) {
//设置每次循环的起始点为最小/大值
int min = arr[i];
//记录下最小/大值的下标
int index = i;
//哨兵,记录是否找到最值,默认false
boolean isSwap = false;
for (int j = i + 1; j < arr.length; j++) {
//升序排序>,降序排序<
if (min > arr[j]){
min = arr[j];
index = j;
//找到最值,设置为true
isSwap = true;
}
}
if (isSwap){
//一轮对比完成后,将默认的最小值赋予到找到的最值下标位置
arr[index] = arr[i];
//把找到的真实最值放到前面
arr[i] = min;
}
}
}
直接选择排序算法复杂度分析:
如果数组中有**n个元素
第1轮循环是arr[0] 和arr[1] ...arr[n-1] 进行比较,次数为n-1 次,arr[0]放最值。
第2轮循环是arr[1] 和 arr[2]...arr[n-1] 进行比较,次数为n-2次,arr[1]放第二个最值。
所以不难得出它的比较的次数是n-1 + n-2 + n-3 + ....1 = n*(n-1)/2 。
时间复杂度为 = n^2/2- n/2 = n^2 ,O(n^2)。
算法升级
分析
直接选择排序每一次查找只是找出最小值,可以这么改进,查找最小值的同时,找到一个最大值,然后将两者分别放在它们应该出现的位置,这样遍历的次数就会减少,同时添加哨兵,如果没有找到最值,不发生交换
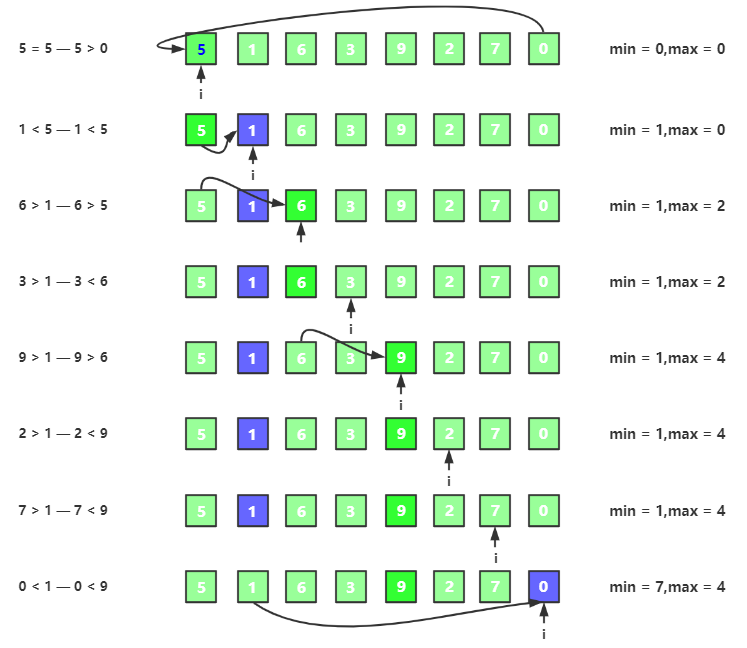
以新的无序数列 {5,1,6,3,9,2,7,0}为例,按照上面的分析,初始状态如下:
排序过程如下:
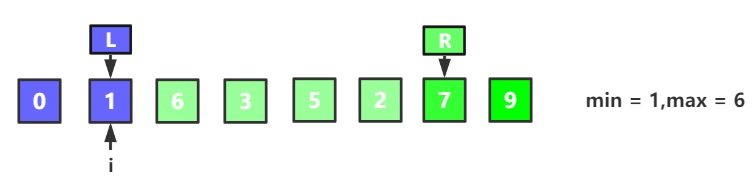
交换最值,将最小值放到arr[left],最大值放到arr[right],同时left++,right--;准备下一轮循环,第一轮结果如下:
算法注意点:
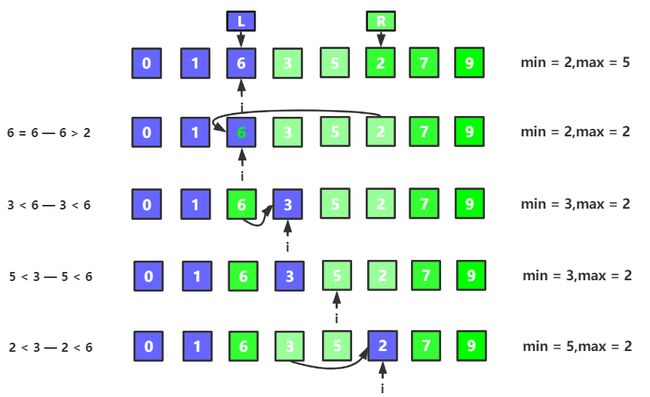
(1) 第二轮开始对比前,我们可以发现,此时arr[left]与arr[right]恰好是此轮的最值,因此应该加上哨兵,对此情况,内循环走完后,不进行值交换,判断条件:min == right && max == left
(2) 特别注意的地方:第三轮循环后,可以发现的点是,left = 2,right = 5,而结果是min = 5,max = 2,仔细看你就发现了,left与min对应,而max与right对应,结果是值反面的的,所以在进行值交换的时候,进行一次就可以了,否则交换两次,就变成了巴黎铁塔翻过来又翻回去了,判断条件:min == right && max == left
进化版代码
public static void betterSelectSort(int[] arr) {
//left指针指向无序边界起点,right指针指向终点,temp用作临时变量交换值
int left,right,temp;
//默认指向无序列表起点
left = 0;
//默认指向无序列表终点
right = arr.length - 1;
//记录每轮找到的最小值的下标
int min = left;
//记录每轮找到的最大值的下标
int max = right;
//当right >= left时,列表已经有序
//记录循环的次数
int index = 0;
while(left < right) {
min = left; //每轮开始前,默认无序列表起点为最小值
max = right; //每轮开始前,默认无序列表终点为最大值
//指针i从左往右扫描,找出最小值,最大值
for (int i=left; i<=right; i++) {
if (arr[i]arr[max]) {
max = i; //通过比较,记录最大值的下标
}
}
index++;
if (min == left && max == right){
System.out.println("第" + index + "轮循环没有找到最值,无需交换");
}else if (min == right && max == left){
//交换一次即可,交换两次的话,序列翻转,相当于没有交换
temp = arr[left];
arr[left] = arr[min];
arr[min] = temp;
}else {
//找到最小值,交换
temp = arr[left];
arr[left] = arr[min];
arr[min] = temp;
//找到最大值,交换
temp = arr[right];
arr[right] = arr[max];
arr[max] = temp;
}
//确定最小/大值,指针向中间移动
left++;right--;
}
}
优化后代码虽然有效的减少了外层循环的次数,但其时间复杂度仍然是O(n^2)
文章为原创,转载请声明出处
更多文章,欢迎点赞关注,我的掘金:https://juejin.im/user/1151943919304840/posts