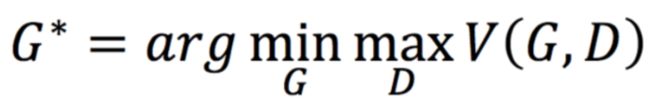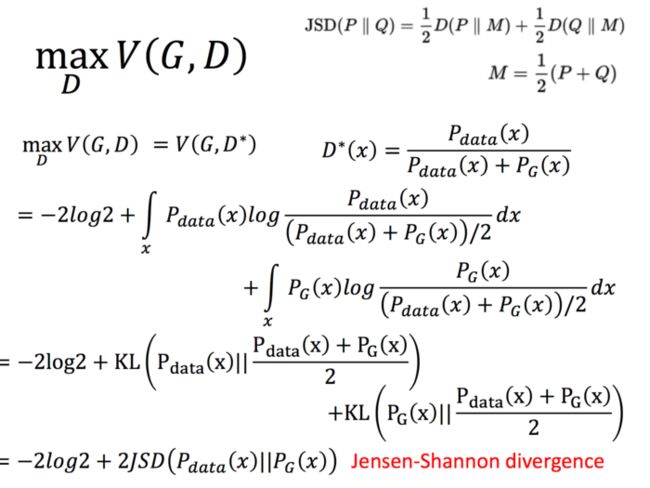GAN(生成对抗网络)简介
最近看了李宏毅老师的深度学习视频课程,真的是讲得十分细致,从头到尾看下来一遍,对深度学习模型有了一个基本的认识,趁着脑子还能记着一些东西,赶紧把学到的东西记录下来,以备后用。
视频地址:https://www.bilibili.com/video/av9770302/from=search&seid=905421046757750252
ppt地址:http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html
1、什么是GAN
GAN 主要包括了两个部分,即生成器 generator 与判别器 discriminator。生成器主要用来学习真实图像分布从而让自身生成的图像更加真实,以骗过判别器。判别器则需要对接收的图片进行真假判别。在整个过程中,生成器努力地让生成的图像更加真实,而判别器则努力地去识别出图像的真假,这个过程相当于一个二人博弈,随着时间的推移,生成器和判别器在不断地进行对抗,最终两个网络达到了一个动态均衡:生成器生成的图像接近于真实图像分布,而判别器识别不出真假图像,对于给定图像的预测为真的概率基本接近 0.5(相当于随机猜测类别)。
对于 GAN 更加直观的理解可以用一个例子来说明:造假币的团伙相当于生成器,他们想通过伪造金钱来骗过银行,使得假币能够正常交易,而银行相当于判别器,需要判断进来的钱是真钱还是假币。因此假币团伙的目的是要造出银行识别不出的假币而骗过银行,银行则是要想办法准确地识别出假币。
因此,我们可以将上面的内容进行一个总结。给定真 = 1,假 = 0,那么有:
对于给定的真实图片(real image),判别器要为其打上标签 1;
对于给定的生成图片(fake image),判别器要为其打上标签 0;
对于生成器传给辨别器的生成图片,生成器希望辨别器打上标签 1。
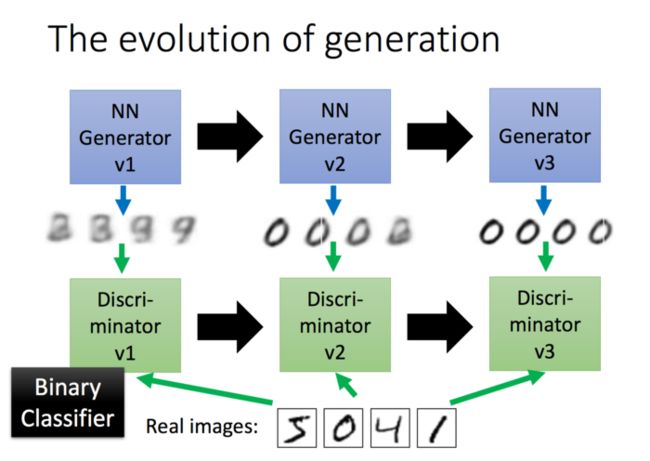
好了,上面大家应该已经对GAN有了一个基本的认识,那么GAN是如何来做的呢?首先,我们又一个第一代的Generator,然后他产生一些图片,然后我们把这些图片和一些真实的图片丢到第一代的Discriminator里面去学习,让第一代的Discriminator能够真实的分辨生成的图片和真实的图片,然后我们又有了第二代的Generator,第二代的Generator产生的图片,能够骗过第一代的Discriminator,此时,我们在训练第二代的Discriminator,依次类推。
image.png
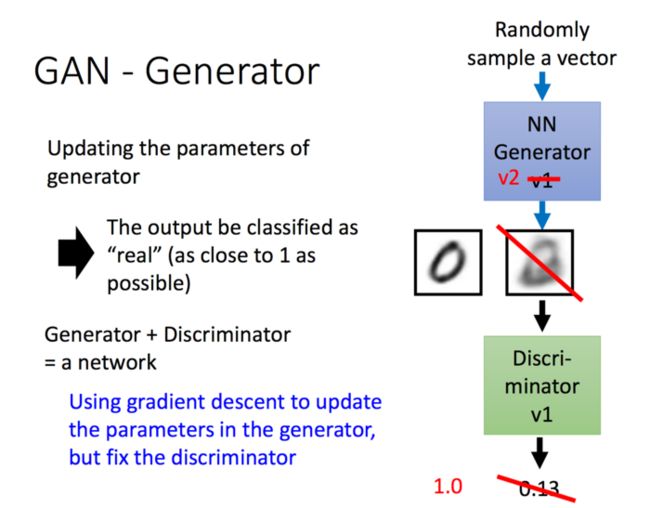
刚才的描述中,你可能不太明白如何训练新一代的Generator来骗过上一代的Discriminator,方法其实很简单,你可以把新一代的Generator和上一代的Discriminator连起来形成一个新的NN,我们希望最终的输出接近1,然后我们就可以拿中间的结果当作我们的新的图片的输出,下图很形象的显示了上面的过程:
2、GAN原理深入
先来回顾一下我们的极大似然估计,假设我们有一大堆data,他的分布是Pdata(x),我们可以认为这里的data就是一大堆图片,但是,我们有了这一大堆东西,再想生成一个新的data是不容易的,因为我们不知道这个分布的具体参数,所以,我们就想估计这堆数据的所服从的参数。那么,我们可以从Pdata(x)产生一大堆sample,然后,我们就希望找一组参数,使得服从这组参数的分布产生这堆sample的可能性最大。
下面是极大似然估计的化简过程,因为这堆sample都是从Pdata(x)里面出来的,所以,我们可以进行下面的约等转换。然后我们把期望转换为积分,同时加上后面一项(后面一项是一个常数,只是为了更简单的表示KL散度)
KL散度又称相对熵。设P(x)和Q(x)是X取值的两个概率概率分布,则对的相对熵为:
在一定程度上,熵可以度量两个随机变量的距离。KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下,P表示数据的真实分布,Q表示数据的理论分布,模型分布,或P的近似分布。
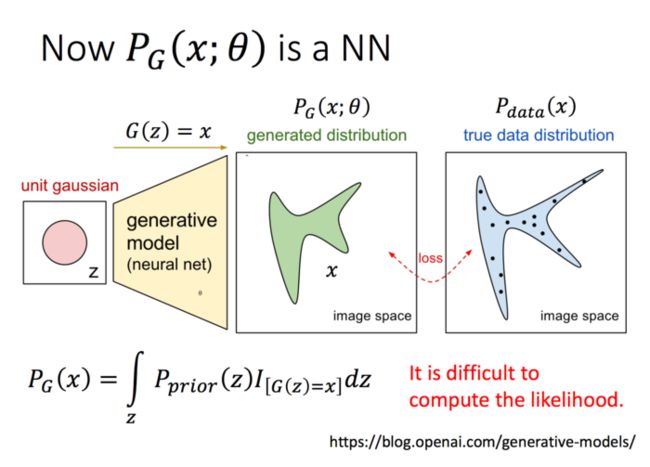
那么,在GAN中,我们用NN的参数表示PG的参数θ:
那么 ,GAN的基本原理如下:
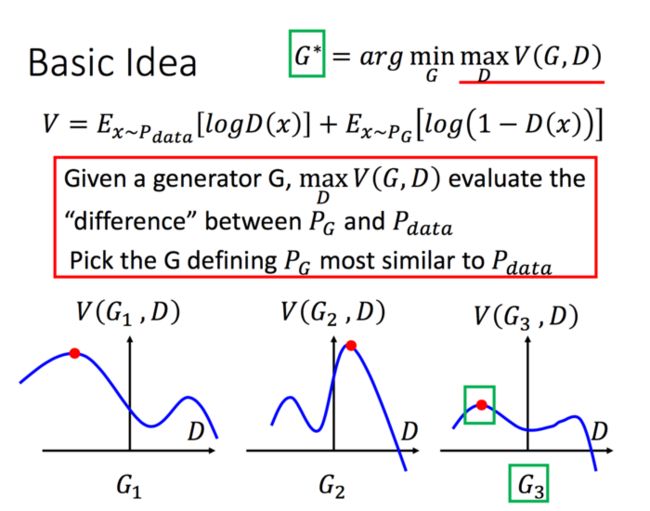
所以,我们最终的求解目标是:
我们可以用下面的图来形象的表示上面的求解问题,看下面的图,我们可以很清楚的知道,我们要找的G就是G3,而D则是最高点的D。
那么 ,V是什么,V写作下面的式子,你不必管这个东西怎么来的,我只想说,能想到这个的人真的是太可怕了。当我们的V写成下面这样子的时候,我们取maxV(G,D)就饿能表示Pg和Pdata的差异。
image.png
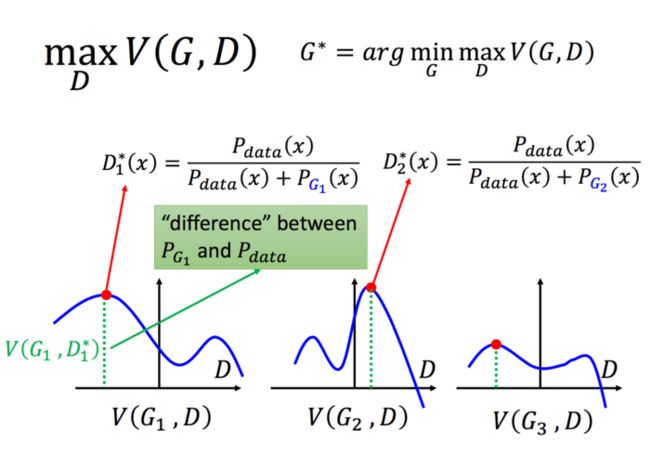
为什么V要写成这样能表示二者的差异呢?这个可以通过严格的数学证明推导出,这里,对于一个给定的G,我们来求解maxV(G,D):
对于任何一个常数,因为Pdata和G这里都是给定的,我们可以认为这里是常数,那么D取什么可以得到最大呢,很简单,导数为0的情况下。
在有了D的值之后,我们就可以带入原式中啦:
继续化简,我们可以得到两个KL散度,进而得到JS散度:
相信大家对于求解得到D的过程已经非常明白了,我自己再推到一下后面的式子吧,希望能够比PPT更加明白一些:
所以,现在我们就明白了,按照上面的V的定义,我们就能得到二者的差距,当然我们可以定别的,就能产生别的散度度量。
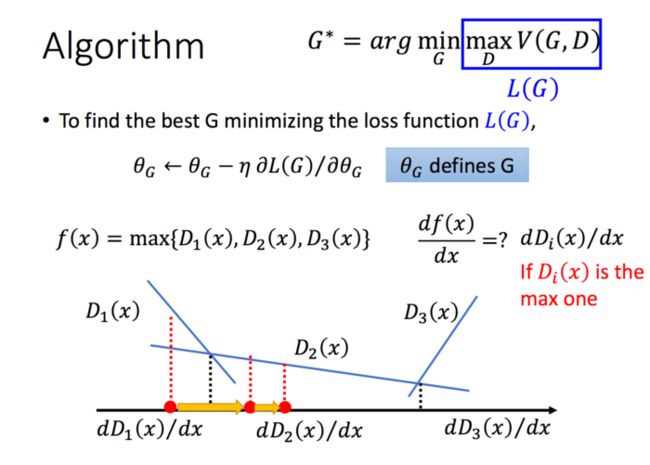
那么,给定了一个G,我们能够通过最大化V得到D,那么我们如何求解G呢,用梯度下降就好啦:
3、实际中的GAN
刚才我们讲的是理论部分的内容,但是在实际中,Pdata和Pg我们是不知道的,我们没办法穷举所有的x,所以,我们只能采用采样的方法,同时可以采用我们二分类的思路,我们把Pdata(x)中产生的样本当作正例,把Pg(x)产生的样本当作负例,那么,下面V可以看作是我们二分类的一个损失函数的相反数(少了负号嘛):
也就是说,最大化V的话,其实就是最小化我们二分类的损失,下面的Minimize少了一个负号,所以我们要找的D,就是能使二分类的损失最小的D,也就是能够正确分辨Pdata和Pg(x)的D,这也正符合我们想要找的discriminator的定义,是不是很神奇!
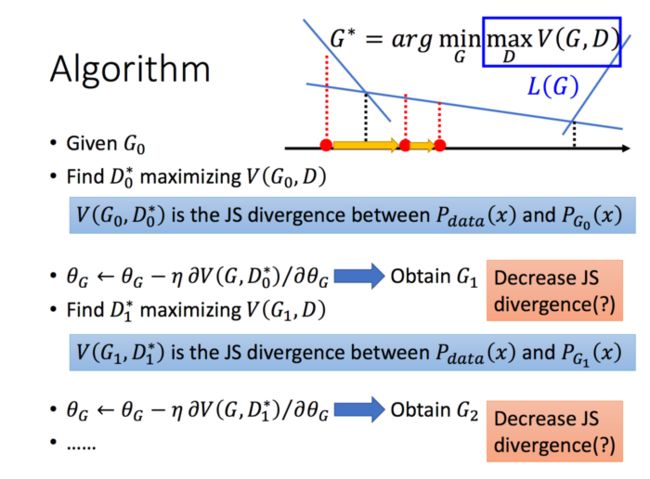
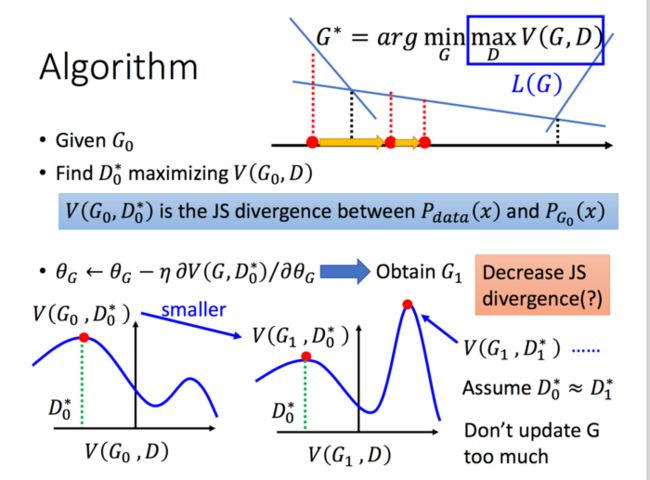
所以,总结一下,实践中我们的GAN基于如下的步骤:
上面的步骤很好的解释了我们刚才对于GAN的解释:首先,我们又一个第一代的Generator,然后他产生一些图片,然后我们把这些图片和一些真实的图片丢到第一代的Discriminator里面去学习,让第一代的Discriminator能够真实的分辨生成的图片和真实的图片,然后我们又有了第二代的Generator,第二代的Generator产生的图片,能够骗过第一代的Discriminator,此时,我们在训练第二代的Discriminator,依次类推。
在实际中,我们有可能做下面的变换,可以加快我们的训练速度: