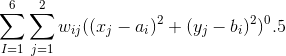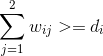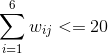matlab学习——选址问题（线性规划和非线性规划规划）

线性规划

某公司有6个建筑工地，位置坐标为(ai,bi) (单位：公里),水泥日用量di (单位：吨）

i	１	２	３	４	５	６
a	1.25	8.75	0.5	5.75	3	7.25
b	1.25	0.75	4.75	5	6.5	7.75
d	3	5	4	7	6	11

v假设：料场和工地之间有直线道路

（1）现有2料场，位于A(5,1),B(2,7),记(xj,yj),j=1,2, 日储量qj各有20吨。

目标：制定每天的供应计划，即从A, B两料场分别向各工地运送多少吨水泥，使总的吨公里数最小。

分析：

我们知道我们要求的是水泥吨数，现在我们用来代表第j个料场向第i个工地送料的吨数

我们要求的目标函数

为minZ=

约束条件有两个

1 向每个料场运输的量要不小于日用量

2 每个料场向外运输的量不能大于自身所有的储备量

 且wij要大于等于零。

这个约束形式很简单，但是难点在于如何将wij这个二维未知数，变成一维 未知数

clc,clear
%先来将函数系数构造出来
a=[1.25,8.75,0.5,5.75,3,7.25]; 
b=[1.25,0.75,4.75,5,6.5,7.75]; 
d=[3,5,4,7,6,11]; e=[20,20]; 
x=[5,2];y=[1,7]; 
for i=1:6
    for j=1:2
        s(i,j)=((x(j)-a(i))^2+(y(j)-b(i))^2)^(1/2);
    end
end
f=s(:);
%拉伸处理之后，wij的系数被重新洗牌，比如w11就是f(1)，w12就是f(7)
%下面构造约束条件涉及的矩阵为
A=[1 1 1 1 1 1 0 0 0 0 0 0; 0 0 0 0 0 0 1 1 1 1 1 1];
b=e;
Aeq=[1 0 0 0 0 0 1 0 0 0 0 0
   0 1 0 0 0 0 0 1 0 0 0 0
   0 0 1 0 0 0 0 0 1 0 0 0 
   0 0 0 1 0 0 0 0 0 1 0 0
   0 0 0 0 1 0 0 0 0 0 1 0
   0 0 0 0 0 1 0 0 0 0 0 1];
beq=d;
lb=zeros(1,12);
[x,fval]=linprog(f,A,b,Aeq,beq,lb)

非线性规划

（2）改建两个新料场，需要确定新料场位置(xj,yj)和运量cij ，在其它条件不变下使总吨公里数最小。 

此时的决策变量从12个变成了16个，分别是吨数和选址坐标

minZ=

可以利用lingo来解

model:
title mubiao;
sets:
supply/1,2/:e,x,y;
demand/1..6/:d,a,b;
link(demand,supply):c;
endsets
data:
e=20,20;
a=1.25,8.75,0.5,5.75,3,7.25;
b=1.25,0.75,4.75,5,6.5,7.75;
d=3,5,4,7,6,11;
enddata
!非线性规划，要有初始值;
init:
x,y=5,2,1,7;!实际赋值顺序是x=(5,1),y=(2,7),可以看出lingo是按照列赋值的;
endinit
[obj]min=@sum(link(i,j):c(i,j)*((x(j)-a(i))^2+(y(j)-b(i))^2)^(1/2));
@for(demand(i):@sum(supply(j):c(i,j))=d(i));
@for(supply(j):@sum(demand(i):c(i,j))<=e(j));
@for(supply(j):@bnd(0.5,x,8.75);@bnd(0.75,x,7.75));