Python数值计算工具 ——Numpy（调用常用的数学和统计函数）

0、前言

python基础语法中有讲解有关存储数据的列表对象，但是其无法直接参与数值运算（虽然可以使用加法和乘法，但分别代表列表元素的增加和重复）。
本文将介绍另一种非常有用的数据结构，那就是数组，通过数组可以实现各种常见的数学运算，而且基于数组的运算，也是非常高效的。 本章的重点是讲解有关Python数值运算的numpy模块，通过numpy模块的学习，你将掌握如下几方面的内容，进而为后面的统计运算和机器学习打下基础：

• 数组的创建与操作；
• 数组的基本数学运算；
• 常用数学和统计函数；
• 线性代数的求解；
• 伪随机数的创建。

1、数组的创建与操作

通过numpy模块中的array函数实现数组的创建，如果向函数中传入一个列表或元组，将构造简单的一维数组；如果传入多个嵌套的列表或元组，则可以构造一个二维数组。构成数组的元素都是同质的，即数组中的每一个值都具有相同的数据类型，下面分别构造一个一维数组和二维数组。

1.1 数组的创建

# 导入模块，并重命名为np
import numpy as np
# 单个列表创建一维数组
arr1 = np.array([3,10,8,7,34,11,28,72])
# 嵌套元组创建二维数组
arr2 = np.array(((8.5,6,4.1,2,0.7),(1.5,3,5.4,7.3,9),(3.2,3,3.8,3,3),(11.2,13.4,15.6,17.8,19)))
print('一维数组：\n',arr1)
print('二维数组：\n',arr2)

结果：

一维数组：
 [ 3 10  8  7 34 11 28 72]
二维数组：
 [[ 8.5  6.   4.1  2.   0.7]
 [ 1.5  3.   5.4  7.3  9. ]
 [ 3.2  3.   3.8  3.   3. ]
 [11.2 13.4 15.6 17.8 19. ]]

如上结果所示，可以将列表或元组转换为一个数组，在第二个数组中，输入的元素含有整数型和浮点型两种数据类型，但输出的数组元素全都是浮点型（原来的整型会被强制转换为浮点型，从而保证数组元素的同质性）。
使用位置索引可以实现数组元素的获取，虽然在列表中讲解过如何通过正向单索引、负向单索引、切片索引和无限索引获取元素，但都无法完成不规律元素的获取，如果把列表转换为数组，这个问题就可以解决了，下面介绍具体的操作。

1.2 数组元素的获取

先来看一下一维数组元素与二维数组元素获取的例子，代码如下：

# 一维数组元素的获取
print(arr1[[2,3,5,7]])

# 二维数组元素的获取
# 第2行第3列元素
print(arr2[1,2])
# 第3行所有元素
print(arr2[2,:])
# 第2列所有元素
print(arr2[:,1])
# 第2至4行，2至5行
print(arr2[1:4,1:5])

结果：

[ 8  7 11 72]
5.4
[3.2 3.  3.8 3.  3. ]
[ 6.   3.   3.  13.4]
[[ 3.   5.4  7.3  9. ]
 [ 3.   3.8  3.   3. ]
 [13.4 15.6 17.8 19. ]]

如上结果是通过位置索引获取一维和二维数组中的元素，在一维数组中，列表的所有索引方法都可以使用在数组上，而且还可以将任意位置的索引组装为列表，用作对应元素的获取；在二维数组中，位置索引必须写成[rows,cols]的形式，方括号的前半部分用于控制二维数组的行索引，后半部分用于控制数组的列索引。如果需要获取所有的行或列元素，那么，对应的行索引或列索引需要用英文状态的冒号表示。但是，要是从数组中取出某几行和某几列，通过[rows,cols]的索引方法就不太有效了，例如：

# 第一行、最后一行和第二列、第四列构成的数组
print(arr2[[0,-1],[1,3]])
# 第一行、最后一行和第一列、第三列、第四列构成的数组
print(arr2[[0,-1],[1,2,3]])

结果：

[ 6.  17.8]
---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-3-05bfd30b63fe> in <module>
      2 print(arr2[[0,-1],[1,3]])
      3 # 第一行、最后一行和第一列、第三列、第四列构成的数组
----> 4 print(arr2[[0,-1],[1,2,3]])

IndexError: shape mismatch: indexing arrays could not be broadcast together with shapes (2,) (3,) 

如上结果所示，第一个打印结果并不是2×2的数组，而是含两个元素的一维数组，这是因为numpy将[[0,-1],[1,3]]组合的理解为了[0,1]和[-1,3]；同样，在第二个元素索引中，numpy仍然将[[0,-1],[1,2,3]]组合理解为拆分单独的[rows,cols]形式，最终导致结果中的错误信息。实际上，numpy的理解是错误的，第二个输出应该是一个2×3的数组。为了克服[rows,cols]索引方法的弊端，建议读者使用ix_函数，具体操作如下：

# 第一行、最后一行和第二列、第四列构成的数组
print(arr2[np.ix_([0,-1],[1,3])])
# 第一行、最后一行和第一列、第三列、第四列构成的数组
print(arr2[np.ix_([0,-1],[1,2,3])])

结果：

[[ 6.   2. ]
 [13.4 17.8]]
 
[[ 6.   4.1  2. ]
 [13.4 15.6 17.8]]

1.3 数组的常用属性

如果不是手工写入的数组，而是从外部读入的数据，此时也许对数据就是一无所知，如该数据的维数、行列数、数据类型等信息，下面通过简短的代码来了解数组的几个常用属性，进而跨出了解数据的第一步。
在numpy模块中，可以通过genfromtxt函数读取外部文本文件的数据，这里的文本文件主要为csv文件和txt文件。关于该函数的语法和重要参数含义如下：

np.genfromtxt(fname, dtype=<class ‘float’>, comments="#", delimiter=None, skip_header=0,
			  skip_footer=0, converters=None, missing_values=None, filling_values=None, usecols=None,
			  names=None,)

• fname：指定需要读入数据的文件路径。
• dtype：指定读入数据的数据类型，默认为浮点型，如果原数据集中含有字符型数据，必须指定数据类型为“str”。
• comments：指定注释符，默认为“#”，如果原数据的行首有“#”,将忽略这些行的读入。
• delimiter：指定数据集的列分割符。
• skip_header：是否跳过数据集的首行，默认不跳过。
• skip_footer：是否跳过数据集的脚注，默认不跳过。
• converters：将指定列的数据转换成其他数值。
• miss_values：指定缺失值的标记，如果原数据集含指定的标记，读入后这样的数据就为缺失值。
• filling_values：指定缺失值的填充值。
• usecols：指定需要读入哪些列。
• names：为读入数据的列设置列名称。

接下来通过上面介绍的数据读入函数，读取学生成绩表数据，然后使用数组的几个属性，进一步掌握数据的结构情况。

# 读入数据
stu_score = np.genfromtxt(fname = r'C:\Users\Administrator\Desktop\stu_socre.txt',delimiter='\t',skip_header=1)
# 查看数据结构
print(type(stu_score))
# 查看数据维数
print(stu_score.ndim)
# 查看数据行列数
print(stu_score.shape)
# 查看数组元素的数据类型
print(stu_score.dtype)
# 查看数组元素个数
print(stu_score.size)

结果：

<class 'numpy.ndarray'>
2
(1380, 5)
float64
6900

如上结果所示，读入的学生成绩表是一个二维的数组（type函数和ndim方法），一共包含1380行观测和5个变量（shape方法），形成6900个元素（size方法），并且这些元素都属于浮点型（dtype方法）。通过上面的几个数组属性，就可以大致了解数组的规模。

1.4 数组的形状处理

数组形状处理的手段主要有reshape、resize、ravel、flatten、vstack、hstack、row_stack和colum_stack，下面通过简单的案例来解释这些“方法”或函数的区别。

arr3 = np.array([[1,5,7],[3,6,1],[2,4,8],[5,8,9],[1,5,9],[8,5,2]])
# 数组的行列数
print(arr3.shape)
# 使用reshape方法更改数组的形状
print(arr3.reshape(2,9))
# 打印数组arr3的行列数
print(arr3.shape)

# 使用resize方法更改数组的形状
print(arr3.resize(2,9))
# 打印数组arr3的行列数
print(arr3.shape)

结果：

(6, 3)
[[1 5 7 3 6 1 2 4 8]
 [5 8 9 1 5 9 8 5 2]]
(6, 3)
None
(2, 9)

如上结果所示，虽然reshape和resize都是用来改变数组形状的“方法”，但是reshape方法只是返回改变形状后的预览，但并未真正改变数组arr3的形状；而resize方法则不会返回预览，而是会直接改变数组arr3的形状，从前后两次打印的arr3形状就可以发现两者的区别。如果需要将多维数组降为一维数组，利用ravel、flatten和reshape三种方法均可以轻松解决：

arr4 = np.array([[1,10,100],[2,20,200],[3,30,300]])
print('原数组：\n',arr4)
# 默认排序降维
print('数组降维：\n',arr4.ravel())
print(arr4.flatten())
print(arr4.reshape(-1))
# 改变排序模式的降维
print(arr4.ravel(order = 'F'))
print(arr4.flatten(order = 'F'))
print(arr4.reshape(-1, order = 'F'))

结果：

原数组：
 [[  1  10 100]
 [  2  20 200]
 [  3  30 300]]
数组降维：
 [  1  10 100   2  20 200   3  30 300]
[  1  10 100   2  20 200   3  30 300]
[  1  10 100   2  20 200   3  30 300]
[  1   2   3  10  20  30 100 200 300]
[  1   2   3  10  20  30 100 200 300]
[  1   2   3  10  20  30 100 200 300]

如上结果所示，在默认情况下，优先按照数组的行顺序，逐个将元素降至一维（见数组降维的前三行打印结果）；如果按原始数组的列顺序，将数组降为一维的话，需要设置order参数为“F”（见数组降维的后三行打印结果）。尽管这三者的功能一致，但之间是否存在差异呢？接下来对降维后的数组进行元素修改，看是否会影响到原数组arr4的变化：

# 更改预览值
arr4.flatten()[0] = 2000
print('flatten方法：\n',arr4)
arr4.ravel()[1] = 1000
print('ravel方法：\n',arr4)
arr4.reshape(-1)[2] = 3000
print('reshape方法：\n',arr4)

结果：

flatten方法：
 [[  1  10 100]
 [  2  20 200]
 [  3  30 300]]
ravel方法：
 [[   1 1000  100]
 [   2   20  200]
 [   3   30  300]]
reshape方法：
 [[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]]

如上结果所示，通过flatten方法实现的降维返回的是复制，因为对降维后的元素做修改，并没有影响到原数组arr4的结果；相反，ravel方法与reshape方法返回的则是视图，通过对视图的改变，是会影响到原数组arr4的。
vstack用于垂直方向（纵向）的数组堆叠，其功能与row_stack函数一致，而hstack则用于水平方向（横向）的数组合并，其功能与colum_stack函数一致，下面通过具体的例子对这四种函数的用法和差异加以说明。

arr5 = np.array([1,2,3])
print('vstack纵向合并数组：\n',np.vstack([arr4,arr5]))
print('row_stack纵向合并数组：\n',np.row_stack([arr4,arr5]))

结果：

vstack纵向合并数组：
 [[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]
 [   1    2    3]]
row_stack纵向合并数组：
 [[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]
 [   1    2    3]]

arr6 = np.array([[5],[15],[25]])
print('hstack横向合并数组：\n',np.hstack([arr4,arr6]))
print('column_stack横向合并数组：\n',np.column_stack([arr4,arr6]))

结果：

hstack横向合并数组：
 [[   1 1000 3000    5]
 [   2   20  200   15]
 [   3   30  300   25]]
column_stack横向合并数组：
 [[   1 1000 3000    5]
 [   2   20  200   15]
 [   3   30  300   25]]

print(arr4)
print('垂直方向计算数组的和：\n',np.sum(arr4,axis = 0))
print('水平方向计算数组的和：\n',np.sum(arr4, axis = 1))

结果：

[[   1 1000 3000]
 [   2   20  200]
 [   3   30  300]]
垂直方向计算数组的和：
 [   6 1050 3500]
水平方向计算数组的和：
 [4001  222  333]

如上结果所示，前两个输出是纵向堆叠的效果，后两个则是横向合并的效果。如果是多个数组的纵向堆叠，必须保证每个数组的列数相同；如果将多个数组按横向合并的话，则必须保证每个数组的行数相同。

2、数组的基本运算符

本文开头就提到列表是无法直接进行数学运算的，一旦将列表转换为数组后，就可以实现各种常见的数学运算，如四则运算、比较运算、广播运算等。

2.1 四则运算

在numpy模块中，实现四则运算的计算既可以使用运算符号，也可以使用函数，具体如下例所示：

# 加法运算
math = np.array([98,83,86,92,67,82])
english = np.array([68,74,66,82,75,89])
chinese = np.array([92,83,76,85,87,77])
tot_symbol = math+english+chinese
tot_fun = np.add(np.add(math,english),chinese)
print('符号加法：\n',tot_symbol)
print('函数加法：\n',tot_fun)

# 除法运算
height = np.array([165,177,158,169,173])
weight = np.array([62,73,59,72,80])
BMI_symbol = weight/(height/100)**2
BMI_fun = np.divide(weight,np.divide(height,100)**2)
print('符号除法：\n',BMI_symbol)
print('函数除法：\n',BMI_fun)

结果：

符号加法：
 [258 240 228 259 229 248]
函数加法：
 [258 240 228 259 229 248]
符号除法：
 [22.77318641 23.30109483 23.63403301 25.20920136 26.7299275 ]
函数除法：
 [22.77318641 23.30109483 23.63403301 25.20920136 26.7299275 ]

四则运算中的符号分别是“±*/”，对应的numpy模块函数分别是np.add、np. subtract、np.multiply和np.divide。需要注意的是，函数只能接受两个对象的运算，如果需要多个对象的运算，就得使用嵌套方法，如上所示的符号加法和符号除法。不管是符号方法还是函数方法，都必须保证操作的数组具有相同的形状，除了数组与标量之间的运算（如除法中的身高与100的商）。另外，还有三个数学运算符，分别是余数、整除和指数：

arr7 = np.array([[1,2,10],[10,8,3],[7,6,5]])
arr8 = np.array([[2,2,2],[3,3,3],[4,4,4]])
print('数组arr7：\n',arr7)
print('数组arr8：\n',arr8)
# 求余数
print('计算余数：\n',arr7 % arr8)
# 求整除
print('计算整除：\n',arr7 // arr8)
# 求指数
print('计算指数：\n',arr7 ** arr8)

结果：

数组arr7：
 [[ 1  2 10]
 [10  8  3]
 [ 7  6  5]]
数组arr8：
 [[2 2 2]
 [3 3 3]
 [4 4 4]]
计算余数：
 [[1 0 0]
 [1 2 0]
 [3 2 1]]
计算整除：
 [[0 1 5]
 [3 2 1]
 [1 1 1]]
计算指数：
 [[   1    4  100]
 [1000  512   27]
 [2401 1296  625]]

# 整除部分
np.modf(arr7/arr8)[1]

结果：

array([[0., 1., 5.],
       [3., 2., 1.],
       [1., 1., 1.]])

可以使用“%、//、**”计算数组元素之间商的余数、整除部分以及数组元素之间的指数。当然，如果读者比较喜欢使用函数实现这三种运算的话，可以使用np.fmod、np.modf和np.power，但是整除的函数应用会稍微复杂一点，需要写成np.modf(arr7/arr8)[1]，因为modf可以返回数值的小数部分和整数部分，而整数部分就是要取的整除值。

2.2 比较运算

除了数组的元素之间可以实现上面提到的数学运算，还可以做元素间的比较运算。关于比较运算符有表1所示的六种情况。

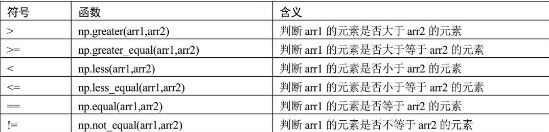
运用比较运算符可以返回bool类型的值，即True和False。在笔者看来，有两种情况会普遍使用到比较运算符，一个是从数组中查询满足条件的元素，另一个是根据判断的结果执行不同的操作。例如：

# 取子集
# 从arr7中取出arr7大于arr8的所有元素
print(arr7)
print('满足条件的二维数组元素获取：\n',arr7[arr7>arr8])
# 从arr9中取出大于10的元素
arr9 = np.array([3,10,23,7,16,9,17,22,4,8,15])
print('满足条件的一维数组元素获取：\n',arr9[arr9>10])

# 判断操作
# 将arr7中大于7的元素改成5，其余的不变
print('二维数组的条件操作：\n',np.where(arr7>7,5,arr7))
# 将arr9中大于10 的元素改为1，否则改为0
print('一维数组的条件操作：\n',np.where(arr9>10,1,0))

结果：

[[ 1  2 10]
 [10  8  3]
 [ 7  6  5]]
满足条件的二维数组元素获取：
 [10 10  8  7  6  5]
满足条件的一维数组元素获取：
 [23 16 17 22 15]
二维数组的条件操作：
 [[1 2 5]
 [5 5 3]
 [7 6 5]]
一维数组的条件操作：
 [0 0 1 0 1 0 1 1 0 0 1]

运用bool索引，将满足条件的元素从数组中挑选出来，但不管是一维数组还是多维数组，通过bool索引返回的都是一维数组；np.where函数与Excel中的if函数一样，就是根据判定条件执行不同的分支语句。

2.3 广播运算

前面所介绍的各种数学运算符都是基于相同形状的数组，当数组形状不同时，也能够进行数学运算的功能称为数组的广播。但是数组的广播功能是有规则的，如果不满足这些规则，运算时就会出错。数组的广播规则是：

• 各输入数组的维度可以不相等，但必须确保从右到左的对应维度值相等。
• 如果对应维度值不相等，就必须保证其中一个为1。
• 各输入数组都向其shape最长的数组看齐，shape中不足的部分都通过在前面加1补齐。

从字面上理解这三条规则可能比较困难，下面通过几个例子对每条规则加以说明，希望能够帮助读者理解它们的含义：

# 各输入数组维度一致，对应维度值相等
arr10 = np.arange(12).reshape(3,4)
arr11 = np.arange(101,113).reshape(3,4)
print('3×4的二维矩阵运算：\n',arr10 + arr11)
# 各输入数组维度不一致，对应维度值相等
arr12 = np.arange(60).reshape(5,4,3)
arr10 = np.arange(12).reshape(4,3)
print('维数不一致，但末尾的维度值一致：\n',arr12 + arr10)
# 各输入数组维度不一致，对应维度值不相等，但其中有一个为1
arr12 = np.arange(60).reshape(5,4,3)
arr13 = np.arange(4).reshape(4,1)
print('维数不一致，维度值也不一致，但维度值至少一个为1：\n',arr12 + arr13)
# 加1补齐
arr14 = np.array([5,15,25])
print('arr14的维度自动补齐为(1,3)：\n',arr10 + arr14)

结果：

3×4的二维矩阵运算：
 [[101 103 105 107]
 [109 111 113 115]
 [117 119 121 123]]
维数不一致，但末尾的维度值一致：
 [[[ 0  2  4]
  [ 6  8 10]
  [12 14 16]
  [18 20 22]]

 [[12 14 16]
  [18 20 22]
  [24 26 28]
  [30 32 34]]

 [[24 26 28]
  [30 32 34]
  [36 38 40]
  [42 44 46]]

 [[36 38 40]
  [42 44 46]
  [48 50 52]
  [54 56 58]]

 [[48 50 52]
  [54 56 58]
  [60 62 64]
  [66 68 70]]]
维数不一致，维度值也不一致，但维度值至少一个为1：
 [[[ 0  1  2]
  [ 4  5  6]
  [ 8  9 10]
  [12 13 14]]

 [[12 13 14]
  [16 17 18]
  [20 21 22]
  [24 25 26]]

 [[24 25 26]
  [28 29 30]
  [32 33 34]
  [36 37 38]]

 [[36 37 38]
  [40 41 42]
  [44 45 46]
  [48 49 50]]

 [[48 49 50]
  [52 53 54]
  [56 57 58]
  [60 61 62]]]
arr14的维度自动补齐为(1,3)：
 [[ 5 16 27]
 [ 8 19 30]
 [11 22 33]
 [14 25 36]]

如上结果所示，第一个打印结果其实并没有用到数组的广播，因为这两个数组具有同形状；第二个打印结果是三维数组和两维数组的和，虽然维数不一样，但末尾的两个维度值是一样的，都是4和3，最终得到5×4×3的数组；第三个打印中的两个数组维数和维度值均不一样，但末尾的两个维度值中必须含一个1，且另一个必须相同，都为4，相加之后得到5×4×3的数组；第四个打印结果反映的是4×3的二维数组和(3,)的一维数组的和，两个数组维度不一致，为了能够运算，广播功能会自动将(3,)的一维数组补齐为(1,3)的二维数组，进而得到4×3的数组。通过对上面例子的解释，希望读者能够掌握数组广播功能的操作规则，以防数组运算时发生错误。

3、常用的数学和统计函数

numpy模块的核心就是基于数组的运算，相比于列表或其他数据结构，数组的运算效率是最高的。在统计分析和挖掘过程中，经常会使用到numpy模块的函数，接下来将常用的数学函数和统计函数汇总到表2中，以便读者查询和使用。

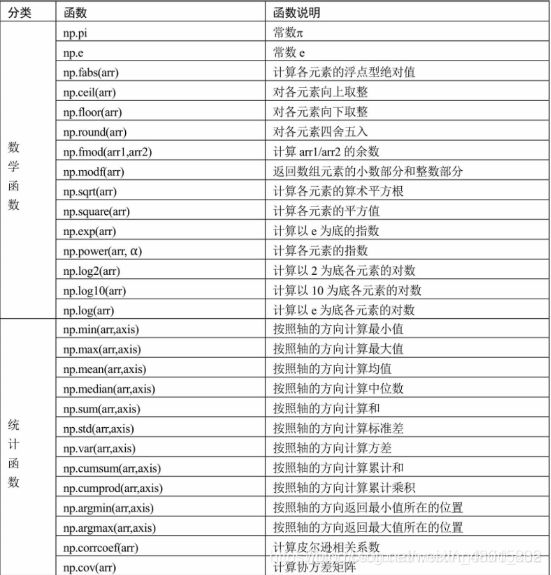
根据上面的表格，需要对统计函数重点介绍，这些统计函数都有axis参数，该参数的目的就是在统计数组元素时需要按照不同的轴方向计算，如果axis=1，则表示按水平方向计算统计值，即计算每一行的统计值；如果axis=0，则表示按垂直方向计算统计值，即计算每一列的统计值。为了简单起见，这里做一组对比测试，以便读者明白轴的方向具体指什么：

arr4 = np.array([[1,10,100],[2,20,200],[3,30,300]])
print(arr4)
print('垂直方向计算数组的和：\n',np.sum(arr4,axis = 0))
print('水平方向计算数组的和：\n',np.sum(arr4, axis = 1))

结果：

[[  1  10 100]
 [  2  20 200]
 [  3  30 300]]
垂直方向计算数组的和：
 [  6  60 600]
水平方向计算数组的和：
 [111 222 333]

如上结果所示，垂直方向就是对数组中的每一列计算总和，而水平方向就是对数组中的每一行计算总和。同理，如果读者想小试牛刀的话，就以4.1.3节中读取的学生考试成绩为例，计算每一个学生（水平方向）的总成绩和每一门科目（垂直方向）的平均分。

4、线性代数的相关计算

数据挖掘的理论背后几乎离不开有关线性代数的计算问题，如矩阵乘法、矩阵分解、行列式求解等。本章介绍的numpy模块同样可以解决各种线性代数相关的计算，只不过需要调用Numpy的子模块linalg（线性代数的缩写），该模块几乎提供了线性代数所需的所有功能。
表3给出了一些numpy模块中有关线性代数的重要函数，以便读者快速查阅和掌握函数用法。

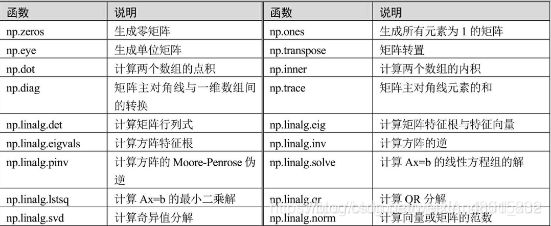
4.1 矩阵乘法

# 一维数组的点积
vector_dot = np.dot(np.array([1,2,3]), np.array([4,5,6]))
print('一维数组的点积：\n',vector_dot)
# 二维数组的乘法
print('两个二维数组：')
print(arr10)
print(arr11)
arr2d = np.dot(arr10,arr11)
print('二维数组的乘法：\n',arr2d)

结果：

一维数组的点积：
 32
两个二维数组：
[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]
[[101 102 103 104]
 [105 106 107 108]
 [109 110 111 112]]
二维数组的乘法：
 [[ 323  326  329  332]
 [1268 1280 1292 1304]
 [2213 2234 2255 2276]
 [3158 3188 3218 3248]]

点积函数dot，使用在两个一维数组中，实际上是计算两个向量的乘积，返回一个标量；使用在两个二维数组中，即矩阵的乘法，矩阵乘法要求第一个矩阵的列数等于第二个矩阵的行数，否则会报错。

4.2 diag函数的使用

# diag的使用
arr15 = np.arange(16).reshape(4,-1)
print('4×4的矩阵：\n',arr15)
print('取出矩阵的主对角线元素：\n',np.diag(arr15))
print('由一维数组构造的方阵：\n',np.diag(np.array([5,15,25])))

结果：

4×4的矩阵：
 [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]
取出矩阵的主对角线元素：
 [ 0  5 10 15]
由一维数组构造的方阵：
 [[ 5  0  0]
 [ 0 15  0]
 [ 0  0 25]]

如上结果所示，如果给diag函数传入的是二维数组，则返回由主对角元素构成的一维数组；如果向diag函数传入一个一维数组，则返回方阵，且方阵的主对角线就是一维数组的值，方阵的非主对角元素均为0。

4.3 特征根与特征向量

我们知道，假设A为n阶方阵，如果存在数λ和非零向量，使得Ax=λx（x≠0），则称λ为A的特征根，x为特征根λ对应的特征向量。如果需要计算方阵的特征根和特征向量，可以使用子模块linalg中的eig函数：

# 计算方阵的特征向量和特征根
arr16 = np.array([[1,2,5],[3,6,8],[4,7,9]])
print('计算3×3方阵的特征根和特征向量：\n',arr16)
print('求解结果为：\n',np.linalg.eig(arr16))

结果：

计算3×3方阵的特征根和特征向量：
 [[1 2 5]
 [3 6 8]
 [4 7 9]]
求解结果为：
 (array([16.75112093, -1.12317544,  0.37205451]), array([[-0.30758888, -0.90292521,  0.76324346],
       [-0.62178217, -0.09138877, -0.62723398],
       [-0.72026108,  0.41996923,  0.15503853]]))

如上结果所示，特征根和特征向量的结果存储在元组中，元组的第一个元素就是特征根，每个特征根对应的特征向量存储在元组的第二个元素中。

4.4 多元线性回归模型的解

多元线性回归模型一般用来预测连续的因变量，如根据天气状况预测游客数量、根据网站的活动页面预测支付转化率、根据城市人口的收入、教育水平、寿命等预测犯罪率等。该模型可以写成Y=Xβ+ε，其中Y为因变量，X为自变量，ε为误差项。要想根据已知的X来预测Y的话，必须得知道偏回归系数β的值。对于熟悉多元线性回归模型的读者来说，一定知道偏回归系数的求解方程，即β=(X’X)-1X’Y)。

# 计算偏回归系数
X = np.array([[1,1,4,3],[1,2,7,6],[1,2,6,6],[1,3,8,7],[1,2,5,8],[1,3,7,5],[1,6,10,12],[1,5,7,7],[1,6,3,4],[1,5,7,8]])
Y = np.array([3.2,3.8,3.7,4.3,4.4,5.2,6.7,4.8,4.2,5.1])

X_trans_X_inverse = np.linalg.inv(np.dot(np.transpose(X),X))
beta = np.dot(np.dot(X_trans_X_inverse,np.transpose(X)),Y)
print('偏回归系数为：\n',beta)

结果：

偏回归系数为：
 [1.78052227 0.24720413 0.15841148 0.13339845]

如上所示，X数组中，第一列全都是1，代表了这是线性回归模型中的截距项，剩下的三列代表自变量，根据β的求解公式，得到模型的偏回归系数，从而可以将多元线性回归模型表示为Y=1.781+0.247x1+0.158x2+0.133x3。

4.5 多元一次方程组的求解

在中学的时候就学过有关多元一次方程组的知识，例如《九章算术》中有一题是这样描述的：今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗；问上、中、下禾实秉各几何？解答这个问题就需要应用三元一次方程组，该方程组可以表示为：

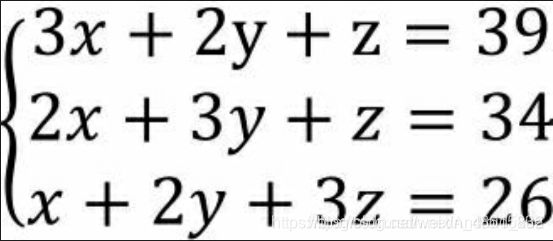
在线性代数中，这个方程组就可以表示成AX=b, A代表等号左边数字构成的矩阵，X代表三个未知数，b代表等号右边数字构成的向量。如需求解未知数X，可以直接使用linalg子模块中的solve函数，具体代码如下：

# 多元线性方程组
A = np.array([[3,2,1],[2,3,1],[1,2,3]])
b = np.array([39,34,26])
X = np.linalg.solve(A,b)
print('三元一次方程组的解：\n',X)

结果：

三元一次方程组的解：
 [9.25 4.25 2.75]

如上结果所示，得到方程组x、y、z的解分别是9.25、4.25和2.75。

4.6 范数的计算

范数常常用来度量某个向量空间（或矩阵）中的每个向量的长度或大小，它具有三方面的约束条件，分别是非负性、齐次性和三角不等性。最常用的范数就是p范数，其公式可以表示成‖x‖p=(|x1|p+|x2|p+…+|xn|p)1/p。关于范数的计算，可以使用linalg子模块中的norm函数，举例如下：

# 范数的计算
arr17 = np.array([1,3,5,7,9,10,-12])
# 一范数
res1 = np.linalg.norm(arr17, ord = 1)
print('向量的一范数：\n',res1)
# 二范数
res2 = np.linalg.norm(arr17, ord = 2)
print('向量的二范数：\n',res2)
# 无穷范数
res3 = np.linalg.norm(arr17, ord = np.inf)
print('向量的无穷范数：\n',res3)

结果：

向量的一范数：
 47.0
向量的二范数：
 20.223748416156685
向量的无穷范数：
 12.0

如上结果所示，向量的无穷范数是指从向量中挑选出绝对值最大的元素。

5、伪随机数的生成

虽然在Python内置的random模块中可以生成随机数，但是每次只能随机生成一个数字，而且随机数的种类也不够丰富。如果读者想一次生成多个随机数，或者在内置的random模块中无法找到所需的分布函数，作者推荐使用numpy模块中的子模块random。关于各种常见的随机数生成函数，可见表4，以供读者查阅。

读者可能熟悉上面的部分分布函数，但并不一定了解它们的概率密度曲线。为了直观展现分布函数的概率密度曲线，这里以连续数值的正态分布和指数分布为例进行介绍。如果读者想绘制更多其他连续变量的分布概率密度曲线，可以对如下代码稍做修改。

import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
# 生成各种正态分布随机数
np.random.seed(1234)
rn1 = np.random.normal(loc = 0, scale = 1, size = 1000)
rn2 = np.random.normal(loc = 0, scale = 2, size = 1000)
rn3 = np.random.normal(loc = 2, scale = 3, size = 1000)
rn4 = np.random.normal(loc = 5, scale = 3, size = 1000)
# 绘图
plt.style.use('ggplot')
sns.distplot(rn1, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {
     'color':'black','label':'u=0,s=1','linestyle':'-'})
sns.distplot(rn2, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {
     'color':'red','label':'u=0,s=2','linestyle':'--'})
sns.distplot(rn3, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {
     'color':'blue','label':'u=2,s=3','linestyle':':'})
sns.distplot(rn4, hist = False, kde = False, fit = stats.norm, 
             fit_kws = {
     'color':'purple','label':'u=5,s=3','linestyle':'-.'})
# 呈现图例
plt.legend()
# 呈现图形
plt.show()

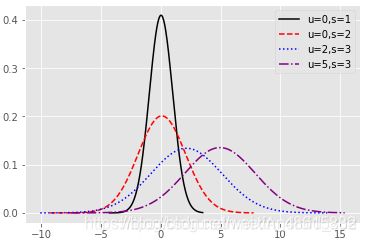
如图1所示，呈现的是不同均值和标准差下的正态分布概率密度曲线。当均值相同时，标准差越大，密度曲线越矮胖；当标准差相同时，均值越大，密度曲线越往右移。

# 生成各种指数分布随机数
np.random.seed(1234)
re1 = np.random.exponential(scale = 0.5, size = 1000)
re2 = np.random.exponential(scale = 1, size = 1000)
re3 = np.random.exponential(scale = 1.5, size = 1000)
# 绘图
sns.distplot(re1, hist = False, kde = False, fit = stats.expon, 
             fit_kws = {
     'color':'black','label':'lambda=0.5','linestyle':'-'})
sns.distplot(re2, hist = False, kde = False, fit = stats.expon, 
             fit_kws = {
     'color':'red','label':'lambda=1','linestyle':'--'})
sns.distplot(re3, hist = False, kde = False, fit = stats.expon, 
             fit_kws = {
     'color':'blue','label':'lambda=1.5','linestyle':':'})
# 呈现图例
plt.legend()
# 呈现图形
plt.show()

图2展现的是指数分布的概率密度曲线，通过图形可知，指数分布的概率密度曲线呈现在y=0的右半边，而且随着lambda参数的增加，概率密度曲线表现得越矮，同时右边的“尾巴”会更长而厚。

6、小结

本文介绍了有关数值计算的numpy模块，包括数组的创建、基本操作、数学运算、常用的数学和统计函数、线性代数以及随机数的生成。通过本章内容的学习，希望能够为读者在之后的数据分析和挖掘方面的学习打下基础。
下面对本章中涉及的Python函数进行汇总，主要是正文中没有写入表格的函数，以便读者查询和记忆。