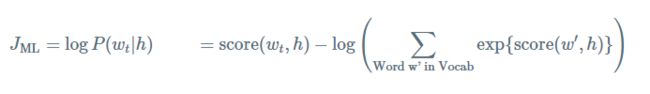word2vec模型

word2vec

动机：为什么要学习词向量(Word Embeddings)

传统的自然语言处理系统把词(word)当作一个离散的原子符号。比如，猫可以使用Id537来表示，Id143表示狗。这些编码是任意的，这些编码对于系统处理不同的单词并没有提供有用的信息。这就意味着，如果系统已经学习了什么是“猫”的信息，但这个系统处理什么是“狗”是并没有提供很大的帮助(比如：他们都是动物，有四条腿，宠物，等)。这种词的表示是独立的，离散的Id使得数据之间并没有很大的关联，通常也意味着我们需要更多的数据去成功的训练统计模型。然而，向量(vector representation)克服了这些缺点。

向量空间模型(Vector space models, VSMs)使用一个连续的空间表示词(words/embed), 它把语义相关的单词都映射在了附近为位置。在NLP中，VSM拥有很长很丰富的历史，但是所有的方法，在很大的程度上都有这些或者那样的分布式假设(Distributional Hypothesis), 及指出了出现在相同上下文的词具有相同的语意。基于这种假设可以划分两种不同的类别：count-based methods e.g. Latent Semantic Analysis), 和 predictive methods (e.g. neural probabilistic language models)

Baroni et al详细的介绍了这两种方法的差异性。但是总的来说，Count-based methods compute the statistics of how often some word co-occurs with its neighbor words in a large text corpus, and then map these count-statistics down to a small, dense vector for each word(只可意会不可言传啊! ^_^)。就学习更小，更稠密词向量(dense embedding vectors)而言, Predictive models直接从它附近的词去预测它。

从最原始的文本去学习词向量，Word2vec是一个特别有效的预测模型(Predictive models)。它具有两个版本，Continuous Bag-of-Words 模型(CBOW) 和 Skip-Gram 模型。从算法的角度来看，这两个模型都是相似的。

CBOW模型是给定周围的上下文预测(surrounding context)一个中心词(center word)。比如，给定“The cat sits on the mat”, 我们把[“The” , “cat”, “sits”, “on”, “mat”]为上下文，而我们需要去预测和生成的中心词为”jumped”。

Skip-Gram模型：是给定中心词预测它周围的词，它与CBOW模型刚好是相反的。

对于这两种模型，对于数据集比较小的情况CBOW性能要比Skip-Gram模型好，但是对于数据集比较大时，其性能要差一些。

Scaling up with Noise-Contrastive Training

给定前面的词(previous words)的概率 h (for “history”) 来预测下一个词的概率 wt (for “target”)，为了最大化预测概率传统的神经网络概率语言模型都是使用最大似然(maximum likelihood ML)来进行训练，以softmax 函数为例：

其中 score(wt,h) 表示单词 wt 与上下文 h 的相容性。通过在训练集求解最大log似然来训练该模型。比如，最大化

上面等式为正确标准化的语言模型。然而训练它，代价非常的大。因为每个训练，我对于给定当前的上下文 h , 我们需要使用score去计算和标准化在语料库 V 中所有其他的单词 w′ 。

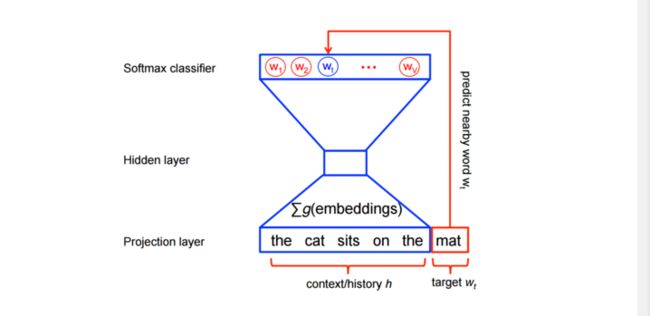
换句话说，特征学习对于word2vec模型并不需要一个完全的概率模型。及对于相同的上下文，CBOW 和 skip-gram 模型训练使用二分类目标函数(binary classification objective)从 k 个假想(imaginary/noise)词 w^ 中判别出真实的目标词 wt 。CBOW模型可以使用下图来描述，对于skip-gram模型只需要简单的把方向反转一下。

数学表示为，对于每个词最大化目标函数为：

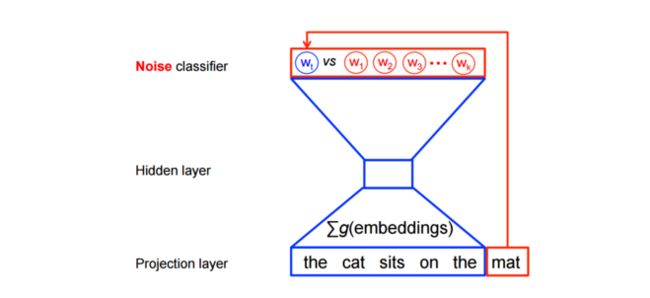
其中， Qθ(D=1|w,h) 表示二分类logistic 回归概率(binary logistic regression probability)在数据集 D 上，模型已知单词 w 在上下文 h 中，需要学习(或者说计算)的是词向量 θ 。在实践中，我们通过噪音分布(noise distribution)近似抽取k个constrastive words。

因此，目标变成了最大化真实词(real words)的概率，最小化噪音词(noise)的概率。从技术的角度，这称之为负采样(Negative Sampling)。使用这个损失函数有一个很好数学动机：在有限的条件下所提出的更新规则近似的更新了softmax函数。但是计算特别的具有吸引力，因为现在计算这个损失函数我们仅仅需要规格化我们所选择的 k 个早因此，而不是整个词汇表 V ，这使得训练它更快。

让我们更加直观的看这个模型在实践中是怎么工作的。

Skip-gram 模型详解

考虑数据集

the quick brown fox jumped over the lazy dog

首先，我们形成单词的数据集和上下文，我们可以使用任何有意义的方式定义”上下文”。事实上，我们都知道语法规则(当前目标词的语法依赖关系)。因为，我们可以定义“上下文”(context)为为这词左边窗口的单词，而目标词(target word)作为右边的单词。假设窗口(window size)为1。对于上面数据集的(context, target)对为，

（[the, brown], quick), ([quick, fox], brown), ([brown, jumped], fox), …

我们知道skip-gram模型是给定context去预测目标词。所以这任务就变成了预测‘the’ 和 ‘brown’给定‘quick’，预测‘quick’和’fox’ 给定 ‘brown’，等。因为数据集的(input, output)对为

(quick, the), (quick brow), (brown, quick), (brow, fox), …

其中目标函数是定义在整个数据集上，但是我们可以是使用随机梯度递减(stochastic gradient descent, SGD)来进行优化, 每一次只使用一个例子。(或者使用batch_size个例子中的minibatch个, 一般情况下， 16≤batch−size≤512 )。下面一步一步的讲解这个过程是如何工作的。

假设上面第一个训练例子(quick, the)在第t步下进行训练, 及预测the给定input。我们选择 num−noise noisy example通过一些noise distribution, 一般使用unigram ditribution( P(w) )。为了简单化，假设 num−noise=1 和选择sheep作为noisy example。那么在第t 目标函数为
J(t)NEG=logQθ(D=1|the,quick)+logQθ(D=0|sheep,quick)

及目标是就去更新向量参数 θ 使得目标函数最大化。为了达到这个目的我们可以通过目标函数对向量参数 θ 进行求导，及 ∂∂θJNEG ,然后沿着梯度的方向更行向量参数。这个过程一直在训练集上重复计算，这就使得每个单词的向量表示进行了更新，直到但这个模型可以成功的从noise words中判断出real words。

我们可以使用像 t-SNE dimensionality reduction technique将所学习到的词向量投影到2维空间上。当我们仔细看这个可视化试图的，这向量捕获了非常有用的语义信息。在语义的关系上，我们也发现了一些确定的方向在可视化向量空间上。如下图所示

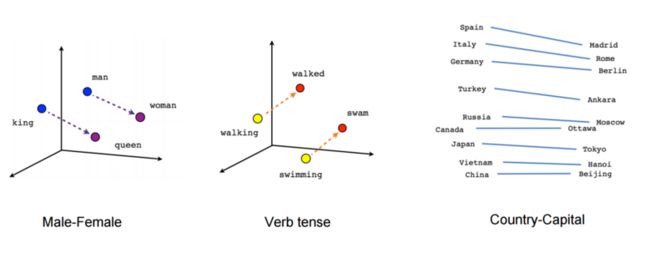
这个例子说明了为什么向量表示对于许多的NLP任务是非常的有用，比如说，词性标注，命名实体识别, etc。

对于CBOW模型来说我们只需要把上面的(context, target)对换一下。其过程还是一样的

Skip-Gram 模型数学表示

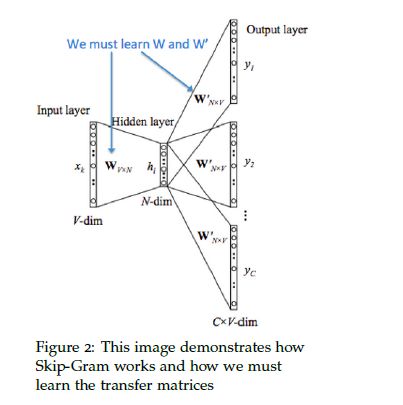
首先，来定义一些数学符号
1. 输入one-hot向量或者context使用 x(i) 表示。
2. 输出使用 y(i) 进行表示。
3. 输入向量矩阵 W1∈Rn×|V| , n,|V| 分别表示向量的大小和词汇表的大小
4. wi 表示词汇表的第 i 个单词
5. ui 表示 W(1) 的第 i 列，及单词 w(i) 的输入向量表示
6. W(2)∈Rn times|V| 表示输出向量矩阵
7. v(i) 表示 W(2) 的第 i 行，及单词 w(1) 的输出向量表示。

则，Skip-Gram可以使用下面六步来表示，
1. 生成one-hot 输入向量 x
2. 获取输入向量 u(i)=W(1)x
3. 因为不需要averaging(或者可以理解为，不需要对输入数据规格化)，因此 h=u(i) 。
4. 使用 v=W(2)h 生成2C个score vectors, v(i−C),...,v(i−1),v(i+1),...,v(i+C) ，其中 C 为context的大小
5. 将每个score vectors 转换成概率， y=softmax(x)
6. 应该使得说生成的概率要近似等于真实的概率，及 y(i−C),...,y(i−1),y(i+1),...,y(i+C)

我们的目标是最小化，损失函数啊：
mini J=−logP(context|target)

注意与前面区别， 前面少了一个负号，因此是最大损失函数
其给定输入向量 r^ (也就是target)，使用softmax的word2vec模型为
Pr(wordi|r^,w)=exp(wTir^)∑|V|j=1exp(wTjr^)
其中 wj 表示词汇表里所有单词的输出向量(context)。

方法一：如果使用Cross-Entropy 那么损失函数为：

因为该方法每次都需要对词汇表中所有的单词都进行更新，因此训练速度非常的慢

Jce=−logPr(wordi|r^,w)=−wTr^+log∑|V|j=1exp(wTjr^)

为了是损失函数最小化，可以使用梯度下降的方法来进行计算,及相应的梯度为：
∂Jce∂r^=−wi+∑k=1|V|Pr(wordk|r^,w)wk

∂Jce∂wj=−r^(j=i)+exp(wTjr^)r^∑|V|k=1exp(wTkr^)

方法二：使用负采样方法，损失函数为：

Jng=−logσ(wTir^)−∑Kk=1log(σ(−wTkr^))

其中， r^ 表示输入向量(target), wi 表示输出向量(context), wk 表示noisy word及K个负样本。

相应梯度为:

∂Jng∂r^=wi∗(σ(wTi)−1)+∑Kk=1wk(1−σ(−wTkr^))

∂Jne∂wj=⎧⎩⎨⎪⎪r^(σ(wTir^)−1)−r^(σ(−wTjr^)−1)0if j=iif j≠i,j∈{1,...,K}其他

其中 ∗ 表示element-wise product

整理翻译以下内容
1. tensorflow Vector Representations of Words
2. CS224d: Deep Learning for Natural Language Processing

仅作学习交流使用，严禁用于商业目的，转载请说明出处！