二分图的判定，最大匹配

<1>.什么是二分图

如果一个图的顶点可以分为两个集合X和Y，图的所有边一定是有一个顶点属于集合X，另一个顶点属于集合Y，则称该图为“二分图”（ Bipartite Graph ）

 

 

 

 

<2>.二分图的判定

 

• 如果一个图是连通的，可以用如下的方法判定是否是二分图：

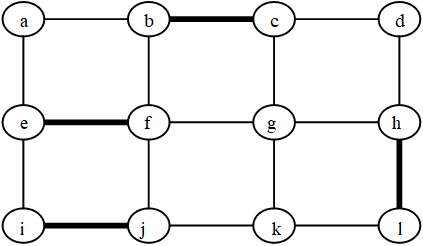
• 在图中任选一顶点v，定义其距离标号为0，然后把它的邻接点的距离标号均设为1，接着把所有标号为1的邻接点均标号为2（如果该点未标号的话），如图所示，以此类推。

• 标号过程可以用一次BFS实现。标号后，所有标号为奇数的点归为X部，标号为偶数的点归为Y部。

• 接下来，二分图的判定就是依次检查每条边，看两个端点是否是一个在X部，一个在Y部。

（如果一个图不连通则在每个连通块中作判定）

 



算法实现；

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

 

 

 

 

 

 

<3>.最大匹配

 

 

匹配定义； 令G（V，E） 是一个无向图，若存在边集M ，使得M中所有的边都没有公共顶点，则称M是G的一个匹配（matching）。

 

最大匹配；边数最多的匹配称为最大匹配

 

完美匹配；,如果所有的点都在匹配边上，称这个最大匹配是完美匹配

 

 

增广路径

如果P是图G中一条连通两个未匹配顶点的路径（P以未匹配点为起点和终点的路径），并且属M的边和不属于M的边（即已匹配和待匹配的边）在P上交替出现，则称P为现对于M的一条增广路径

 

二分图的最大匹配-增广路径

令M是G的一个匹配，则P是M的一条增广路径；则是G的一个大小为|M|+1的匹配。





新增的边或者是M的边，或者是P的边，但不是即在M的边，也在P的边。

 

举例；



边集；M={（b,c）,（e,f）,（i,j），（h,l）}  

 

 

 



 



 



 

 

 

 

推出三个结论；

1）P的路径长度必定为奇数，第一条边和最后一条边都不属于M

2）P经过取反操作可以得到一个更大的匹配M

3) M为G的最大匹配当且仅当不存在相对于M的增广路径

 

 

 

 

 

 

 

<4>.匈牙利算法（求二分图的最大匹配）

 

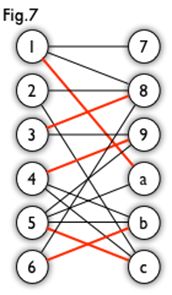
<匈牙利树>；一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 1，可以得到如图 2的一棵 BFS 树，如果所有的叶子都是匹配点，则这课BFS树是匈牙利树 

 

 

 

算法实现

(1). 置M（匹配）为空

(2). 找出一条增广路径P，通过取反操作获得更大的匹配M’代替M

(3). 重复(2)操作直到找不出增广路径为止。

 

>>>细节

对于二分图A侧（可以把点少的一侧看作A侧）的每个点，依次如下操作：

1.设置A[i]为当前点。

2.用A侧和B侧的点轮流进行如下操作。

（1）对A侧的点A[i]：找到一条没有匹配的边。如果边的B侧的点不属于匹配中另外的边，那么这个时候表示增广路径找到了（初始情况下直接相连的一条边的最大匹配就属于这种情况），修改最大匹配。如果边的B侧的点属于匹配中另外的边，设B侧的点为B[j]，则进入（2）。如果这些都做不到，需要进行回溯。如果回溯到了起点，表明从起点A[i]找增广路径失败了。注意，能否找到增广路径全由A侧的点决定（找边和回溯），B侧的点做的操作非常简单。

（2）对B侧的点B[j]，由于是找增广路径，已匹配的边需要用到，故直接找到B[j]所在的匹配边在A侧对应的点A[k]，把A[k]置为当前点继续进行步骤（1）。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include