【网络流】最大流：上界可行流，多源汇，关键边

上下界可行流

无源汇上下界可行流

原题链接

可行流满足：

①流量守恒

②容量限制：$c_l(u,v)\le f(u,v)\le c_u(u,v)$

与一般的可行流不同的是，某一边流量有给定的上下界。

建图：流网络为$G$，$G$中的某一个可行流记为$f$，无源点与汇点，且有上下界。

对于$(G,f)$，我们要建立一个$(G^{\prime },f^{\prime })$与$(G,f)$对应，且为正常的流网络，有源点和汇点，只有上界没有下界。

对于$f$中的某一条边$(u,v)$，有流量上界$c_u(u,v)$，流量下界$c_l(u,v)$，流量记为$f(u,v)$，满足$c_l(u,v)\le f(u,v)\le c_u(u,v)$，且可以转化为$0\le f(u,v)-c_l(u,v)\le c_u(u,v)-c_l(u,v)$，符合只有上界没有下界。

①在可行流中，将所有边的流量都减去边的容量下界。

②让新网络中的容量$c(u,v)$等于原网络中的流量上界流容量下界。

因为$f^{\prime }(u,v)=f(u,v)-c_{l}l(u,v)$，因此满足容量限制，但不一定满足流量守恒。

对于点$x$，由于流量都要减去流量下界，因此流出的流量减少了$c_{出}={\sum }_{x\in V}{c}_l(x,v)$，流入的流量减少了$c_{入}={\sum }_{x\in V}{c}_l(v,x)$。

若$c_{入}\ne c_{出}$，则流量不守恒。

（i）若$c_{入}>c_{出}$，则从$s$到$x$连一条容量为$c_{入}-c_{出}$的边。

（ii）若$c_{入}<c_{出}$，则从$x$到$t$连一条容量为$c_{出}-c_{入}$的边。

因此既满足了流量守恒，又添加了源点与汇点。构造出来的流网络$G^{\prime }$称为我们所熟悉的流网络。

若想流量守恒，那么从$s$所出去的边的流量必须取满，所以$f^{\prime }$必然为$G^{\prime }$的最大流。

• 在建图的同时，可以验证这种构图方式是正确的，即原流网络的可行流与新流网络的最大流一一对应（$(G,f)\iff (G^{\prime },f^{\prime })$）。

代码如下：

#include
using namespace std;

const int N=200+10;
const int M=30000+10;
const int INF=1e9;

int n,m,S,T;
int h[N],ve[M],c[M],l[M]/*记容量下界*/,ne[M],id;
int q[N],d[N],cur[N],A[N]/*记录每个点的所有入边的容量下界之和减去出边的容量下界之和的差*/;

void add(int x,int y,int cl,int cu){
    ve[id]=y;c[id]=cu-cl;l[id]=cl;ne[id]=h[x];h[x]=id++;
    ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}

bool bfs(){
    int he=0,ta=0;
    memset(d,-1,sizeof d);
    q[0]=S;d[S]=0;cur[S]=h[S];
    
    while(he<=ta){
        int x=q[he++];
        
        for(int i=h[x];~i;i=ne[i]){
            int y=ve[i];
            
            if(d[y]==-1&&c[i]){
                d[y]=d[x]+1;
                cur[y]=h[y];
                if(y==T)return true;
                q[++ta]=y;
            }
        }
    }
    return false;
}

int dfs(int u,int limit){
    if(u==T)return limit;
    int flow=0;
    
    for(int i=cur[u];~i&&flow0)add(S,i,0,A[i]),tot+=A[i];
        else if(A[i]<0)add(i,T,0,-A[i]);
        
    if(dinic()!=tot)puts("NO");
    else{
        puts("YES");
        
        for(int i=0;i

有源汇上下界最大流

原题链接

与上题不同的是：①给出的流网络有源点与汇点；②求的不是可行流，而是最大可行流。

• 有源汇$\to$无源汇：可以从$t$向$s$连一条容量是$+\infty$的边，那么对于$s,t$而言就是流量守恒的。如此操作就可以将整张图变成一张无源汇的流网络。就可以用上一题的方法做。

题目所让我们求的是原源汇之间的最大可行流。

①先用上题的方式构造$G^{\prime }$，每条边$c(u,v)=c_u(u,v)-c_l(u,v)$，再建虚拟源点与汇点$S,T$，并增加一条从$t$向$s$连一条容量是$+\infty$的边。

②求完一遍满流后，在残留网络里先删除$t\to s$的边，删完之后求$s\to t$的最大可行流。

③求的最大流加上原网络的流量就是所要求的最大流量。

代码如下：

#include
using namespace std;

const int N=200+10;
const int M=30000+10;
const int INF=1e9;

int n,m,S,T;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N],A[N];

void add(int x,int y,int z){
    ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
    ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}

bool bfs(){
    int he=0,ta=0;
    memset(d,-1,sizeof d);
    q[0]=S;d[S]=0;cur[S]=h[S];
    
    while(he<=ta){
        int x=q[he++];
        
        for(int i=h[x];~i;i=ne[i]){
            int y=ve[i];
            
            if(d[y]==-1&&c[i]){
                d[y]=d[x]+1;
                cur[y]=h[y];
                if(y==T)return true;
                q[++ta]=y;
            }
        }
    }
    return false;
}

int dfs(int u,int limit){
    if(u==T)return limit;
    int flow=0;
    
    for(int i=cur[u];~i&&flow0)add(S,i,A[i]),tot+=A[i];
        else if(A[i]<0)add(i,T,-A[i]);
        
    add(t,s,INF);
    if(dinic()

有源汇上下界最小流

原题链接

从$s\to t$的最小流即为$t\to s$的最大流。

①与上题一样，先建立一个$S\to T$的网络，求一遍最大流$f_0$。

②删除$t\to s$容量为$+\infty$的边。

③从$t\to s$反向求一遍最大流$f$。

④所要求的答案就为$f_0-f$。

代码如下：

#include
using namespace std;

const int N=50000+10;
const int M=400000+10;
const int INF=2147483647;

int n,m,S,T;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N],A[N];

void add(int x,int y,int z){
    ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
    ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}

bool bfs(){
    int he=0,ta=0;
    memset(d,-1,sizeof d);
    q[0]=S;d[S]=0;cur[S]=h[S];
    
    while(he<=ta){
        int x=q[he++];
        
        for(int i=h[x];~i;i=ne[i]){
            int y=ve[i];
            
            if(d[y]==-1&&c[i]){
                d[y]=d[x]+1;
                cur[y]=h[y];
                if(y==T)return true;
                q[++ta]=y;
            }
        }
    }
    
    return false;
}

int dfs(int u,int limit){
    if(u==T)return limit;
    int flow=0;
    
    for(int i=cur[u];~i&&flow0)add(S,i,A[i]),tot+=A[i];
        else if(A[i]<0)add(i,T,-A[i]);
        
    add(t,s,INF);
    
    if(dinic()

多源汇

多源汇最大流

原题链接

建图：构造一个虚拟源点$S$与一个虚拟汇点$T$，从$S$向每个源点$s_i$连一条容量为$+\infty$的边，从每个汇点$t_i$向$T$连一条容量为$+\infty$的边。

求出$S\to T$的最大流，就是原题的最大流。

证明其正确性：

证明原图的任何一个可行流都可以变成对应的新图的某一可行流，新图的任何一个可行流都可以变成对应的原图的某一可行流（即证明原图的可行流与新图的可行流一一对应），且证明它们在数值上是相等的。

①对于新图，中间的边与原图的中间的边一样，因此满足容量限制；同理中间的所有点（即除$S,T,s_i,t_i$）也都满足流量守恒。

②对于新图，左边的边流入的流量为从$s_i$流出的流量，即保证了$s_i$满足流量守恒，且左边的边也都满足容量限制。

③同理，对于右边的点与$t_i$也满足流量守恒与容量限制。

因此原图的可行流可以通过这样的方式转化为新图的一个可行流。

反之，对于新图，中间部分不用变，删去$S$与从$S$流向$s_i$的边，$T$与从$t_i$流向$T$的边，即又变成了原图。

因此新图的可行流可以通过这样的方式转化为原图的一个可行流。

代码如下：

#include
using namespace std;

const int N=10000+10;
const int M=300000+10;
const int INF=1e9;

int n,m,Sc,Tc,S,T;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N];

void add(int x,int y,int z){
    ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
    ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}

bool bfs(){
    int he=0,ta=0;
    memset(d,-1,sizeof d);
    q[0]=S;d[S]=0;cur[S]=h[S];
    
    while(he<=ta){
        int x=q[he++];
        
        for(int i=h[x];~i;i=ne[i]){
            int y=ve[i];
            
            if(d[y]==-1&&c[i]){
                d[y]=d[x]+1;
                cur[y]=h[y];
                if(y==T)return true;
                q[++ta]=y;
            }
        }
    }
    return false;
}

int dfs(int u,int limit){
    if(u==T)return limit;
    int flow=0;
    
    for(int i=cur[u];~i&&flow

关键边

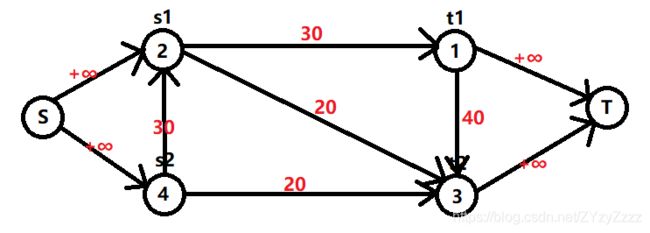
伊基的故事 I - 道路重建

原题链接

求关键边的数量。

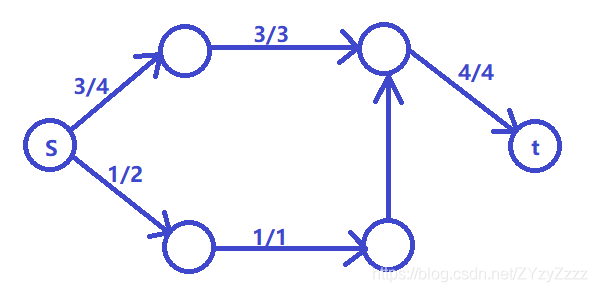
如图所建的流网络所标出的可行流为最大流。

希望在图中把一条边的容量变大，使得整个图的最大流可以变大。这条边就是关键边。

若将$4$增加到$5$：

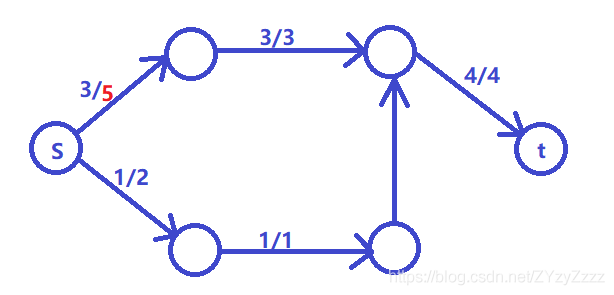
最流网络无影响，所标出的可行流依然为最大流。

若将$3$增加到$4$：

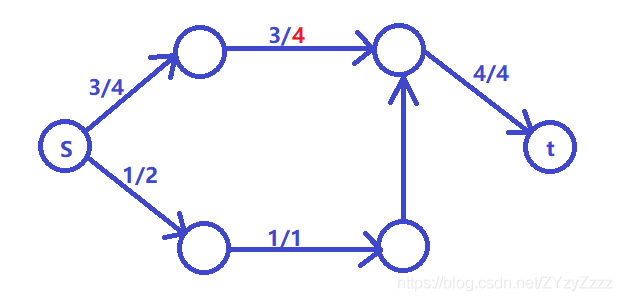
此时所标出的可行流不为流网络的最大流。

我们可以发现一个规律：我们只需要考虑改变原为满流的边就可以。

①在$G$中，求最大可行流$f$。

②若$f(u,v)<c(u,v)$，那么这条边必然不可能是关键边。

③若$f(u,v)==c(u,v)$，那么这条边才有可能是关键边。

因此，边$c(u,v)$为关键边的条件是：

①对于$G$的最大可行流$f$，$f(u,v)==c(u,v)$。

②在$Gf$中，从$S$到$u$、从$v$到$T$都存在路径（路径中所有的边的容量都大于$0$）。

代码如下：

#include
using namespace std;

const int N=500+10;
const int M=10000+10;
const int INF=1e9;

int n,m,S,T;
int h[N],ve[M],c[M],ne[M],id;
int q[N],d[N],cur[N];
bool vs[N],vt[N];

void add(int x,int y,int z){
    ve[id]=y;c[id]=z;ne[id]=h[x];h[x]=id++;
    ve[id]=x;c[id]=0;ne[id]=h[y];h[y]=id++;
}

bool bfs(){
    int he=0,ta=0;
    memset(d,-1,sizeof d);
    q[0]=S;d[S]=0;cur[S]=h[S];
    
    while(he<=ta){
        int x=q[he++];
        
        for(int i=h[x];~i;i=ne[i]){
            int y=ve[i];
            
            if(d[y]==-1&&c[i]){
                d[y]=d[x]+1;
                cur[y]=h[y];
                if(y==T)return true;
                q[++ta]=y;
            }
        }
    }
    
    return false;
}

int dfs1(int u,int limit){
    if(u==T)return limit;
    int flow=0;
    
    for(int i=cur[u];~i&&flow