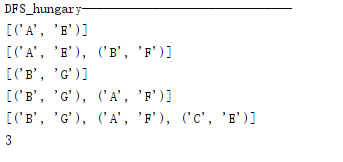python实现匈牙利算法

1.通过深度优先搜索实现匈牙利算法

#-*-coding:utf-8-*-
#created by lixiao at 2019/4/16

class DFS_hungary():

    def __init__(self, nx, ny, edge, cx, cy, visited):
        self.nx, self.ny=nx, ny   #x和y集合中顶点的个数
        self.edge = edge #edge[i][j]为1表示i，j可以匹配
        self.cx, self.cy=cx,cy #用来记录x集合中匹配的y元素是哪个
        self.visited=visited  #用来记录该顶点是否被访问过
        self.M=[]

    def match(self):
        res=0
        for i in self.nx:
            if self.cx[i]==-1:  #初始值为-1表示两个集合中都没有匹配的元素
                for key in self.ny:
                    self.visited[key]=0   # 将visited置0表示未访问过
                res+=self.path(i)
        return res

    def path(self, u):
        for v in self.ny：
            if self.edge[u][v] and (not self.visited[v]):
                self.visited[v]=1
                if (self.cy[v])==-1 :
                    self.cx[u] = v
                    self.cy[v] = u
                    self.M.append((u,v))
                    print(self.M)
                    return 1
                else:
                    self.M.remove((self.cy[v], v))
                    if self.path(self.cy[v]):
                        self.cx[u] = v
                        self.cy[v] = u
                        self.M.append((u, v))
                        print(self.M)
                        return 1
        return 0




if __name__ == '__main__':
    print("DFS_hungary------------------------------")
    nx, ny = ['A', 'B', 'C', 'D'], ['E', 'F', 'G', 'H']
    edge = {'A':{'E': 1, 'F': 1, 'G': 0, 'H':0}, 'B':{'E': 0, 'F': 1, 'G': 1, 'H':0}, 'C':{'E': 1, 'F': 1, 'G': 0, 'H':0}, 'D':{'E': 0, 'F': 0, 'G': 1, 'H':0}} # 1 表示可以匹配， 0 表示不能匹配
    cx, cy = {'A':-1,'B':-1,'C':-1,'D':-1}, {'E':-1,'F':-1,'G':-1,'H':-1}
    visited = {'E': 0, 'F': 0, 'G': 0,'H':0}

    print(DFS_hungary(nx, ny, edge, cx, cy, visited).match())

2.通过广度优先搜索实现匈牙利算法

def BFS_hungary(g,Nx,Ny,Mx,My,chk,Q,prev):
    res=0
    for i in range(Nx):
        if Mx[i]==-1:
            qs=qe=0
            Q[qe]=i
            qe+=1
            prev[i]=-1

            flag=0
            while(qs=0:
                            prev[My[v]]=u
                        else:
                            flag=1
                            d,e=u,v
                            while d!=-1:
                                t=Mx[d]
                                Mx[d]=e
                                My[e]=d
                                d=prev[d]
                                e=t
                qs+=1
            if Mx[i]!=-1:
                res+=1
    return res
if __name__ == '__main__':
       print("BFS_hungary------------------------------")
       g = [[1, 1, 0, 0], [0, 1, 1, 0], [1, 1, 0, 0], [0, 0, 1, 0]]
       Nx=4
       Ny=4
       Mx=[-1,-1,-1,-1]
       My=[-1,-1,-1,-1]
       chk=[-1,-1,-1,-1]
       Q=[0 for i in range(100)]
       prev=[0,0,0,0]
       print(BFS_hungary(g,Nx,Ny,Mx,My,chk,Q,prev))