Atcoder Grand Contest 016F - Games on DAG

 

Problem Statement

There is a directed graph G with N vertices and M edges. The vertices are numbered 1 through N, and the edges are numbered 1 through M. Edge i is directed from xi to yi. Here, xi<yi holds. Also, there are no multiple edges in G.

Consider selecting a subset of the set of the M edges in G, and removing these edges from G to obtain another graph G'. There are 2M different possible graphs as G'.

Alice and Bob play against each other in the following game played on G'. First, place two pieces on vertices 1 and 2, one on each. Then, starting from Alice, Alice and Bob alternately perform the following operation:

• Select an edge i such that there is a piece placed on vertex xi, and move the piece to vertex yi (if there are two pieces on vertex xi, only move one). The two pieces are allowed to be placed on the same vertex.

The player loses when he/she becomes unable to perform the operation. We assume that both players play optimally.

Among the 2M different possible graphs as G', how many lead to Alice's victory? Find the count modulo 109+7.

Constraints

• 2≤N≤15
• 1≤M≤N(N−1)⁄2
• 1≤xi<yi≤N
• All (xi, yi) are distinct.

---

Input

Input is given from Standard Input in the following format:

N M
x1 y1
x2 y2
:
xM yM

Output

Print the number of G' that lead to Alice's victory, modulo 109+7.

---

Sample Input 1

Copy

2 1
1 2

Sample Output 1

Copy

1

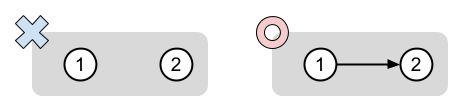
The figure below shows the two possible graphs as G'. A graph marked with ○ leads to Alice's victory, and a graph marked with × leads to Bob's victory.

---

Sample Input 2

Copy

3 3
1 2
1 3
2 3

Sample Output 2

Copy

6

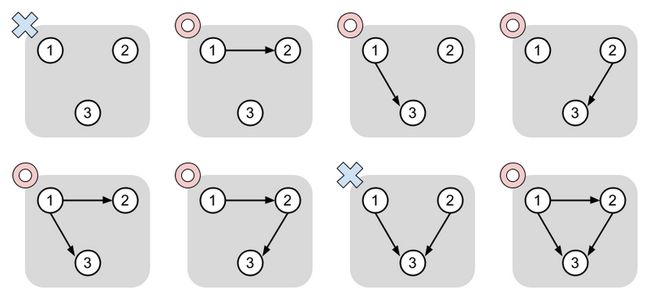
The figure below shows the eight possible graphs as G'.

---

Sample Input 3

Copy

4 2
1 3
2 4

Sample Output 3

Copy

2

---

Sample Input 4

Copy

5 10
2 4
3 4
2 5
2 3
1 2
3 5
1 3
1 5
4 5
1 4

Sample Output 4

Copy

816

 

 

 

题意：给一个DAG，点已经按照拓扑序重编号，统一有多少种边的子图使得在这个图上跑SG，sg[1]不等于sg[2]

题解：状压DP

先补集转化

然后记f[S]表示只考虑S这个点集，使得sg[1]=sg[2]的方案数，考虑怎么转移

枚举S的一个子集T，其补集为U，假设U集合的sg值都为0，而T集合都不为0，我们想想怎么转移：

U内部的边：一条都不能连

U到T的边：随便连

T到U的边：要求T中的每个顶点都有至少一条到U的边

T内部的边：就是f[T] 想想为什么：我们把f[T]对应的任意一种方案的所有数的sg值+1，就得到的f[S]的这样一种方案

 

#include 
#define xx first
#define yy second
#define mp make_pair
#define pb push_back
#define fill(x, y) memset(x, y, sizeof x)
#define copy(x, y) memcpy(x, y, sizeof x)
using namespace std;

typedef long long LL;
typedef pair < int, int > pa;

inline int read()
{
	int sc = 0, f = 1; char ch = getchar();
	while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') sc = sc * 10 + ch - '0', ch = getchar();
	return sc * f;
}

const int MAXN = 15;
const int MAXM = (1 << 15) + 5;
const int mod = 1e9 + 7;

inline void inc(int &x, int y) { x += y; if (x >= mod) x -= mod; }

int f[MAXM], table[MAXM], n, G[MAXN], m;

int main()
{
#ifdef wxh010910
	freopen("data.in", "r", stdin);
#endif
	n = read(), m = read();
	table[0] = 1; f[0] = 1;
	for (int i = 1; i <= m; i ++) table[i] = (table[i - 1] << 1) % mod;
	for (int i = 1, x, y; i <= m; i ++) x = read() - 1, y = read() - 1, G[x] |= 1 << y;
	for (int S = 1; S < (1 << n); S ++) if ((S & 1) == (S >> 1 & 1))
		for (int T = S; T; T = T - 1 & S) if ((T & 1) == (T >> 1 & 1))
		{
			int ways = 1;
			for (int i = 0; i < n; i ++) if (S >> i & 1)
			{
				if (T >> i & 1) ways = 1LL * ways * table[__builtin_popcount(G[i] & (S ^ T))] % mod;
				else ways = 1LL * ways * (table[__builtin_popcount(G[i] & T)] - 1) % mod;
			}
			inc(f[S], 1LL * f[S ^ T] * ways % mod);
		}
	return printf("%d\n", (table[m] - f[(1 << n) - 1] + mod) % mod), 0;
}