一眼望去不会。
考虑问题中的\(f(i,j)=|\sum_{p=i}^{j}a_p |\)的实际意义。
其实就是前缀和相减的绝对值。
\(f(i,j)=|\ sum[j]-sum[i-1]\ |\)
\(f(i,j)=max(sum[j]-sum[i-1],sum[i-1]-sum[j])\)
那加上x呢。
\(f(i,j)=max[(sum[j]+xj)-(sum[i-1]+x(i-1)),(sum[i-1]+x(i-1))-(sum[j]+xj)]\)
\(sum[i]+xi\)联想到直线。
我们把这些直线放到坐标系里。
(这个图是从别人那里蒯过来的)
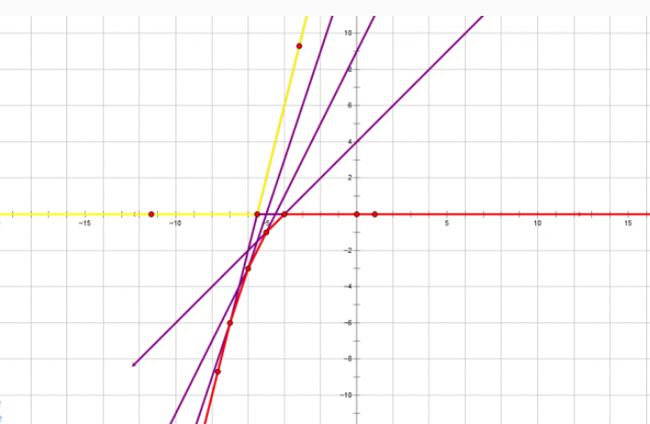
这是把样例转为坐标系中直线的效果图。
对于一个 \(x\) ,我们询问的实际上就是横坐标为x的两条直线纵坐标的差的最大值。
所以我们用半平面交的方法维护出上下两个凸包。
因为题目中的强制在线是假的(实际上处理出的\(x\in [-2n,2n]\))。
又因为凸包上的线段斜率是单调的,我们可以直接处理出所有 \(x\) 时的答案。
然后这题就解决了。
#include
#include
#include
#include
#include
#include
