【算法笔记】并查集(风险度量&通畅工程)
并查集这玩意上课老师没讲,听上去就很高大上,一看到题目说要用并查集,ψ(。。)什么!?并查集?什么玩意?算了算了,放弃这道题刷别的吧。今天研究了下并查集,发现还是挺简单的,博客上做个整理,以后忘了上来瞅瞅_(¦3」∠)_
并查集
并查集主要是用来检测两个点是否连通的,主要有两个功能,一个是find一个是join。至于什么时候用并查集,我想大概是你觉得需要判断这两个点是否连通吧,例如,几个个城市之间有几条几条路,判断其中两个城市是否连通。
①并查集的初始化
并查集一般是用一个一维数组来存储的,其中pre[i]=i表示自己和自己是连通的,也就是说还没有往点之间添加路径。
②并查集join
join主要是用来往存放并查集的一维数组中添加路径的,先判断两个点之间是否连通,如果连通就不用添加路径了,如果不连通那么将两个点的根节点连在一起。
void join(int x,int y)
{
int i,j;
i = find(x); //寻找x的根节点
j = find(y); //寻找y的根节点
if(i!=j) //如果两个根节点不同,即不连通,将根节点连在一起
pre[i] = j; //即i链接j
}③并查集find
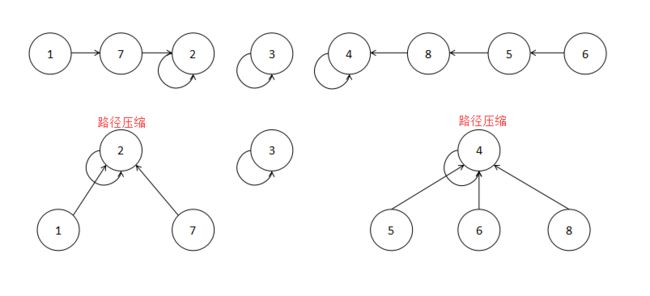
find主要有两个部分,一个是寻找根节点,一个是将路径压缩。如果两个节点的根节点是同一个,那么这两个节点一定是连通的,就像两个人的老大是同一个人,那么这两个人一定是同一个帮派的=w=
int find(int x)
{
int i = x;
while(pre[i]!=i) //查找根节点
i = pre[i];
//路径压缩
int j = x;
int k;
while(j!=i)
{
k = pre[j];
pre[j] = i;
j = k;
}
return i;
}下面有两道例题来详细讲解一下并查集的用法
蓝桥杯 历届试题 风险度量
X星系的的防卫体系包含 n 个空间站。这 n 个空间站间有 m 条通信链路,构成通信网。
两个空间站间可能直接通信,也可能通过其它空间站中转。
对于两个站点x和y (x != y), 如果能找到一个站点z,使得:
当z被破坏后,x和y无法通信,则称z为关于x,y的关键站点。
显然,对于给定的两个站点,关于它们的关键点的个数越多,通信风险越大。
你的任务是:已知网络结构,求两站点之间的通信风险度,即:它们之间的关键点的个数。
输入数据第一行包含2个整数n(2 <= n <= 1000), m(0 <= m <= 2000),分别代表站点数,链路数。
空间站的编号从1到n。通信链路用其两端的站点编号表示。
接下来m行,每行两个整数 u,v (1 <= u, v <= n; u != v)代表一条链路。
最后1行,两个数u,v,代表被询问通信风险度的两个站点。
输出:一个整数,如果询问的两点不连通则输出-1.
例如:
用户输入:
7 6
1 3
2 3
3 4
3 5
4 5
5 6
1 6
则程序应该输出:
2
#include
using namespace std;
int pre[1001];
int u[2001],v[2001];
int find(int x)
{
int i = x;
while(pre[i]!=i) //查找根节点
i = pre[i];
//路径压缩
int j = x;
int k;
while(j!=i)
{
k = pre[j];
pre[j] = i;
j = k;
}
return i;
}
void join(int x,int y)
{
int i,j;
i = find(x);
j = find(y);
if(i!=j)
pre[i] = j;
}
int main()
{
int n,m;
cin>>n>>m;
int i,x,y;
for(i=0;i>x>>y;
u[i] = x;
v[i] = y;
join(x,y);
}
cin>>x>>y;
if(find(x)!=find(y)) //如果不连通就输出-1
cout<<"-1"< 2005年浙江大学计算机复试 通畅工程 NYOJ608
畅通工程
- 描述
- 某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。问最少还需要建设多少条道路?
- 输入
-
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数,分别是城镇数目N ( < 1000 )和道路数目M;随后的M行对应M条道路,每行给出一对正整数,分别是该条道路直接连通的两个城镇的编号。为简单起见,城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时,输入结束,该用例不被处理。 - 输出
- 对每个测试用例,在1行里输出最少还需要建设的道路数目。
- 样例输入
-
4 2 1 3 4 3 3 3 1 2 1 3 2 3 5 2 1 2 3 5 999 0 0
- 样例输出
-
1 0 2 998
这个题好烦,WA了好多次最后发现是一个小小小错误,还有说我超时,把cin全部换成scanf什么的了。还有一种写法比这个感觉稍微麻烦一点点,可以了解一下。
方法一:n个站点最多有n-1个条路径使所有站点相连即total=n-1,如果一个站点i的pre[i]不等于自己本身,也就是这个站点处于一段连通的路径里面一个,所以total可以减1,判断完所有站点之后total为还需要修路的站点。
方法二:要将n个站点相连通,也就是要将每个连通路径的根节点相连通,求出根节点的数量num,最终还需要修建的路径数就为num-1。
#include
#include
using namespace std;
int pre[1005];
int find(int x)
{
int i = x;
while(pre[i]!=i)
i = pre[i];
return i;
}
int main()
{
int n,m;
int i,a,b,total,fa,fb;
while(scanf("%d",&n) && n!=0)
{
scanf("%d",&m);
total = n-1; //n个站点全部连通最少需要n-1条路径
for(i=1;i<=n;i++)
pre[i] = i;
for(i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
fa = find(a);
fb = find(b);
if(fa!=fb)
pre[fa] = fb;
}
for(i=1;i<=n;i++)
{
if(pre[i]!=i) //也就是有相连的路径
total --;
}
printf("%d\n",total);
}
return 0;
}