图论-网络流④-最大流解题①

图论-网络流④-最大流解题①

上一篇：图论-网络流③-最大流②

下一篇：图论-网络流⑤-最大流解题②

参考文献：

• https://www.luogu.com.cn/problemnew/solution/P1231

大纲

• 什么是网络流
• 最大流（最小割）

• $Dinic$ （常用）
• $EK$
• $Sap$
• $Ford-Fulkerson$（不讲）
• $HLPP$ （快）

• 最大流解题 $\text{Start}$ $\text{End}$
• 费用流

• $EK$ 费用流
• $Dinic$ 费用流
• $zkw$ 费用流

• 费用流解题

• 有上下界的网络流

• 无源汇上下界可行流
• 有源汇上下界可行流
• 有源汇上下界最大流
• 有源汇上下界最小流
• 最大权闭合子图

• 有上下界的网络流解题

上两篇讲了最大流的定义以及 $4$ 种算法，这一篇会讲最大流的解题。

最大流解题

如果某某 $Tarjan$ 算法仅用于图上，那么这个算法的题就非常单调了。幸好后来有神仙发明了$2-sat$挽救了这个算法。

同理，如果网络流只能用来计算下水管道里的东西的话，那么它就不会风靡$OI$了。所以，蒟蒻在这里放几个经典例题，来跟大家具体讲解。

[luogu原创]教辅的组成

然后你有$5$分钟的读题时间和$2$分钟的惊讶时间。

---

你拿到这题后，会吃惊：这更像$dp$题一些！如果你学过二分图（匈牙利算法），你可能就会知道——这是两个连着的二分图。

你可以这么想，一组教辅就像一条 $s\to \text{练习册}\to \text{书}\to \text{答案}$ 的路径。其中练习册和书得可能对应，书和答案也得可能对应。所以可以把书、练习册、答案先全扔地上，然后从源点向练习册连边，从答案向汇点连边，从练习册向可能对应的书连边，从书向可能对应的答案连边（流量都为$1$，如下），就有 $10$ 分了（？？？）。

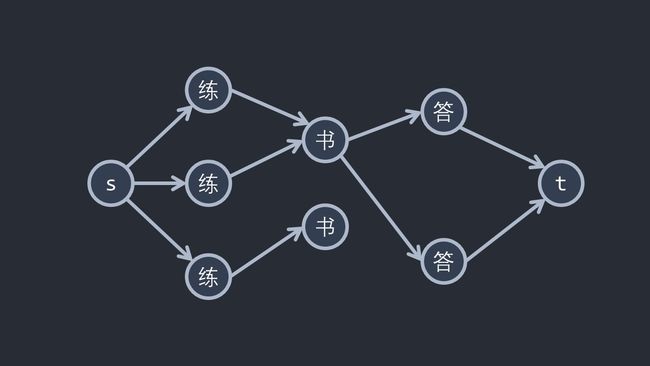
你会再次惊讶：这么完美的图哪错了呢？其实你仔细看会发现：上面图的最大流为 $2$，而你只能凑成 $1$ 套教辅。

其中的玄机是：上面那本书被用了两次！可是你不能给点设流量啊，所以大技巧出场：拆点（如下）。

把每本书拆成两本，入边连一本，出边连一本，两本间流量为 $1$，这样就相当于给点设了个流量，保证了一本书只用一遍。

整理一下：

$s\stackrel{flow=1}{}\text{每本练习册}$

$\text{每本练答案}\stackrel{flow=1}{}t$

对于每本书：

$\text{该书左半本}\stackrel{flow=1}{}\text{该书右半本}$

然后对于每个书和练习册的关系：

$\text{该练习册}\stackrel{flow=1}{}\text{该书左半本}$

然后对于每个书和答案的关系：

$\text{该书右半本}\stackrel{flow=1}{}\text{该答案}$

节点数$=2N_1+N_2+N_3+2\le 40002$，边数$=2(N_1+N_2+N_3+M_1+M_2)\le 140000$。代码：

#include 
using namespace std;
const int inf=0x3f3f3f3f;
template<int V,int M>
class Dinic{
     
public:int E,g[V],to[M],nex[M],fw[M];
	void clear(){
     memset(g,0,sizeof g),E=1;} 
	//E=1保证了互为反边的两条边可以通过^1互相得到
	Dinic(){
     clear();}
	//初始化
	void add(int x,int y,int f){
     nex[++E]=g[x],to[E]=y,fw[E]=f,g[x]=E;}
	//标准加边
	void Add(int x,int y,int f){
     add(x,y,f),add(y,x,0);}
	//加正边和反边，使得增广可以反悔
	int dep[V],cur[V];bool vis[V];queue<int> q;
	//dep表示层次，cur为单前弧优化，下面会讲。
	//vis表示是否访问，queue维护bfs
	bool bfs(int s,int t,int p){
     
		for(int i=1;i<=p;i++) vis[i]=0,cur[i]=g[i];
		q.push(s),vis[s]=1,dep[s]=0; //从源点开始bfs
		while(q.size()){
     
			int x=q.front();q.pop();
			for(int i=g[x];i;i=nex[i])if(!vis[to[i]]&&fw[i])
				q.push(to[i]),vis[to[i]]=1,dep[to[i]]=dep[x]+1;
				//bfs过程中顺便给每个节点标上层次。
		}
		return vis[t]; //表示联通
	}
	int dfs(int x,int t,int F){
     
		if(x==t||!F) return F;
		int f,flow=0;
		for(int&i=cur[x];i;i=nex[i]) //即i=g[x]
			if(dep[to[i]]==dep[x]+1&&(f=dfs(to[i],t,min(F,fw[i])))>0) //沿着层次增广
				{
     fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F) break;}
				//边的流量调整
		return flow; //一次增广的流量。
	}
	int dinic(int s,int t,int p){
      //多次增广函数
		int res=0,f;
		while(bfs(s,t,p)) while((f=dfs(s,t,inf))) res+=f;
		return res;
	}
};
int n1,n2,n3,m1,m2,s,t,p;
Dinic<40010,140010> net;
int main(){
     
	scanf("%d%d%d",&n1,&n2,&n3);
	p=t=n1*2+n2+n3+2,s=t-1;
	for(int i=1;i<=n2;i++)
		net.Add(s,i+n1*2,1);
	for(int i=1;i<=n3;i++)
		net.Add(i+n1*2+n2,t,1);
	for(int i=1;i<=n1;i++)
		net.Add(i,i+n1,1);
	scanf("%d",&m1);
	for(int i=1,x,y;i<=m1;i++){
     
		scanf("%d%d",&x,&y);
		net.Add(y+n1*2,x,1);
	}
	scanf("%d",&m2);
	for(int i=1,x,y;i<=m2;i++){
     
		scanf("%d%d",&x,&y);
		net.Add(x+n1,y+n1*2+n2,1);
	}
	printf("%d\n",net.dinic(s,t,p));
	return 0;
}

总结：此题做法是拆点$+$最大流

你做完这道题后，想必对网络流的解题方法有了些了解，那么看下面这道例题：

[网络流24题]骑士共存问题

然后你有$5$分钟的读题时间和$2$分钟的谔谔时间。

---

这题自己做估计能消耗一个下午，但这题是经典中的经典。假设你思考过了，我就开始讲题了：

我自己以前写的题解：题解 P3355 【骑士共存问题】

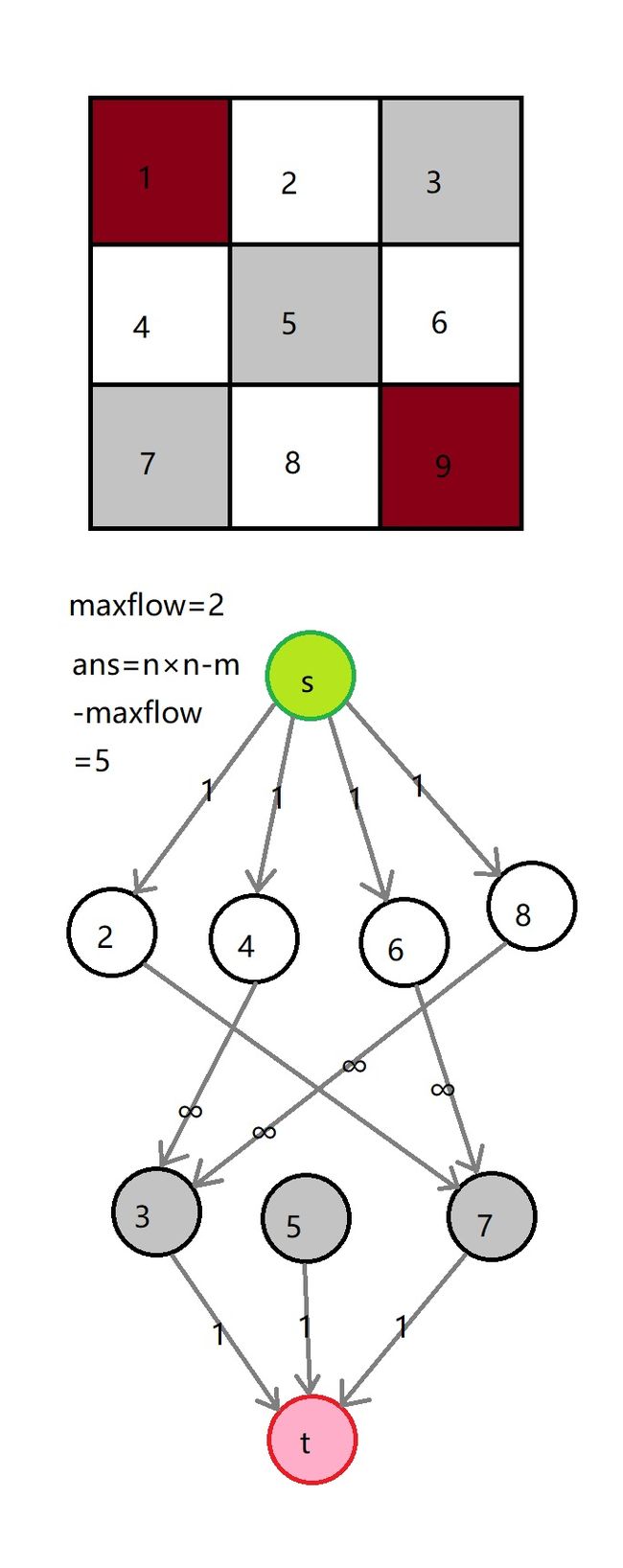
先将格图黑白间隔染色，由于一只骑士能攻击到的骑士在与自己异色的格中，有一种摆法是都摆白格子上或黑格子上。所以先将能放骑士的地方都放上，然后把扔掉最少骑士化为求最小割问题。

因为有矛盾的骑士只能放一个，所以先$s$ 向每个白格点连流量为 $1$ 的边，每个黑格点向 $t$ 连流量为 $1$ 的边，然后把一条互相攻击的关系变为网络流路径，流量为 $\infty$，然后求最小割 。答案是总共能放的骑士数$-$网络流最小割。如下图：

代码（以前写的，码风很蒻）：

#include 
using namespace std;
const int N=2e5+10; //n方大小
const int M=2e6+10; //10n方大小
const int inf=1e8+10;
int n,m,s,t,ans;
struct edge{
     
    int adj,nex,fw;
}e[M];
int g[N],top=1;
void add(int x,int y,int z){
     
    e[++top]=(edge){
     y,g[x],z};
    g[x]=top;
}
//以下是最大流模板，每道题都一样
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool bfs(){
     
    for(int i=1;i<=n;i++)
        vis[i]=0,cur[i]=g[i];
    Q.push(s),vis[s]=1,dep[s]=0;
    while(Q.size()){
     
        int x=Q.front(); Q.pop();
        for(int i=g[x];i;i=e[i].nex){
     
            int to=e[i].adj;
            if(!vis[to]&&e[i].fw){
     
                vis[to]=1;
                dep[to]=dep[x]+1;
                Q.push(to);
            }
        }
    }
    return vis[t];
}
int dfs(int x,int F){
     
    if(!F||x==t)
        return F;
    int flow=0,f;
    for(int i=cur[x];i;i=e[i].nex){
     
        int to=e[i].adj; cur[x]=i;
        if(dep[x]+1==dep[to]&&
        (f=dfs(to,min(F,e[i].fw)))>0){
     
            e[i].fw-=f;
            e[i^1].fw+=f;
            flow+=f,F-=f;
            if(!F) break;
        }
    }
    return flow;
}
int p(int x,int y){
     return (x-1)*n+y;} //给点编号
bool G[210][210]; //1表示障碍，0表示可放骑士
int tx[]={
     1,1,2,2,-1,-1,-2,-2};
int ty[]={
     -2,2,-1,1,-2,2,-1,1}; //攻击方向
int main(){
     
    scanf("%d%d",&n,&m);
    for(int i=1,x,y;i<=m;i++){
     
        scanf("%d%d",&x,&y);
        G[x][y]=1;
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++){
     
            if(G[i][j]) continue;
            if((i+j)&1){
      //白格子
                add(1,p(i,j)+1,1);
                add(p(i,j)+1,1,0);
                for(int k=0;k<8;k++){
     
                    int xt=tx[k]+i,yt=ty[k]+j;
                    if(xt<1||xt>n||yt<1||yt>n||G[xt][yt])
                        continue;
                    add(p(i,j)+1,p(xt,yt)+1,inf);
                    add(p(xt,yt)+1,p(i,j)+1,0);
                }
            } else add(p(i,j)+1,n*n+2,1), //黑格子
                add(n*n+2,p(i,j)+1,0);
        }
    ans=n*n-m,s=1,n=t=n*n+2; //将ans初始化，将n变为网络流节点数
    while(bfs()) ans-=dfs(s,inf); //网络流模板
    printf("%d\n",ans);
    return 0;
}

总结：做题要双向思考。这题中用到了要把求能放几个转化为最少扔几个，把最大流题转化为最小割。

下一篇会讲最大流解题的进阶。

祝大家学习愉快！